Author: Denis Avetisyan
Researchers are exploring how techniques from the world of polar codes can be applied to improve the decoding of Reed-Solomon codes, a cornerstone of data storage and transmission.
This review analyzes the performance of successive cancellation list decoding for extended Reed-Solomon codes transformed into binary polar codes, highlighting trade-offs with increasing codeword length.
Achieving robust and efficient decoding for non-binary codes remains a challenge despite their prevalence in modern communication and data storage. This is addressed in ‘Successive Cancellation List Decoding of Extended Reed-Solomon Codes’, which proposes a novel decoding approach for extended Reed-Solomon codes by transforming them into binary polar codes. This transformation enables the application of successive cancellation (SC) and successive cancellation list (SCL) decoding, with theoretical analysis revealing performance limitations related to codeword length and matrix properties. Does this binary reinterpretation offer a viable pathway toward practical, high-performance decoding of non-binary codes, particularly for shorter block lengths where implementation complexity is less prohibitive?
The Inherent Limitations of Traditional Error Correction
While error-correcting codes such as Reed-Solomon have long been the cornerstone of reliable data transmission – effectively safeguarding information across CDs, DVDs, and deep-space communications – their performance begins to degrade when confronted with the nuanced challenges of contemporary communication channels. These codes were initially designed assuming relatively simple error models, primarily random bit flips; however, modern signals often encounter more complex distortions, including burst errors caused by fading, interference, and impulsive noise. As data rates escalate and channels become increasingly congested, the probability of these complex errors rises, overwhelming the capabilities of traditional binary-based approaches. Consequently, the very systems designed to ensure data integrity find themselves struggling to maintain reliability in the face of increasingly sophisticated channel impairments, necessitating a shift towards more adaptive and robust error correction strategies.
Although Reed-Solomon codes and similar error-correcting methods demonstrate considerable robustness, their practical application is often hampered by the computational demands of decoding. Algorithms such as the Berlekamp-Massey algorithm, essential for recovering data, exhibit a complexity that scales rapidly with increasing data rates and the degree of error correction required. This means that as communication speeds rise and channels become more unreliable, the processing power needed to decode data accurately grows exponentially, creating a significant bottleneck in systems demanding real-time performance. The intensive calculations involved not only strain hardware resources but also contribute to increased energy consumption, limiting the scalability and feasibility of these traditional codes in modern, high-bandwidth applications.
Conventional error correction frequently relies on binary principles, representing information as 0s and 1s, a system that, while foundational, presents escalating challenges in modern data transmission. As data rates surge and communication channels become increasingly complex-introducing non-binary noise and interference-the computational demands of decoding binary codes, such as those employing the Berlekamp-Massey algorithm, become prohibitive. This inherent scalability issue drives research toward alternatives like non-binary Low-Density Parity-Check (LDPC) codes and fountain codes, which offer the potential for significantly improved efficiency and reduced complexity. These approaches leverage larger symbol alphabets, enabling more compact representations of data and the creation of codes inherently better suited to the demands of high-throughput, reliable communication in the digital age, ultimately promising systems that can adapt and scale more effectively than their binary counterparts.
Polar Codes: A Paradigm Shift in Efficient Communication
Polar codes represent a class of error-correcting codes that are provably capacity-achieving, meaning they can reliably transmit data at rates approaching the Shannon limit of a given communication channel. This capability stems from a technique called channel polarization, which transforms the original binary discrete memoryless channel (BPMC) into a set of synthesized channels. These synthesized channels exhibit drastically different properties; some become nearly noiseless, ideal for transmitting information, while others become highly noisy and are therefore assigned to frozen bits – predetermined bits known to both the encoder and decoder. By systematically assigning information bits to the reliable channels and frozen bits to the unreliable ones, polar codes achieve performance comparable to the best known codes while offering a lower complexity decoding process, particularly with the Successive Cancellation List Decoding algorithm. The capacity-achieving property is formally demonstrated through the polarization phenomenon, where the error probability of the synthesized channels converges to either zero or one as the code length increases.
Polar code construction frequently incorporates Extended Binary Cyclic (BCH) codes as fundamental building blocks, enabling a degree of flexibility in managing “frozen” bits – pre-defined bits with known values used for decoding. These BCH codes provide a structured approach to generating the polar code’s parity-check matrix, influencing the code’s error-correcting capabilities. The use of Extended BCH codes facilitates dynamic control over the placement of frozen bits, allowing designers to optimize the code structure for specific channel conditions and desired performance metrics, such as block length and decoding complexity. This dynamic control is crucial for adapting polar codes to diverse communication scenarios and maximizing their efficiency.
Successive Cancellation List Decoding (SCLD) is a decoding algorithm for polar codes that improves upon standard Successive Cancellation (SC) decoding by maintaining a list of the L most likely candidate codewords at each stage. Unlike SC decoding, which commits to a single path early in the process, SCLD postpones hard decisions, allowing for error correction based on the cumulative probabilities of multiple potential solutions. The algorithm operates by iteratively processing the bit-channels, and at each stage, it expands the list of candidate codewords by considering all possible values for the current bit. Pruning techniques are often employed to limit the list size and computational complexity. Performance gains are achieved by effectively searching a larger portion of the decoding tree, particularly beneficial in scenarios with high signal-to-noise ratios or when dealing with imperfect channel state information. The complexity of SCLD is directly related to the list size L , making it a trade-off between decoding performance and computational resources.
Extending the Framework: Non-Binary Polar Codes
Non-binary polar codes represent an extension of classic polar coding, initially defined over the binary field GF(2), to finite fields GF(2^m). This generalization allows for the construction of codes with larger alphabet sizes, which can improve performance in certain communication scenarios. Specifically, utilizing finite fields enables the creation of codes better suited for channels where symbol errors are more costly than bit errors, or where higher-order modulation schemes are employed. The advantages stem from the ability to represent multiple bits per channel use, increasing spectral efficiency and potentially reducing the overall error rate compared to binary polar codes in those specific contexts. This approach enables the design of codes tailored to address the limitations of binary codes in complex communication systems.
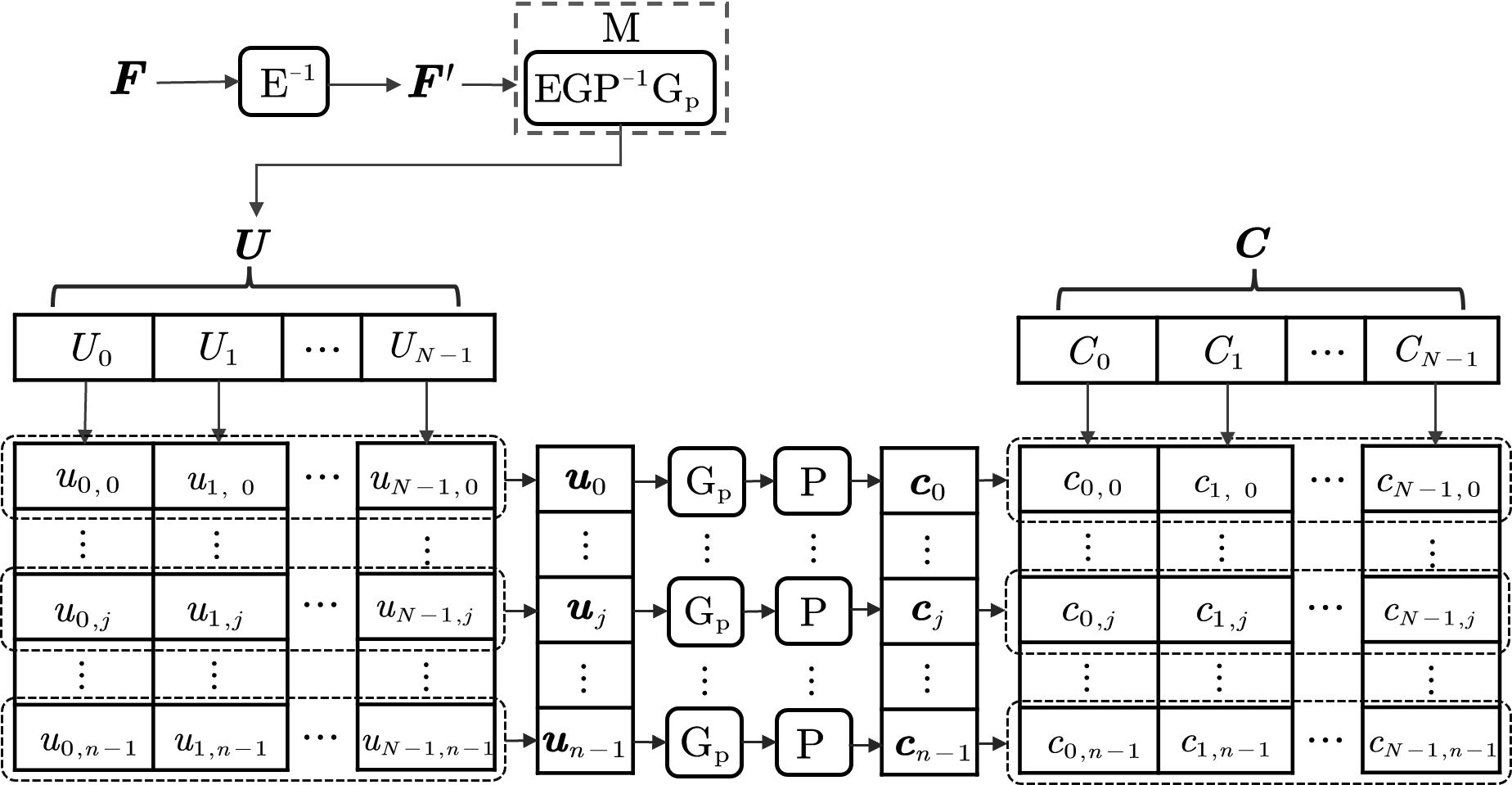
Conversion of existing codes, such as eRS codes, into a polar code structure necessitates the application of a pre-transformed matrix. This matrix performs a linear transformation on the input data, effectively rearranging the information bits to align with the requirements of polar decoding. The pre-transformed matrix is designed to ensure that the resulting code possesses the necessary properties for efficient successive cancellation (SC) decoding, specifically by creating a layered structure where dependencies between bits are minimized. The specific construction of this matrix is crucial for maintaining the code’s error correction capabilities and achieving optimal performance; without proper transformation, the benefits of polar decoding cannot be fully realized.
Successive Cancellation (SC) decoding, originally developed for polar codes, can be adapted for decoding Reed-Solomon (RS) codes following a pre-transformation into a polar-like structure. This approach utilizes the layered structure inherent in the transformed RS code to iteratively decode bit sequences, mirroring the SC decoding process. By combining the error-correcting capabilities of RS codes with the efficient decoding algorithm of polar codes, this method aims to improve decoding performance and reduce complexity in certain communication systems. The benefits of both approaches are leveraged: the strong algebraic properties of RS codes and the low-complexity decoding offered by SC decoding, resulting in a potentially more efficient decoding solution than traditional RS decoding algorithms.
System performance is demonstrably affected by the characteristics of the communication channel. Simulations conducted using an Additive White Gaussian Noise (AWGN) channel demonstrate the feasibility of decoding eRS codes utilizing Successive Cancellation (SC) decoding, a technique central to polar coding. These results indicate that the application of polar-based SC decoding to eRS codes is channel-dependent; while successful decoding was observed under specific AWGN conditions, performance will vary with differing channel impairments and noise levels. This suggests that adaptive decoding strategies or channel-aware code construction may be necessary to optimize the system for diverse communication environments.
Optimizing Performance: Algorithms and Refinements
Reed-Solomon codes, renowned for their error-correcting capabilities, can achieve even greater reliability through the implementation of advanced decoding techniques such as the Kötter-Vardy Algorithm. This iterative algorithm efficiently decodes generalized concatenated codes, including many Reed-Solomon variants, by breaking down the decoding process into smaller, more manageable steps. The Kötter-Vardy approach excels in scenarios with high noise levels or significant data corruption, offering a robust solution for recovering information that would otherwise be lost. By strategically leveraging the code’s structure, the algorithm minimizes computational complexity while maximizing the probability of successful decoding, making it a valuable tool in diverse applications like data storage, wireless communication, and deep-space exploration where data integrity is paramount.
Sequential decoding offers a compelling alternative to traditional Reed-Solomon (RS) code decoding methods by prioritizing adaptability and reduced complexity in certain scenarios. Unlike algorithms requiring exhaustive searches, sequential decoding operates by iteratively building a valid codeword, making tentative decisions about each symbol and backtracking when errors are detected. This approach allows the decoder to terminate upon finding the first valid solution, potentially reducing computational burden, especially for shorter block lengths or scenarios with low noise levels. Furthermore, sequential decoding’s inherent flexibility enables it to be easily tailored to various RS code parameters and noise characteristics, making it a valuable tool where computational resources are constrained or real-time performance is critical. While not always the most efficient method in all conditions, its ability to dynamically adjust to the decoding process presents a significant advantage in practical applications.
The selection of a modulation scheme is a critical factor influencing the overall performance of a communication system, with Binary Phase-Shift Keying (BPSK) representing a frequently employed choice due to its simplicity and robustness. BPSK achieves this by representing data as two distinct phases of a carrier signal, minimizing the impact of noise and interference. However, the efficiency of BPSK, and indeed any modulation scheme, is intrinsically linked to the channel characteristics and the decoding algorithms employed; a carefully chosen modulation scheme maximizes the reliability of transmitted information by optimizing the signal-to-noise ratio and minimizing bit errors, ultimately contributing to a more stable and efficient communication link. Consequently, systems designers must consider the interplay between modulation, channel conditions, and decoding strategies to achieve peak performance and ensure data integrity.
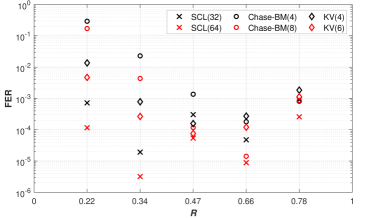
Efficient distribution of information bits within polar codes is significantly improved through the strategic employment of permutation matrices. Recent investigations demonstrate that, for length-32 erasure-correcting Reed-Solomon (eRS) codes, Successive Cancellation List (SCL) decoding consistently outperforms both the Kötter-Vardy (KV) algorithm and Chase-BM decoding. Although SCL decoding necessitates a greater computational load, measured in floating-point operations (FLOPs), the resulting Frame Error Rate (FER) performance is notably superior. Furthermore, analyses reveal that, for specific code lengths – notably (32, 15) – this approach can actually reduce the total number of operations required within the \mathbb{F}_{2^{5}} field, highlighting a compelling trade-off between computational complexity and decoding reliability.
Successive Cancellation List (SCL) decoding, despite its computational intensity measured in FLOPs, demonstrably achieves superior Frame Error Rate (FER) performance compared to algorithms like Kötter-Vardy and Chase-BM decoding. This improved reliability doesn’t necessarily equate to increased overall computational burden; for specific code lengths, notably (32, 15), careful implementation of SCL decoding can actually reduce the number of field operations within \mathbb{F}_{2^{5}} and the total FLOP count. This efficiency stems from the algorithm’s ability to explore multiple decoding candidates in parallel, effectively trading computational resources for a lower probability of decoding errors and, in certain scenarios, a more streamlined operational profile.
The pursuit of efficient decoding, as demonstrated in the analysis of extended Reed-Solomon codes, echoes a fundamental principle: algorithmic elegance transcends implementation. This work meticulously transforms a non-binary challenge into a binary framework, seeking provable performance bounds through successive cancellation list decoding. As Tim Berners-Lee stated, “The Web is more a social creation than a technical one.” Similarly, the effectiveness of these decoding methods isn’t solely about the code itself, but how it interacts with the inherent structure of information and the limits of reliable transmission. The study’s exploration of performance limitations with increasing codeword length highlights the importance of mathematical rigor in evaluating practical systems – a solution’s correctness isn’t simply determined by successful tests, but by its adherence to provable principles.
Beyond the List
The pursuit of efficient decoding for non-binary codes, as exemplified by this work on extended Reed-Solomon codes, inevitably encounters the limitations inherent in attempting to map complex structures onto the comparatively simple framework of binary polar codes. The demonstrated performance plateau with increasing codeword length is not a surprising outcome, but rather a consequence of forcing a square peg into a round hole. While successive cancellation list decoding offers a pragmatic approach, it does not address the fundamental question of whether this transformation truly unlocks the theoretical benefits of channel polarization in the non-binary domain.
Future investigations should, therefore, move beyond mere adaptation. The elegance of a code lies not in its ability to be made to resemble another, but in its intrinsic mathematical properties. Direct decoding algorithms, designed specifically for the algebraic structure of non-binary codes, represent a more promising, though undoubtedly more challenging, path. Simplicity, in this context, does not mean brevity of implementation – it means logical completeness, a solution free from the contradictions born of forced analogy.
Ultimately, the true measure of progress will not be incremental gains in decoding performance, but a deeper understanding of the fundamental limits imposed by the channel itself, and the development of codes that approach those limits with mathematical certainty, not merely empirical observation.
Original article: https://arxiv.org/pdf/2601.22482.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Gold Rate Forecast
- How to Unlock the Mines in Cookie Run: Kingdom
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
- Most Underrated Loot Spots On Dam Battlegrounds In ARC Raiders
- Gears of War: E-Day Returning Weapon Wish List
- The Saddest Deaths In Demon Slayer
- Jujutsu: Zero Codes (December 2025)
- Respawn Confirms Star Wars Jedi 3 is Still Alive!
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- Epic Pokemon Creations in Spore That Will Blow Your Mind!
2026-02-03 01:18