Decoding the Past: Reconstructing Data from Noisy Channels

by

Author: Denis Avetisyan

A new algorithm efficiently recovers Reed-Solomon codes from multiple, imperfect readings, offering a path to more reliable data storage and transmission.

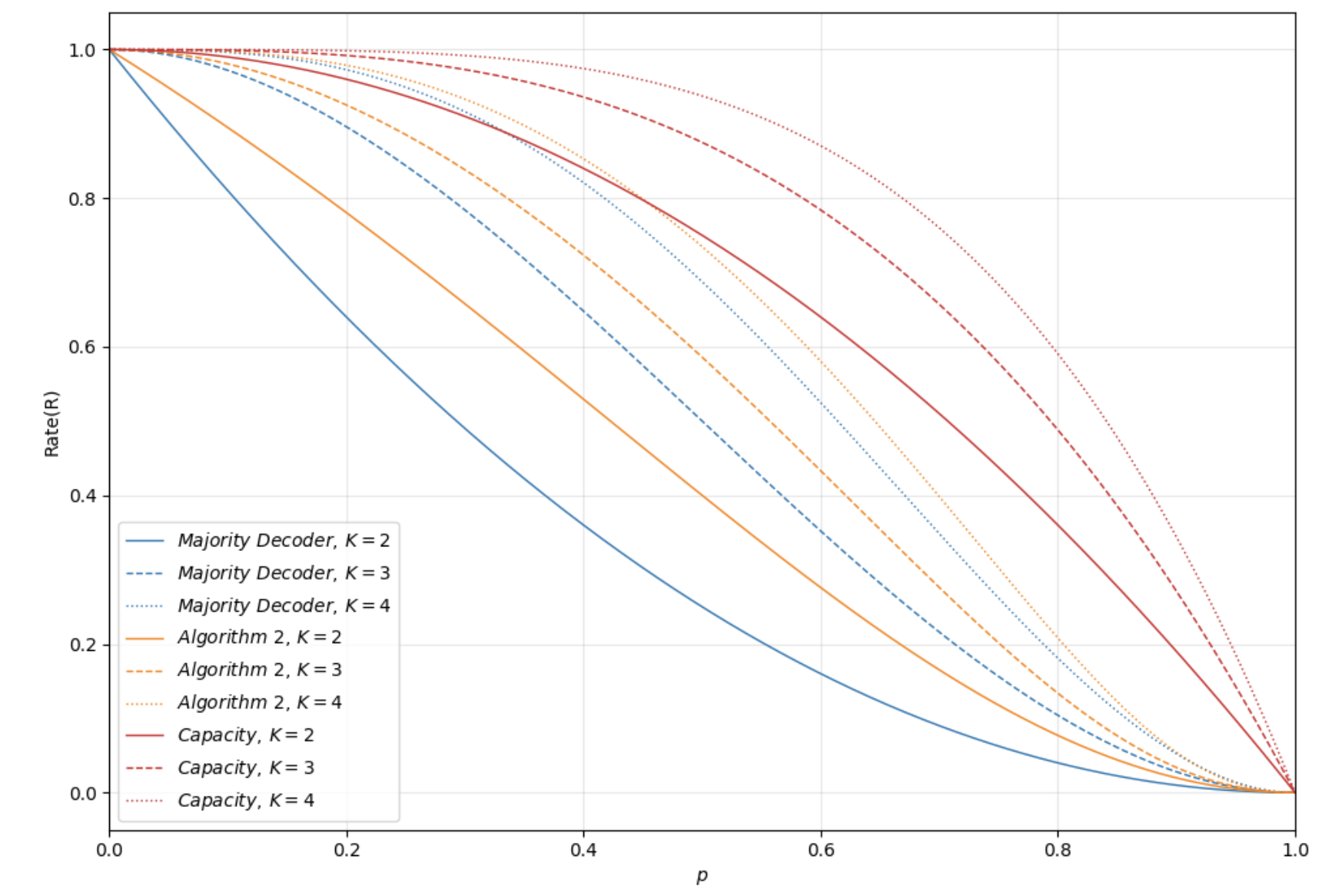
For <span class="katex-eq" data-katex-display="false"> K = 2 </span>, <span class="katex-eq" data-katex-display="false"> K = 3 </span>, and <span class="katex-eq" data-katex-display="false"> K = 4 </span>, the achievable rate regions of Algorithm 2-as established by Theorem 4-demonstrate performance approaching channel capacity (Theorem 2), surpassing that of a hard-decision majority-decoder (Corollary 2).
For K = 2 , K = 3 , and K = 4 , the achievable rate regions of Algorithm 2-as established by Theorem 4-demonstrate performance approaching channel capacity (Theorem 2), surpassing that of a hard-decision majority-decoder (Corollary 2).

Researchers demonstrate a polynomial-time reconstruction method for RS codes over discrete memoryless symmetric channels using soft-decision decoding and a novel multiplicity matrix construction.

Reliable data recovery from noisy sources remains a fundamental challenge in information theory, particularly when faced with multiple imperfect observations. This is addressed in ‘Reconstructing Reed-Solomon Codes from Multiple Noisy Channel Outputs’, which investigates efficient codeword reconstruction from K noisy channel outputs. The paper adapts a soft-decision decoding algorithm to establish a rate threshold-dependent on channel noise and observation multiplicity-below which reliable reconstruction of Reed-Solomon codes is guaranteed. Could this approach be extended to other error-correcting codes and more complex noise models, paving the way for robust data storage and transmission systems?

The Challenge of Sequence Reconstruction

The core of reliable communication often hinges on solving the Sequence Reconstruction Problem, a formidable challenge where a complete signal must be recovered from incomplete or corrupted data. Imagine a message broken into pieces, with some fragments lost during transmission or altered by interference-the receiver must then intelligently reassemble these pieces, discerning the original intent despite the imperfections. This isn’t merely a technological hurdle; it’s a fundamental constraint inherent in any communication system, be it digital data transfer, biological signaling, or even human language. The difficulty stems from the inherent ambiguity: multiple sequences can potentially explain the received fragments, and determining the correct one requires sophisticated strategies that go beyond simply identifying the most frequent patterns. Successfully addressing this problem isn’t just about minimizing errors; it’s about maximizing the information that can be reliably conveyed, even under adverse conditions.

Conventional decoding methods frequently employ a “hard-decision” strategy, treating received signals as definitively correct or incorrect without considering the degree of confidence in each bit. This simplification, while computationally efficient, discards crucial information about transmission errors; a signal flagged as ‘1’ is accepted outright, ignoring the possibility it might be a degraded or partially-corrupted representation. Consequently, performance is limited, especially in environments with significant noise or interference, as the system lacks the capacity to leverage partial information or correct likely errors. Instead of acknowledging uncertainty, hard-decision decoding effectively throws away potentially valuable data, hindering the ability to reconstruct the original signal accurately – a significant drawback when dealing with imperfect communication channels.

Establishing the absolute limits of reliable data reconstruction remains a core challenge in information theory, a pursuit significantly advanced by the pioneering work of Levenshtein, who formalized the concept of edit distance – the minimum number of operations needed to transform one sequence into another. However, theoretical bounds, while essential for understanding what is possible, often fall short of providing solutions for real-world applications. Bridging this gap requires the development of practical algorithms capable of approaching these theoretical limits despite the complexities of noisy channels and imperfect data. These algorithms must efficiently balance the need for accurate reconstruction with the computational cost of processing fragmented and potentially corrupted signals, ultimately determining the feasibility of reliable communication in various contexts.

Leveraging Probabilistic Decoding for Enhanced Reliability

Traditional hard-decision decoding assigns a single value to each received symbol, effectively discarding any ambiguity introduced by noise. In contrast, soft-decision decoding leverages the inherent probabilistic nature of communication channels by considering a range of possible values for each symbol, weighted by their likelihood. This is typically achieved by examining channel statistics and signal characteristics to determine a probability distribution for each received symbol. By incorporating this probabilistic information into the decoding process, soft-decision decoders are able to mitigate the effects of noise and interference, resulting in a demonstrably improved bit error rate compared to hard-decision schemes, particularly at lower signal-to-noise ratios. The increased complexity of soft-decision decoding is offset by this gain in reliability and performance.

Koetter-Vardy decoding enhances error correction by representing the reliability of received symbols through multiplicity matrices. These matrices, denoted as H, are constructed based on the parity-check matrix of the code and the received data. Each column of H corresponds to a symbol, and the entries indicate the relationships between that symbol and the parity checks. By analyzing these relationships, the decoder can determine the most likely transmitted codeword, even with noisy or incomplete data. The technique effectively transforms the decoding problem into a system of linear equations, solvable through standard methods like Gaussian elimination, but crucially incorporates the probabilistic information captured within the multiplicity matrix to improve accuracy and performance compared to hard-decision decoding.

Effective construction of multiplicity matrices is central to Koetter-Vardy decoding, as these matrices directly encode the reliability information gleaned from received data. Algorithm 1 provides a structured method for generating these matrices; it processes the received symbols and, based on their associated probabilities, determines the appropriate entries within the multiplicity matrix. This process involves analyzing the received data to identify potential errors and representing the relationships between symbols to facilitate error correction. The resulting matrix then serves as the foundation for the decoding process, enabling the reconstruction of the original transmitted data by leveraging the encoded symbol reliabilities.

Algorithm 2: Optimized Reconstruction via Koetter-Vardy

Algorithm 2 employs Koetter-Vardy decoding in conjunction with a pre-computed multiplicity matrix to enable robust sequence reconstruction despite data transmission errors. The multiplicity matrix defines the relationships between the transmitted symbols and the received parity checks, allowing the decoder to identify and correct errors without requiring exact matching of received data to transmitted data. This approach contrasts with simpler decoding methods by fully leveraging the redundancy introduced through the coding scheme. Specifically, the algorithm iteratively resolves inconsistencies between received signals and the parity checks defined by the multiplicity matrix, ultimately converging on the most likely transmitted sequence. This process effectively mitigates the impact of channel noise and ensures reliable reconstruction of the original data.

The KK-Draw Discrete Memoryless Channel (DMS) is a widely used model for analyzing communication systems subject to noise. In this model, K independent copies of a signal are transmitted, and the receiver randomly draws one copy to decode. This introduces a probabilistic element reflecting potential signal loss or interference. The channel is characterized by the probability p of drawing the correct copy, with 1-p representing the probability of drawing an incorrect one. Algorithm 2 is specifically designed to perform optimally within this KK-Draw DMS framework, taking advantage of the redundancy introduced by the multiple signal copies to mitigate the effects of noise and achieve reliable reconstruction, provided the coding rate adheres to the defined Rate Threshold.

The performance of the Koetter-Vardy based reconstruction algorithm is directly linked to the probabilistic noise model of the communication channel. Reliable sequence reconstruction is guaranteed only when the coding rate, denoted as R, remains below a defined Rate Threshold. This threshold is mathematically expressed as R \le K(1-p^K-(K-1)(1-p)p^(K-1))^2 / (1+(K-1)(1-p^K-K(1-p)p^(K-1))) , where K represents the number of parity symbols and p is the probability of bit error. Exceeding this rate threshold introduces an unacceptable error rate, rendering reconstruction unreliable; therefore, the coding rate must be carefully selected in relation to the channel’s noise characteristics to ensure successful data recovery.

Traditional hard-decision decoding methods categorize received signals as either correct or incorrect, discarding any probabilistic information contained within the signal itself. In contrast, Algorithm 2 employs a soft-decision approach, leveraging the full spectrum of received signal values. This is achieved by considering the magnitude and phase of the received signals, which represent the probability of a transmitted symbol being correct. By incorporating this probabilistic information, Algorithm 2 reduces the likelihood of error propagation and improves the accuracy of sequence reconstruction, particularly in noisy communication channels. This full utilization of received data allows for more robust decoding compared to methods that rely solely on binary decisions.

Demonstrating Robustness and Approaching Theoretical Limits

Algorithm 2 underwent a detailed robustness assessment utilizing a Bounded Adversarial Substitution Model, a method designed to rigorously test performance under worst-case channel conditions. This approach moves beyond simple error rate calculations by allowing for strategic, yet bounded, alterations to the transmitted signal, simulating a particularly challenging adversarial environment. By analyzing the algorithm’s behavior within this framework, researchers could confidently determine the limits of its resilience and identify potential failure points. The model’s controlled perturbations provided valuable insights into how effectively Algorithm 2 maintains accurate information transfer even when faced with intelligently crafted noise, ultimately demonstrating its capacity to perform reliably in demanding communication scenarios.

The efficacy of Algorithm 2 is underscored by its demonstrated capacity to nearly achieve the theoretical limit of information transfer over a given channel. This performance, rigorously established through a Bounded Adversarial Substitution Model, signifies that the algorithm efficiently utilizes available bandwidth and minimizes data loss. By approaching channel capacity – the maximum rate at which information can be reliably transmitted – the algorithm maximizes throughput and ensures efficient communication, even in the presence of noise or interference. This near-optimal performance highlights the algorithm’s potential for practical applications demanding high reliability and data rates, effectively pushing the boundaries of efficient information conveyance across communication channels.

The reliance of this algorithm on the Discrete Memoryless Symmetric (DMS) Channel model isn’t merely a simplifying assumption, but a crucial element underpinning its theoretical guarantees. The DMS channel, characterized by symmetry in the conditional probabilities of transmitting each symbol, allows for a rigorous mathematical treatment of channel capacity and the limits of reliable communication. By framing the analysis within this well-defined model, researchers can precisely determine the maximum rate at which information can be transmitted with arbitrarily low error. This framework facilitates the derivation of performance bounds and provides a solid basis for understanding the algorithm’s behavior under various noise conditions. Furthermore, the DMS model’s inherent structure enables the application of powerful information-theoretic tools, leading to demonstrable improvements in reconstruction reliability, particularly when the channel error probability p remains below a certain threshold related to the code length K.

A central contribution of this work is a polynomial-time algorithm designed to reliably reconstruct Reed-Solomon (RS) codewords, even when subjected to noise during transmission. The algorithm guarantees an arbitrarily small error probability – effectively ensuring perfect reconstruction – under specific conditions related to the channel’s characteristics. Specifically, reliable reconstruction is achieved when the channel parameter, denoted as ‘p’ (representing the probability of error), is less than or equal to K^{-1/(K-1)}, where ‘K’ signifies the number of redundancy symbols added to the original message. This threshold demonstrates a clear boundary for successful decoding and provides a quantifiable measure of the algorithm’s robustness against channel noise, representing a significant advancement in the field of error-correcting codes.

The pursuit of robust sequence reconstruction, as demonstrated in this work on Reed-Solomon codes, highlights a fundamental principle of system design: elegance through simplicity. The algorithm’s efficiency stems not from complex maneuvers, but from a carefully constructed multiplicity matrix enabling reliable recovery from noisy data. This echoes Marvin Minsky’s observation: “If a design feels clever, it’s probably fragile.” A robust system, like the one detailed here employing soft-decision decoding and building upon the Koetter-Vardy algorithm, prioritizes structural integrity and clarity over intricate, potentially unstable solutions. The focus on a polynomial-time reconstruction underscores the value of efficiency gained through a well-defined, understandable architecture.

The Road Ahead

The presented work establishes a clear, if exacting, price for resilience. Recovering data from imperfect channels, even with the elegant structure of Reed-Solomon codes, demands a careful accounting of dependencies. The multiplicity matrix, while effective, is not a free lunch; each additional read, each redundancy introduced, adds to the systemic cost. This suggests a future where decoding algorithms are less about brute force correction and more about efficient dependency management – minimizing the overhead required to achieve a given level of reliability.

The current framework operates within the confines of polynomial-time reconstruction, a constraint that, while practical, may obscure optimal solutions. Exploring the limits of this constraint-identifying scenarios where a carefully crafted, potentially non-polynomial, algorithm could yield significant gains-presents a compelling avenue for research. Moreover, the focus remains largely on the algorithmic aspects. A complete understanding necessitates examining the physical realization of these codes – how the multiplicity matrix translates into actual read patterns, and how those patterns interact with the underlying storage medium.

Ultimately, the pursuit of reliable data storage is a study in trade-offs. This work highlights that every new dependency is the hidden cost of freedom. Future investigations should not only refine the algorithms, but also attempt to model the complete system – the interplay between code structure, channel noise, and the physical constraints of implementation – to truly understand the boundaries of what is achievable.

Original article: https://arxiv.org/pdf/2601.09947.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-01-16 19:20