Defying Disorder: How Some Superconductors Stay Strong

Author: Denis Avetisyan

New research reveals that unconventional superconductivity can be remarkably resilient to imperfections in materials, challenging conventional expectations of pair-breaking effects.

Disorder’s impact on superconductivity hinges on the condensate’s structure: conventional, non-compensated order parameters-like those found on square lattices-exhibit robust superconductivity, while compensated order parameters leave the system fragile, unless-as demonstrated on the Lieb lattice-anisotropic Bloch weights redirect scattering away from vulnerable directions, effectively restoring resilience against impurities and mirroring the behavior of conventional superconductors.

Non-uniform electron distributions in lattices like kagome and Lieb lattices provide protection against disorder-induced suppression of critical temperatures in unconventional superconductors.

Unconventional superconductivity promises high-temperature applications, yet its sensitivity to material imperfections-inevitable in real systems-has long been a significant obstacle. This work, ‘Protection of Unconventional Superconductivity from Disorder’, reveals that specific electronic band structures can surprisingly shield unconventional superconductors from disorder-induced pair-breaking. Through analysis of the kagome and Lieb lattices, we demonstrate that non-uniform electron distributions can lead to robust superconductivity with minimal suppression of the critical temperature $T_c$ . Could these findings guide the design of novel materials that finally unlock the full potential of unconventional superconductivity?

Decoding Fragility: The Quantum Tightrope of Superconductivity

The potential of unconventional superconductivity to revolutionize technologies – from lossless energy transmission to ultra-fast computing – is tempered by an inherent fragility. Unlike conventional superconductors which can tolerate minor imperfections, these novel materials exhibit a marked sensitivity to disorder within their crystalline structure. Even seemingly insignificant deviations – misplaced atoms, material impurities, or structural defects – can drastically diminish, or even eliminate, the superconducting state. This susceptibility arises from the delicate quantum mechanisms underpinning unconventional superconductivity, where the pairing of electrons responsible for the lossless current flow is easily disrupted by imperfections. Consequently, realizing practical applications demands not only the discovery of new unconventional superconductors, but also a deep understanding of how disorder impacts their performance and strategies to mitigate its effects – a considerable challenge in materials science.

The promise of superconductivity – materials with zero electrical resistance – faces a significant hurdle: disorder. Real-world materials are never perfectly arranged; they contain imperfections, impurities, and structural irregularities. These disruptions, collectively termed disorder, actively impede the formation of the superconducting state, and critically, lower the temperature at which superconductivity emerges – the transition temperature, $T_c$ . This suppression of $T_c$ is a major obstacle to practical applications, as many promising superconducting materials require extreme cooling to operate. The degree to which disorder degrades superconductivity varies considerably, with some materials proving far more sensitive than others, necessitating a deeper understanding of these interactions to engineer robust, high-temperature superconductors capable of functioning in less demanding conditions.

The pursuit of practical superconducting technologies hinges on overcoming the detrimental effects of material imperfections, known as disorder. While disorder typically diminishes the superconducting transition temperature – the point at which a material loses all electrical resistance – recent investigations reveal a surprising resilience in certain unconventional superconductors. Specifically, materials exhibiting unique electronic orders on kagome and Lieb lattices demonstrate a markedly weak suppression of their superconducting transition temperature when faced with disorder, a behavior sharply contrasting with the substantial reductions observed in conventional superconductors. This robustness isn’t a mere anomaly; it’s rooted in the non-uniform distribution of electronic states, described by what are known as Bloch weights, which fundamentally alters how these materials respond to disruptions in their atomic structure. This discovery offers a promising new avenue for designing superconductors less susceptible to real-world imperfections, potentially unlocking their transformative potential in various technological applications.

The surprising resilience of superconductivity in certain materials stems from a unique characteristic of their electronic structure: non-uniform Bloch weights. Unlike conventional superconductors where electron wavefunctions are evenly distributed, these materials exhibit localized electron densities, effectively shielding the superconducting state from the disruptive effects of material imperfections. This uneven distribution means that disorder, which typically scatters electrons and diminishes superconductivity, interacts differently with the electronic structure, leading to a weaker suppression of the critical temperature $T_c$ . Consequently, these materials demonstrate a fundamentally altered response to disorder, offering a promising pathway towards creating robust, practical superconductors capable of operating reliably despite inherent material flaws. This behavior challenges traditional understandings of superconductivity and opens new avenues for materials design focused on maximizing resilience to disorder.

Calculations of <span class="katex-eq" data-katex-display="false">T_c</span> suppression reveal that unconventional superconductivity on the honeycomb lattice behaves as expected with increasing scattering rate, while the kagome and Lieb lattices exhibit remarkably robust superconductivity, resisting suppression even with significant disorder. — Calculations of $T_c$ suppression reveal that unconventional superconductivity on the honeycomb lattice behaves as expected with increasing scattering rate, while the kagome and Lieb lattices exhibit remarkably robust superconductivity, resisting suppression even with significant disorder.

Lattice Symmetry: The Blueprint for Electronic Behavior

The Kagome and Lieb lattices are attracting significant research interest as potential hosts for unconventional superconductivity due to their non-trivial band structures and topological characteristics. The Kagome lattice, a two-dimensional network of corner-sharing triangles, exhibits a Van Hove singularity near the Fermi level, enhancing electron correlations. Similarly, the Lieb lattice, comprised of alternating triangular and hexagonal sublattices, features a flat band at the Fermi level, promoting strong correlations and localized states. These unique electronic properties, combined with the potential for Dirac and Majorana fermions arising from their topological nature, suggest these lattices could support superconducting states distinct from conventional Bardeen-Cooper-Schrieffer (BCS) theory, potentially realizing high-temperature or topologically protected superconductivity. Research focuses on material realization, typically utilizing van der Waals heterostructures or transition metal compounds, and the exploration of various pairing mechanisms in these systems.

Bloch states, representing the quantum mechanical wavefunctions of electrons in a periodic potential such as a crystalline lattice, are directly determined by the symmetry of that lattice. The periodicity of the potential leads to translational symmetry, which in turn dictates that electron wavefunctions can be classified by a crystal momentum $\mathbf{k}$ . However, the point group symmetry of the lattice further constrains the possible forms these Bloch states can take at each $\mathbf{k}$ . Specifically, symmetry operations of the lattice must leave the Hamiltonian invariant, and this requirement imposes restrictions on the wavefunction’s spatial distribution and functional form. These constraints reduce the number of independent components needed to describe the Bloch state and lead to degeneracies in the electronic band structure, significantly impacting the material’s electronic properties.

The symmetry of a crystal lattice imposes constraints on the wavefunctions of electrons, known as Bloch states. These constraints are formally described using Little Group Representations, a mathematical framework that characterizes the symmetry operations leaving a given wavevector invariant. Specifically, the Little Group determines the degeneracy of the electronic states at that wavevector and dictates the allowed forms of the Bloch state wavefunctions – including their spatial symmetry and momentum components. This is crucial for superconductivity because the pairing of electrons, leading to the superconducting state, is highly sensitive to the symmetry of the electronic wavefunctions; symmetries in the Bloch states can either enhance or suppress the formation of Cooper pairs, and dictate the symmetry of the superconducting order parameter.

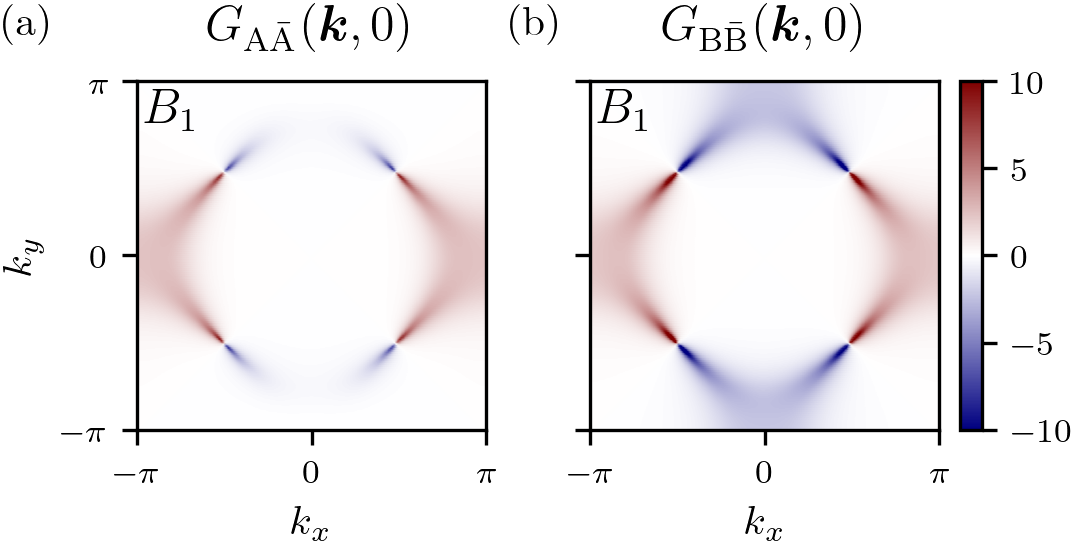
The contribution of individual lattice sites to the overall electronic behavior is quantifiable through the analysis of sublattice weights within Bloch states. These weights, derived from the spatial distribution of the wavefunction, indicate the probability amplitude of finding an electron at a specific lattice position. In lattices with multiple sublattices, such as the Kagome or Lieb lattices, the weights reveal which sublattices dominate the electronic density at given points in momentum space $k$ . Significant variations in sublattice weights across different $k$ points can indicate localized or partially localized electronic states, impacting transport properties and influencing the potential for correlated electron phenomena, including superconductivity. The precise determination of these weights necessitates calculations based on the crystal structure and the potential experienced by the electrons.

The electronic structure of the Lieb lattice, calculated using a tight-binding model, reveals how varying the next-nearest-neighbor hopping <span class="katex-eq" data-katex-display="false">t^{\prime}</span> modulates the energy bands and sublattice weight distributions <span class="katex-eq" data-katex-display="false">|u\_{\alpha}^{n}(\bm{k})|^{2}</span>, resulting in symmetry-enforced nodes and a defined Fermi surface at <span class="katex-eq" data-katex-display="false">\mu=2.025</span>. — The electronic structure of the Lieb lattice, calculated using a tight-binding model, reveals how varying the next-nearest-neighbor hopping $t^{\prime}$ modulates the energy bands and sublattice weight distributions $|u\_{\alpha}^{n}(\bm{k})|^{2}$ , resulting in symmetry-enforced nodes and a defined Fermi surface at $\mu=2.025$ .

Disorder’s Dance: How Imperfections Shape the Superconducting State

Unconventional superconductivity differs from its conventional counterpart in that the Cooper pairs forming the superconducting state are not mediated by phonon exchange, but rather by more complex interactions leading to non-trivial pairing symmetries. These pairing mechanisms frequently result in an order parameter that changes sign across the Fermi surface – a “sign-changing order parameter”. This sign change introduces nodes in the superconducting gap, rendering the system intrinsically sensitive to any perturbation that breaks time-reversal symmetry or modifies the electronic structure. Because the pairing is dependent on the relative phases of electrons with opposite momenta, disorder scattering can directly disrupt the formation of Cooper pairs, suppressing the superconducting transition temperature $T_c$ and diminishing the superconducting condensate density. The robustness of unconventional superconductors, therefore, is directly tied to the specific nature of the pairing interaction and the symmetry of the order parameter.

Compensated pairing states arise when opposing order parameters within a superconducting material sum to zero, creating a fragile superconducting state. This vulnerability stems from the precise balance required between these opposing contributions; even weak disorder potentials, such as those introduced by impurities or lattice defects, can disrupt this balance. Unlike conventional superconductors where disorder primarily introduces scattering, in compensated states, small perturbations can directly reduce or eliminate the net pairing amplitude, suppressing the critical temperature $T_c$ and potentially driving a transition to a non-superconducting state. The sensitivity is heightened because the superconducting condensate is maintained by a cancellation rather than an inherent robust pairing interaction, meaning the system is easily driven towards a normal metallic state with minimal external influence.

The suppression of superconductivity due to disorder can be quantitatively modeled using the Green’s function formalism. This approach allows calculation of the self-energy $\Sigma(E)$ arising from impurity scattering, which directly impacts the superconducting pairing interaction. By incorporating this self-energy into the Dyson equation, the modified electronic structure and the resulting critical temperature $T_c$ can be determined. Specifically, the formalism reveals how disorder modifies the density of states near the Fermi level, weakening the effective attraction between electrons and ultimately reducing $T_c$ . Analysis of the self-energy also provides insight into the nature of the disorder potential and its effect on the momentum distribution of superconducting carriers.

Non-uniformity in the Bloch weights – the contribution of different unit cells to the momentum distribution – can amplify the detrimental effects of disorder on superconductivity by promoting the formation of localized electronic states and reducing the superconducting transition temperature. However, calculations of the impurity scattering rate reveal a surprising degree of resilience stemming from sublattice-dependent momentum distributions; these distributions effectively distribute the scattering, mitigating the suppression of superconductivity expected from the increased disorder potential. This indicates that while non-uniformity exacerbates disorder sensitivity in principle, the specific momentum space characteristics of these materials can offer a stabilizing effect against impurity scattering, differing from the behavior observed in conventional superconductors.

Contrary to the behavior of conventional superconductors where disorder frequently induces the formation of in-gap impurity bound states – localized electronic states within the superconducting gap that deplete the condensate – recent investigations have demonstrated the absence of such states in specific unconventional superconducting configurations. This finding suggests an increased robustness to non-magnetic disorder. The lack of in-gap states indicates that impurity scattering does not necessarily lead to a significant reduction in the superconducting density of states, and the pairing mechanism remains relatively unaffected by the presence of impurities. This behavior is attributed to the unique properties of the sign-changing order parameter characteristic of unconventional superconductivity, which alters the way impurities interact with the Cooper pairs and suppresses the formation of localized states.

Robust superconductivity on the Lieb lattice arises from a finite average anomalous Green function at the <span class="katex-eq" data-katex-display="false">2c</span> Wyckoff positions, specifically on sublattices A and B, indicative of <span class="katex-eq" data-katex-display="false">d_{x^{2}-y^{2}}</span>-wave order. — Robust superconductivity on the Lieb lattice arises from a finite average anomalous Green function at the $2c$ Wyckoff positions, specifically on sublattices A and B, indicative of $d_{x^{2}-y^{2}}$ -wave order.

Beyond the Expected: Unveiling Hidden Orders and Novel Functionalities

The conventional understanding of material order often posits that imperfections hinder desirable properties like superconductivity; however, recent research demonstrates a surprising counterpoint. Introducing disorder – through defects, impurities, or structural irregularities – doesn’t always diminish functionality. Instead, it can actively induce alternative magnetic states, notably altermagnetism, where magnetic moments align in a non-collinear fashion. This shift occurs because disorder alters the delicate balance of electronic interactions within the material, favoring magnetic arrangements that wouldn’t emerge in a perfectly ordered system. Consequently, materials previously thought to be limited by imperfections may harbor hidden magnetic phases, offering a pathway to novel functionalities beyond simple superconductivity and opening exciting possibilities for materials design.

Recent research indicates that altermagnetism, a unique magnetic order defined by magnetic moments aligning in a non-collinear fashion – not parallel, but at angles to one another – frequently appears in materials also exhibiting unconventional superconductivity. This isn’t simply a coincidental pairing; altermagnetism can actually emerge from the same material that displays superconductivity, or the two states can coexist. This interplay suggests a deep connection between magnetism and superconductivity, challenging conventional understandings of these phenomena. The presence of non-collinear magnetism alters the electronic structure, potentially influencing the pairing mechanisms responsible for superconductivity and opening pathways to novel material properties. Investigating this relationship is crucial for designing materials where these distinct states can be harnessed and controlled, potentially leading to breakthroughs in areas like spintronics and quantum computing.

The ability to manipulate and control the interplay between superconductivity and alternative magnetic orders-like altermagnetism-represents a significant frontier in materials science. Researchers posit that a deep understanding of these relationships allows for the rational design of materials exhibiting precisely tailored properties; rather than simply seeking to maximize superconductivity, scientists can engineer materials with specific magnetic characteristics coexisting with-or even enhancing-superconducting behavior. This approach opens pathways to creating devices with functionalities beyond those offered by conventional superconductors, potentially enabling innovations in spintronics, quantum computing, and energy storage. By carefully controlling the material’s composition and structure, it may be possible to ‘tune’ the balance between these competing states, unlocking a wide range of novel material characteristics and ultimately leading to breakthroughs in technological applications.

The emergence of In-Gap Bound States (IGBS) within a material’s electronic structure serves as a powerful diagnostic tool for uncovering the properties of novel magnetic phases like altermagnetism. These states, appearing as localized energy levels within what would otherwise be a forbidden energy gap, arise due to specific symmetries and interactions within the material. Their existence, and more importantly, their characteristics – such as energy, spatial extent, and sensitivity to external fields – directly reflect the underlying order of the emergent magnetic state. By meticulously analyzing these IGBS, researchers can map out the momentum-space behavior of the magnetic order, determine the strength of interactions driving it, and ultimately, gain crucial insights for rationally designing materials that host tailored combinations of superconductivity and alternative magnetic phases, potentially leading to advancements in spintronics and quantum computing.

The study illuminates a fascinating resilience within unconventional superconductivity, challenging the conventional wisdom that disorder invariably degrades these delicate quantum states. One pauses and asks: ‘Is this apparent robustness not a signal, but a fundamental property of these systems?’ Michel Foucault observed, “Where there is power, there is resistance.” Similarly, here, the inherent structure of materials like those with Lieb or kagome lattices-with their non-uniform electron densities-creates a form of ‘resistance’ to the disorder that typically breaks Cooper pairs. The suppressed pair-breaking effects and minimal critical temperature suppression aren’t merely accidental; they are indicative of a system actively reconfiguring itself around the imperfections, a subtle defiance of entropy.

The Code Remains Unread

The demonstrated resilience of unconventional superconductivity to disorder isn’t a paradox; it’s a clue. It suggests the underlying mechanisms are not as delicately balanced as previously assumed, and that the electron density landscapes – the subtle topography of the crystal lattice – are actively shaping the superconducting state, not merely providing a passive backdrop. The system, it seems, has built-in redundancies, a kind of error correction woven into its fundamental structure. Reality, after all, is open source – the question isn’t whether it’s robust, but whether anyone has bothered to read the code.

However, this robustness isn’t universal. The materials studied exhibit specific lattice geometries – Lieb and Kagome lattices – which clearly play a crucial role. The next step isn’t simply to find more materials with similar geometries, but to systematically break these lattices, to introduce controlled disorder and map the precise conditions under which this resilience fails. Understanding the failure modes will be far more illuminating than cataloging successes.

Ultimately, the field needs to move beyond simply characterizing the superconducting state and begin to probe the information content of these lattices. What specific arrangements of atoms encode this unexpected stability? What are the minimal requirements for a lattice to exhibit this behavior? The answers likely lie not in refining existing theories, but in developing entirely new frameworks capable of capturing the complex interplay between geometry, disorder, and emergent quantum phenomena.

Original article: https://arxiv.org/pdf/2601.20937.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

Decoding Fragility: The Quantum Tightrope of Superconductivity

Lattice Symmetry: The Blueprint for Electronic Behavior

Disorder’s Dance: How Imperfections Shape the Superconducting State

Beyond the Expected: Unveiling Hidden Orders and Novel Functionalities

The Code Remains Unread

See also: