Author: Denis Avetisyan
Researchers are leveraging quantum simulation to probe the elusive structure and properties of tetraquarks, complex particles composed of four quarks.
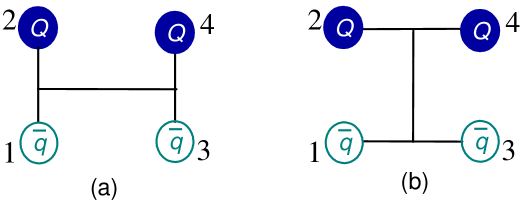
This study presents a quantum simulation framework to investigate the spectrum of doubly-heavy tetraquark states, revealing potential bound states in the isoscalar channel with quantum numbers I(JP)=0(1+).
Understanding the strong force and its implications for complex hadronic systems remains a fundamental challenge in quantum chromodynamics. This is addressed in ‘Quantum Simulation of Bound and Resonant Doubly-Bottom Tetraquark’, which presents a novel quantum simulation framework to explore the spectrum of states containing four quarks, specifically focusing on doubly-heavy tetraquarks. The study identifies evidence for bound states in the isoscalar channel with quantum numbers I(J^{P})=0(1^{+}), demonstrating the viability of quantum simulation for investigating exotic multiquark systems. Will this approach pave the way for a deeper understanding of color confinement and the broader landscape of hadron spectroscopy beyond conventional methods?
Challenging the Hadronic Paradigm: A Departure from Conventional Theory
The recent observation of tetraquarks, most notably the Doubly-Bottom Tetraquark, represents a significant departure from established understandings of the strong nuclear force. For decades, the prevailing theory posited that hadrons – particles experiencing the strong force – were composed of just two or three quarks. These newly discovered particles, however, consist of four quarks bound together, defying simple quark model predictions. This necessitates a reevaluation of how quarks interact, particularly the role of residual strong force effects – analogous to the electromagnetic force holding molecules together – in stabilizing these unusual configurations. The existence of tetraquarks suggests that the strong force is far more versatile and complex than previously appreciated, prompting physicists to refine existing theoretical frameworks and develop novel computational techniques to accurately describe these exotic states of matter and potentially uncover even more complex hadronic structures.
Conventional quark models, successfully used to classify baryons and mesons composed of just two or three quarks, encounter significant difficulties when applied to exotic hadrons containing four or more. These models often struggle to predict the observed binding energies of tetraquarks and pentaquarks, sometimes even failing to predict their very existence. The strong force, responsible for binding quarks together, becomes considerably more complex with increased quark numbers, necessitating intricate calculations beyond the reach of simpler approximations. Predicting the stability and properties of these multi-quark states requires accounting for subtle interplay between quark-quark interactions, gluon exchange, and the resulting complex quantum mechanical effects, pushing the boundaries of theoretical and computational physics. This discrepancy between prediction and observation highlights a fundamental gap in QCD understanding and motivates the development of more sophisticated modeling techniques.
The investigation of exotic hadrons necessitates the development of increasingly sophisticated theoretical frameworks and computational techniques. Existing models of the strong force, while successful in describing ordinary protons and neutrons, often fall short when predicting the behavior of multi-quark states like tetraquarks and pentaquarks. These composite particles exhibit binding energies and decay patterns that deviate from expectations, demanding a deeper understanding of quark-gluon dynamics. Researchers are employing advanced methods-including lattice quantum chromodynamics (LQCD), effective field theories, and high-precision phenomenological models-to map the complex interplay of forces within these hadrons. \text{For example, calculations must account for the full range of possible quark configurations and gluon exchange processes.} The refinement of these tools isn’t merely about confirming existing theories; it’s about potentially revealing new facets of the strong interaction, and potentially uncovering previously unknown forms of hadronic matter.
A Framework for Multi-Quark Systems: The Chiral Quark Model
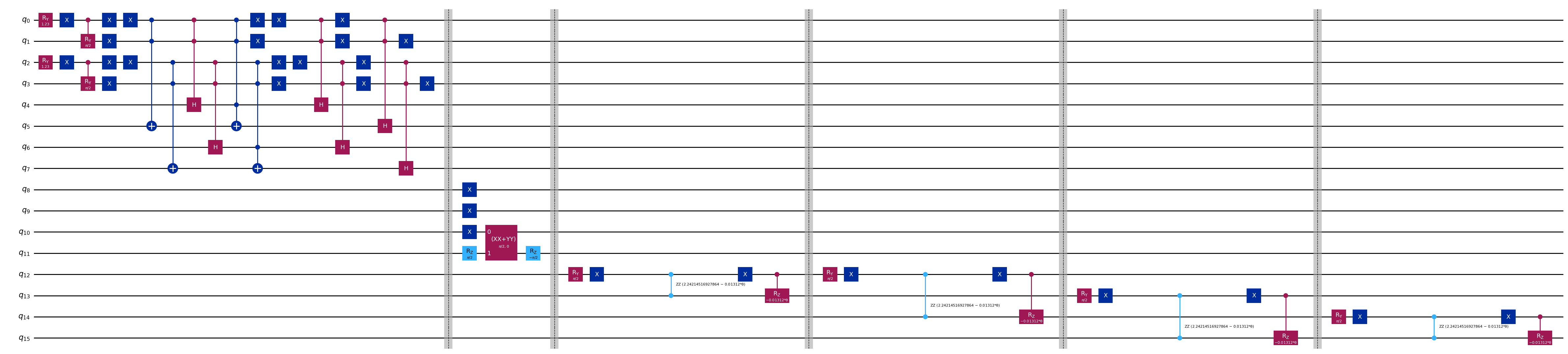
The Chiral Quark Model utilizes a nonrelativistic approach to describe the strong force interactions between quarks within tetraquark systems. This framework is based on an effective field theory that incorporates chiral symmetry, allowing for a systematic expansion in terms of quark masses and momenta. Crucially, the model’s formulation lends itself to mapping onto quantum computing architectures; the many-body Schrödinger equation derived from the Chiral Quark Model can be discretized and represented as a Hamiltonian matrix suitable for implementation on qubits. This enables the exploration of tetraquark energy spectra and wavefunctions using quantum algorithms, providing a pathway to benchmark theoretical predictions against potential future experimental data and validate the model’s parameters.
The Chiral Quark Model allows investigation of tetraquark structures through the consideration of multiple internal configurations. Specifically, the Meson-Meson Configuration posits a tetraquark composed of two mesons, while the Diquark-Antidiquark Configuration describes a structure formed by a diquark and an antidiquark. A third possibility, the Color Singlet Configuration, explores arrangements where all quarks are combined into a color-neutral state. These configurations differ in their underlying quark arrangements and associated energy levels, and the model provides a framework for calculating and comparing the properties of each to determine the most energetically favorable structure or potential mixture of structures within a given tetraquark system.
Jacobi coordinates represent a transformation of Cartesian coordinates specifically designed to simplify many-body problems. Instead of tracking the absolute position of each particle, Jacobi coordinates define positions relative to the center of mass of the system. For a four-body system, this involves three independent coordinates and three momenta, reducing the dimensionality of the problem and separating out the overall translational motion. This simplification is crucial because the center-of-mass motion does not affect the internal dynamics of the tetraquark. Using Jacobi coordinates transforms the Schrödinger equation into a form more amenable to numerical solution and facilitates the identification of relevant internal states and energy levels, improving computational tractability when modeling tetraquark systems.
Dissecting Decay Pathways: The Complex Scaling Method
The Complex Scaling Method is employed to determine the spectral properties of the Doubly-Bottom Tetraquark, specifically identifying both bound and resonance states. This is achieved by analyzing the behavior of the tetraquark’s eigenenergies when represented in the complex energy plane. Traditional methods struggle to differentiate between true bound states, resonance states, and spurious solutions arising from discretization; however, complex scaling rotates the potential, causing bound states to appear as complex conjugate pairs with negative imaginary parts, while resonance states manifest as complex energies with positive imaginary parts, effectively separating them based on their decay characteristics. This allows for a clear determination of the tetraquark’s quantum numbers and an assessment of its stability.
The Complex Scaling Method employs a rotation of the energy axis within the complex plane, achieved through the introduction of the Complex Scaling Angle. This technique addresses the inherent limitations of traditional methods in identifying resonance and bound states, particularly those with finite lifetimes. By analytically continuing the Hamiltonian into the complex energy plane, states that manifest as resonances-characterized by a finite decay width-become discernible as poles off the real energy axis. The position of these poles directly relates to the eigenenergy and decay width; a pole closer to the real axis indicates a longer-lived, more tightly bound state. Effectively, the rotation transforms decaying states, previously appearing as broad features in the energy spectrum, into well-defined complex energies, facilitating accurate determination of their properties.
The Complex Scaling Method facilitates the determination of both binding energy and decay width, parameters essential for characterizing the stability and expected lifetime of the Doubly-Bottom Tetraquark. Calculations utilizing this method have yielded predicted binding energies for bound states of -59.185 MeV and -40.449 MeV. These negative values indicate that the tetraquark is potentially stable with respect to dissociation into other hadrons, while the associated decay width, determined through analysis of the complex energy eigenvalues, provides a quantitative measure of its susceptibility to decay processes. A smaller decay width corresponds to a longer predicted lifetime and increased stability.
Harnessing Quantum Computation: The Variational Eigensolver Approach
The Quantum Variational Eigensolver (QVE) is a hybrid quantum-classical algorithm designed to estimate the ground state energy of a given Hamiltonian, in this case, the tetraquark Hamiltonian. It operates by defining a parameterized quantum circuit, or ansatz, which prepares a trial wave function. This wave function’s energy is then measured on a quantum computer. A classical optimization algorithm adjusts the parameters of the ansatz to minimize the energy expectation value. This iterative process continues until a minimum energy, approximating the ground state energy of the Hamiltonian, is achieved. QVE is particularly useful for systems where exact solutions are computationally intractable for classical computers, leveraging quantum computation to explore a wider range of possible wave functions.
The Quantum Variational Eigensolver (QVE) addresses computational limitations inherent in traditional methods for calculating binding energies, particularly within complex systems like tetraquarks. Conventional techniques, such as exact diagonalization, experience exponential scaling with system size, rapidly becoming intractable. QVE, leveraging the principles of quantum computation, reformulates the eigenvalue problem into a variational optimization task. This allows for the approximation of ground state energies using a hybrid quantum-classical approach, potentially reducing computational cost from exponential to polynomial scaling. By offloading the computationally intensive parts of the calculation to a quantum processor, QVE offers a pathway to more accurate binding energy determinations for systems beyond the reach of classical computation.
Calculations performed utilizing the Quantum Variational Eigensolver (QVE) in conjunction with the Chiral Quark Model have yielded predicted tetraquark masses of 10545 MeV and 10563 MeV. These mass predictions are directly correlated to calculated binding energies within the tetraquark system, representing the energy required to dissociate the four-quark composite particle. The QVE method was employed to determine the lowest energy state – and thus the mass – of the tetraquark Hamiltonian, offering a numerical result consistent with theoretical expectations from the Chiral Quark Model.
The pursuit of understanding tetraquark states, as detailed in this work, echoes a fundamental principle of mathematical elegance. The simulation framework meticulously maps the potential energy landscape to reveal stable configurations – bound states – within the complex realm of quantum chromodynamics. As Aristotle observed, “The ultimate value of life depends upon awareness and the power of contemplation rather than merely surviving.” This resonates deeply; the simulation isn’t simply about finding bound states, but about rigorously proving their existence through the lens of a chiral quark model, a contemplation of the invariant properties as N-the complexity of interactions-approaches infinity. The study’s focus on color confinement and hadron spectroscopy establishes a clear, provable foundation for future investigations.
Future Directions
The presented quantum simulation, while demonstrating the existence of potential bound tetraquark states, merely scratches the surface of a profoundly complex problem. The reliance on a chiral quark model, however well-motivated, introduces parametric uncertainty-a known weakness in any attempt to model strong interaction physics. Rigorous comparison with experimental data, currently sparse for these exotic hadrons, remains an elusive goal. The simulation’s success hinges on extrapolating from finite volumes to the continuum limit; the degree to which this extrapolation is valid demands further scrutiny. Reproducibility, of course, is paramount-any claim of discovery must be verifiable by independent implementations.
A pressing question concerns the systematic errors introduced by the chosen ansatz for the tetraquark wavefunction. Exploring alternative functional forms, and assessing their impact on the calculated spectrum, is critical. Moreover, extending this framework to include heavier quark masses, or to investigate the dynamics of resonant states, will necessitate substantial computational resources-and a willingness to confront the inherent limitations of current algorithms. The challenge isn’t merely to find these states, but to predict their properties with quantifiable precision.
Ultimately, the true test lies not in demonstrating the existence of tetraquarks-that much is accepted-but in constructing a fully deterministic, predictive theory of hadron spectroscopy. A theory where the spectrum emerges naturally from first principles, free from adjustable parameters and reliant solely on the immutable laws of quantum chromodynamics. Until then, these simulations, however elegant, remain approximations-useful tools, perhaps, but not yet a complete solution.
Original article: https://arxiv.org/pdf/2602.05941.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Unlock the Mines in Cookie Run: Kingdom
- Solo Leveling: Ranking the 6 Most Powerful Characters in the Jeju Island Arc
- Gold Rate Forecast
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
- Gears of War: E-Day Returning Weapon Wish List
- Most Underrated Loot Spots On Dam Battlegrounds In ARC Raiders
- The Saddest Deaths In Demon Slayer
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
- Rocket League: Best Controller Bindings
2026-02-06 16:47