Author: Denis Avetisyan
New research reveals that unexpected multi-hadron states induced by calculation methods can significantly skew results in lattice QCD calculations of hadron properties.
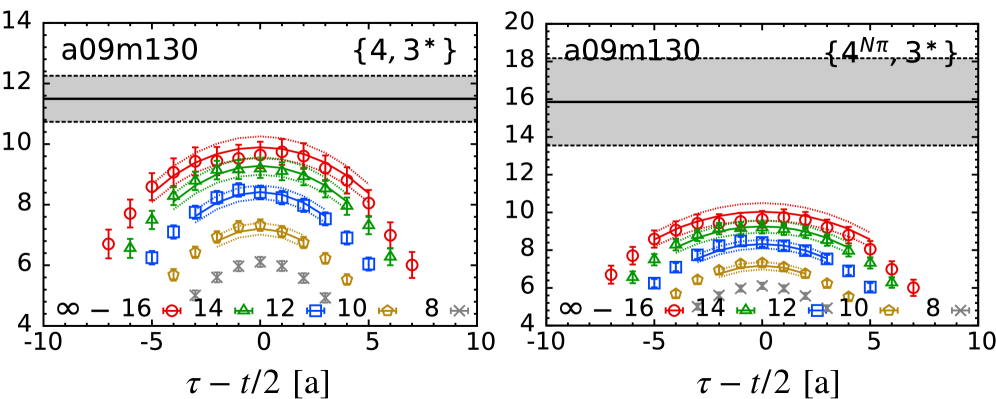
Current-enhanced excited states in lattice QCD three-point functions necessitate careful analysis to mitigate contamination and ensure accurate extraction of hadron matrix elements.
Precise determinations of hadron structure from lattice QCD are often hampered by systematic uncertainties arising from excited-state contamination. This work, titled ‘Evidence of current-enhanced excited states in lattice QCD three-point functions’, identifies a mechanism where the choice of inserted current and kinematics can selectively enhance specific excited states contributing to three-point functions. The analysis, supported by both numerical results and predictions from chiral perturbation theory, demonstrates that these current-enhanced states can significantly impact calculations of hadron matrix elements. Understanding and controlling these effects-potentially through variational methods or improved perturbative treatments-is crucial for extracting reliable insights into hadron structure from first-principles calculations.
Whispers of Complexity: The Challenge of Excited States
Lattice Quantum Chromodynamics (LQCD) presents a powerful, first-principles method for determining the properties of hadrons – composite particles like protons and neutrons – directly from the fundamental theory of strong interactions. However, achieving the desired precision in these calculations is a significant challenge due to a phenomenon known as excited-state contamination. The mathematical framework inherently includes contributions not only from the hadron’s ground state – its lowest energy configuration – but also from all higher energy, or ‘excited’, states. Isolating the ground-state signal is crucial, as these excited-state contributions can mimic or mask the true properties of the hadron being studied. Without effective methods to suppress or account for this contamination, theoretical predictions can diverge substantially from experimental results, limiting the ability of Lattice QCD to provide reliable insights into the strong force and the structure of matter.
The fundamental challenge of excited-state contamination stems from the inherent nature of quantum calculations; these do not exclusively isolate the ground state, but instead sum contributions from all possible energy levels of the system. Imagine attempting to discern a single, quiet note within a complex chord – the higher-energy “excited states” act as dissonant overtones, obscuring the clear signal originating from the lowest-energy, ground state. This poses a significant problem for Lattice QCD because physical properties, such as hadron masses, are determined by the ground state, and these higher-energy contributions introduce systematic errors. Effectively, the calculated result becomes a mixture of the desired ground-state property and unwanted noise from excited states, requiring sophisticated techniques to disentangle them and obtain a precise prediction that accurately reflects reality.
The predictive power of Lattice QCD calculations hinges on accurately isolating the ground state of hadrons, but uncontrolled excited-state contamination introduces systematic errors that can dramatically skew theoretical results. These errors aren’t merely statistical fluctuations; they represent a fundamental misunderstanding of the system being modeled, leading to discrepancies with experimental data. A particularly striking example lies in the Goldberger-Treiman relation, a cornerstone of chiral perturbation theory, where violations of up to 40% have been observed in Lattice QCD calculations – a consequence of neglecting contributions from excited states involving multiple pions Nπ. This substantial deviation underscores the critical need for advanced techniques to suppress excited-state effects and ensure the reliability of theoretical predictions, ultimately maximizing the potential of Lattice QCD as a precision tool for understanding the strong force.
Dissecting the Signal: Methods for Extracting Matrix Elements
In Lattice Quantum Chromodynamics (LQCD), three-point correlation functions are fundamental to the calculation of hadron matrix elements. These functions connect an initial hadronic state |i\rangle with a final hadronic state |f\rangle through the insertion of local current operators \mathcal{O}. Specifically, the three-point function takes the form \langle f | \mathcal{O} | i \rangle, representing the amplitude for the transition between these states induced by the operator. By analyzing the time dependence of this correlation function on a discretized spacetime lattice, and employing appropriate renormalization procedures, one can extract the desired matrix element, which characterizes the strong interaction properties of the hadrons. The precision of this extraction relies heavily on controlling statistical and systematic uncertainties inherent in the lattice calculation.
Three-point correlation functions, while fundamental to determining hadron matrix elements in Lattice QCD, are inherently vulnerable to Excited State Contamination (ESC). ESC arises from the contributions of higher energy states to the measured signal, distorting the extraction of the desired ground state matrix element. To mitigate ESC, techniques such as the Generalized Eigenvalue Problem (GEVP) and Variational Analysis are employed. GEVP constructs ratios of correlation functions to project out the ground state, effectively suppressing contributions from excited states. Variational Analysis, similarly, involves constructing a basis of operators and performing a simultaneous fit to multiple correlation functions, allowing for the explicit inclusion and subsequent subtraction of excited state contributions. Both methods aim to isolate the ground state signal, improving the accuracy and reliability of matrix element determinations.
Multi-state fitting, as applied to the extraction of hadron matrix elements from lattice QCD correlation functions, moves beyond isolating the ground state by directly incorporating contributions from excited states. Instead of attempting to suppress excited-state contamination, this method simultaneously fits the correlation functions with a sum of exponentials, each corresponding to a different energy level E_n . The fitting parameters include the matrix element of interest and the amplitudes associated with each state. By explicitly modeling the contributions from multiple energy levels, multi-state fits significantly reduce systematic uncertainties arising from excited-state effects, provided the fit is well-defined and sufficient excited states are included to adequately represent the spectrum. The accuracy of the extracted matrix element is directly tied to the correct identification of the excited state energies and amplitudes within the fitting procedure.
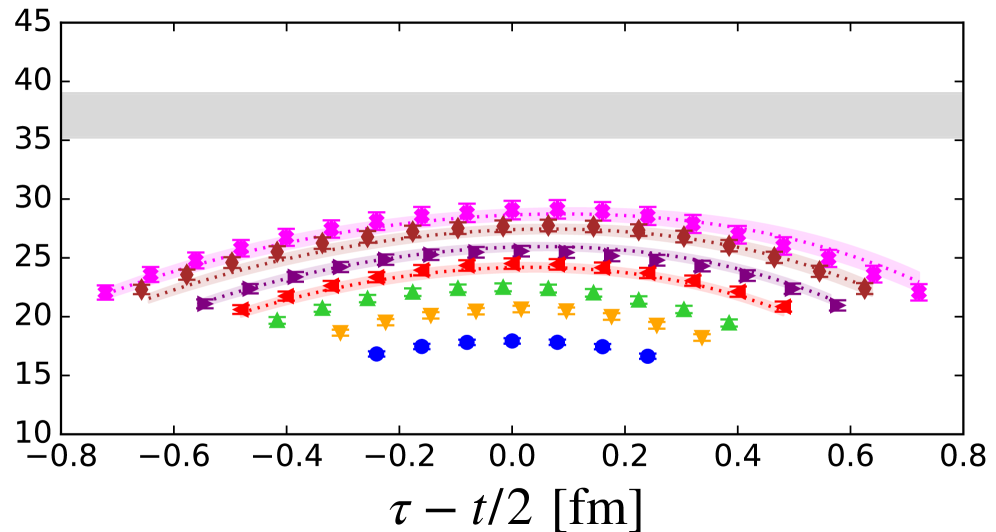
![GEVP analysis, performed using pseudoscalar and temporal axial-vector currents at non-zero momentum transfer, demonstrates consistent ratios across different source-sink separations for both the <span class="katex-eq" data-katex-display="false">m_{\pi} = 429~\rm MeV</span> results from Barca et al. [2023] and the <span class="katex-eq" data-katex-display="false">m_{\pi} = 346~\rm MeV</span> results from the ETM collaboration [2024].](https://arxiv.org/html/2602.17195v1/x7.png)
Tracing the Shadows: Identifying Key Contributory States
Chiral Perturbation Theory (ChPT) is an effective field theory utilized to describe the low-energy interactions of hadrons, particularly those involving pions and nucleons. It is based on the spontaneous breaking of chiral symmetry in Quantum Chromodynamics (QCD) and provides a systematic expansion in terms of p^2 , where p represents the momentum scale of the process. Within ChPT, excited-state contributions (ESCs) – arising from intermediate states with higher energies than the ground state – can be estimated and analyzed. By treating these excited states as virtual particles exchanged during interactions, ChPT allows for the calculation of their impact on observable quantities, offering a means to quantify the size of corrections to calculations performed only considering the ground state and providing a framework for understanding how these contributions affect the overall theoretical predictions.
Excited-state contributions (ESC) in lattice QCD calculations are significantly impacted by the presence of N\pi states, which represent nucleon-pion configurations contributing to the excited hadron spectrum. These multi-hadron states introduce complexities because their interactions and mixing with the ground state necessitate careful consideration during data analysis. The N\pi states are not simply single-particle excitations but rather represent intermediate states in the decay or scattering processes relevant to hadron structure, thereby influencing the observed energy levels and transition amplitudes. Accurate modeling and subtraction of these ESC arising from N\pi configurations is crucial for extracting precise values of hadron properties from lattice simulations.
Current enhancement describes a phenomenon in lattice QCD calculations where the specific mathematical form of the current operator-used to probe hadron properties-overlaps strongly with the wavefunctions of excited hadronic states. This amplified overlap increases the contribution of these excited states to observable quantities, even within finite volume simulations where such contributions are typically expected to be suppressed. The effect is not simply a matter of large excited-state contamination; it introduces an enhancement proportional to the volume, potentially leading to unexpectedly large and unsuppressed contributions from multi-hadron states. This necessitates careful consideration of current structure when interpreting lattice QCD results and can require specialized techniques to accurately isolate the ground state signal or quantify the excited-state contributions.
![The ratio of Wilson quark to domain-wall fermion contributions, calculated using the <span class="katex-eq" data-katex-display="false">N\pi</span> interpolator and varying source-sink separation <span class="katex-eq" data-katex-display="false">t_S</span>, differs between ensembles “cA24” (<span class="katex-eq" data-katex-display="false">L=2.27~\rm fm</span>, <span class="katex-eq" data-katex-display="false">m_\pi=346~\rm MeV</span>) and “cA48” (<span class="katex-eq" data-katex-display="false">L=4.50~\rm fm</span>, <span class="katex-eq" data-katex-display="false">m_\pi=131~\rm MeV</span>), as detailed in Alexandrou et al. [2024].](https://arxiv.org/html/2602.17195v1/x9.png)
The Echoes of Precision: Matrix Element Dependence and Validation
The isoscalar scalar matrix element – a fundamental quantity characterizing how hadrons interact – exhibits a notable sensitivity to the presence of the σ meson. This arises because the σ meson, a relatively light scalar resonance, contributes significantly to the overall scattering amplitude for interactions involving these hadrons. Consequently, precise determination of this matrix element serves as a crucial test of models attempting to describe the σ meson’s nature – is it a conventional quark-antiquark state, or something more exotic like a tetraquark or a glueball? Subtle variations in the measured value of the isoscalar scalar matrix element can thus provide valuable insights into the internal structure and decay mechanisms of the σ meson, and ultimately refine theoretical understanding of strong force dynamics.
The Goldberger-Treiman relation, a cornerstone of understanding strong interactions, reveals a deep connection between axial-vector and pseudoscalar currents within hadron physics. This relation doesn’t merely describe a correlation; it provides powerful constraints on the calculation of hadron matrix elements, which are fundamental quantities characterizing how hadrons interact. By linking the axial-vector current – responsible for beta decay – to the pseudoscalar current associated with pion emission, the relation effectively reduces the number of independent matrix elements needing direct calculation. This simplification is crucial, as direct computation of these elements from first principles is notoriously difficult. Consequently, the Goldberger-Treiman relation acts as a vital theoretical check, ensuring the consistency of calculated hadron properties and enabling more reliable predictions in the complex realm of quantum chromodynamics. g_{A}/g_{V} = F(q^2)/f_{\pi} represents this relationship, where g_{A} and g_{V} are the axial and vector coupling constants, and f_{\pi} is the pion decay constant.
The precise calculation of hadron matrix elements represents a cornerstone in validating theoretical frameworks used to describe the strong force, and recent advancements have unlocked a new level of accuracy in these determinations. Historically, extracting these fundamental quantities has been hampered by contributions from excited hadronic states, which obscure the ground-state signal and introduce systematic uncertainties. This work demonstrates a robust methodology for systematically controlling this excited-state contamination, allowing for a cleaner extraction of matrix element values. Consequently, a more rigorous comparison between theoretical predictions-derived from models like chiral perturbation theory and lattice quantum chromodynamics-and experimental observations becomes possible, promising to refine our understanding of how quarks and gluons assemble into the visible matter of the universe and pushing the boundaries of strong interaction physics.
The pursuit of hadron matrix elements within lattice QCD reveals a landscape less of definitive answers and more of echoing uncertainties. This work illuminates how current-induced multi-hadron states amplify excited-state contamination, a phenomenon akin to whispers growing into a cacophony. It isn’t a failure of the calculation, but rather an acknowledgment of the inherent noise within the system. As Søren Kierkegaard observed, “Life can only be understood backwards; but it must be lived forwards.” Similarly, these calculations proceed despite the imperfect grasp on the underlying states, demanding tools like variational analysis to navigate the ambiguities and, ultimately, persuade the data toward a meaningful result. The precision sought isn’t an elimination of error, but a skillful dance with it.
Where Does the Signal Go?
The persistent issue of excited-state contamination isn’t merely a nuisance; it’s a confession. A confession that these calculations, for all their mathematical elegance, remain profoundly susceptible to the whispers of the uncalculated. This work reveals that current enhancement doesn’t simply add to the noise-it conjures states, multi-hadron phantoms that thrive in the gaps between approximations. The tidy separation of ground and excited states proves, once again, a convenient fiction. Every variational analysis feels less like a solution, and more like a carefully constructed containment field.
The reliance on chiral perturbation theory as a corrective feels particularly… hopeful. As if a few well-chosen parameters can tame the inherent chaos of strong interactions. It’s a pragmatic approach, certainly, but it doesn’t address the fundamental question: how much of the ‘signal’ is actually borrowed from the void? Future work must confront the possibility that these excited states aren’t simply errors to be subtracted, but integral components of the system, demanding a more holistic, less reductive, approach.
Perhaps the true path lies not in refining the current formalism, but in abandoning the expectation of a clean, isolated ground state. To accept that everything unnormalized is still alive, and that the ‘true’ result is always a superposition of possibilities. The data isn’t truth; it’s a truce between a bug and Excel, and the terms of that truce are always shifting.
Original article: https://arxiv.org/pdf/2602.17195.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Poppy Playtime Chapter 5: Engineering Workshop Locker Keypad Code Guide
- Jujutsu Kaisen Modulo Chapter 23 Preview: Yuji And Maru End Cursed Spirits
- God Of War: Sons Of Sparta – Interactive Map
- 8 One Piece Characters Who Deserved Better Endings
- Who Is the Information Broker in The Sims 4?
- Mewgenics Tink Guide (All Upgrades and Rewards)
- Pressure Hand Locker Code in Poppy Playtime: Chapter 5
- I Used Google Lens to Solve One of Dying Light: The Beast’s Puzzles, and It Worked
- Engineering Power Puzzle Solution in Poppy Playtime: Chapter 5
- Poppy Playtime Chapter 5: Emoji Keypad Code in Conditioning
2026-02-21 05:55