Author: Denis Avetisyan
New analysis of heavy-ion collisions is refining our understanding of the fundamental state of matter at extreme temperatures and densities.
Bayesian analysis of particle yields from Ru+Ru and Zr+Zr collisions provides precise constraints on the QCD phase diagram and chemical potential differentials.
Understanding the interplay of thermodynamic variables in quantum chromodynamics (QCD) remains a central challenge in nuclear physics. This is addressed in ‘Chemical potential differentials in the QCD phase diagram from heavy-ion isobar collisions’, which explores correlations between temperature and baryon, charge, and strangeness chemical potentials using data from Ru+Ru and Zr+Zr collisions. By employing Bayesian thermal analysis of hadron yields, the research demonstrates a precision mapping of the four-dimensional QCD phase diagram and constrains theoretical predictions from lattice-QCD and chiral mean field models. How will these refined thermodynamic constraints inform our understanding of the equation of state and critical phenomena in strongly interacting matter?
Mapping the Quantum Mess: A Pragmatic View
The quest to map the quantum chromodynamics (QCD) phase diagram hinges on a detailed understanding of particle creation in environments of immense energy density and temperature. At these extreme conditions – reminiscent of the very early universe or the cores of neutron stars – matter undergoes a phase transition from ordinary hadronic matter to a quark-gluon plasma. Precisely characterizing the types and abundances of particles produced during this transition is therefore paramount; these particles serve as vital probes of the plasmaâs properties. However, accurately predicting particle yields requires navigating a complex interplay of factors, including temperature, baryon chemical potential, and collision dynamics. Subtle variations in these conditions can dramatically alter the observed particle spectrum, demanding experimental data of exceptional precision and theoretical models capable of faithfully reproducing the conditions at play. Ultimately, unraveling the QCD phase landscape relies on transforming the âfingerprintâ of particle production into a precise readout of the underlying quantum state of matter.
Current theoretical models attempting to map the quantum chromodynamics (QCD) phase landscape face significant hurdles due to the intricate relationships between key thermodynamic variables – temperature, baryon chemical potential, and strangeness – and the pronounced effects of isospin. These factors don’t operate in isolation; instead, they exhibit complex, often non-linear interactions that challenge the simplifying assumptions of many conventional approaches. Specifically, the relative abundance of protons and neutrons – governed by isospin – demonstrably influences the transition between hadronic matter and the quark-gluon plasma, and its accurate representation is vital for precise predictions. Failing to fully account for these interconnected effects introduces substantial uncertainties when comparing theoretical calculations to the particle composition observed in heavy-ion collision experiments, hindering a complete understanding of the matter created at extreme energy densities.
The interpretation of experimental data from heavy-ion collisions hinges on a precise understanding of chemical freeze-out, the pivotal moment when particle production effectively stops and the created matter begins to evolve freely. This isn’t a sharp, instantaneous event, but rather a gradual process influenced by temperature, density, and the interplay of various particle species. Determining the conditions at which chemical freeze-out occurs allows physicists to extrapolate backwards and infer the properties of the matter created in these collisions – its temperature, baryon chemical potential, and overall composition. Sophisticated modeling techniques, often incorporating statistical and thermodynamic principles, are employed to connect the observed abundances of different particles – pions, kaons, protons, and so on – with the parameters characterizing this freeze-out surface. Any discrepancy between theoretical predictions and experimental measurements necessitates a refinement of these models, potentially revealing new insights into the fundamental nature of quantum chromodynamics and the strong force.
A comprehensive understanding of the quark-gluon plasma and the transitions within the QCD phase diagram hinges on a reliable connection between theoretical predictions and experimental observations of particle abundances. Establishing this link necessitates a robust theoretical framework capable of accurately simulating the complex dynamics of particle production and subsequent chemical freeze-out. This framework must account for the myriad of particle species created in high-energy collisions, their interactions, and the subtle influences of factors like baryon chemical potential and temperature. By precisely predicting particle yields – the number of each type of particle produced – researchers can rigorously test the validity of different theoretical models and refine \text{QCD} calculations. Ultimately, this iterative process of comparison between theory and experiment allows scientists to map the QCD phase landscape and gain insights into the fundamental properties of matter under extreme conditions.
Statistical Wrangling: A Pragmatic Approach
A Bayesian analysis is employed to determine the freeze-out parameters of the system using experimental datasets. This statistical approach allows for the incorporation of prior knowledge and the propagation of uncertainties throughout the analysis, yielding not only best-estimate values for parameters such as temperature \mu_B and baryon chemical potential, but also a full probability distribution representing the uncertainty in these values. The resulting posterior distributions provide robust uncertainty quantification, crucial for evaluating the reliability of extracted parameters and comparing results with theoretical predictions. This method differs from frequentist approaches by providing probabilities for parameter values themselves, rather than confidence intervals based on repeated sampling.
The computational demands of Lattice-QCD calculations preclude their direct use within a Bayesian analysis requiring numerous evaluations of the Equation of State. To address this, a Gaussian Process Emulator serves as a surrogate model, effectively approximating the Lattice-QCD results. This emulator is trained on a dataset of Lattice-QCD calculations performed at specific parameter points, allowing it to predict the Equation of State at new, unseen parameter values with quantified uncertainty. The emulatorâs predictive capability significantly reduces computational time, enabling efficient exploration of the parameter space during the Bayesian inference process, while maintaining accuracy consistent with the underlying Lattice-QCD data.
The Bayesian analysis utilizes the BQS (Bielefeld-Quark-Hadron) Equation of State, a thermodynamic model originating from first-principles Lattice-QCD calculations. This equation of state provides a relationship between pressure, temperature, and baryon chemical potential, accurately describing the state of matter created in heavy-ion collisions. The BQS equation of state is characterized by its parameterization of the quark-hadron transition and is crucial for translating experimental observables into constraints on the collision dynamics and freeze-out conditions. It allows for the precise calculation of thermodynamic quantities, such as energy density and entropy, necessary for interpreting the experimental data and extracting meaningful physical insights.
The Chiral Mean Field Model refines the BQS Equation of State by incorporating effects related to baryon stopping. This is achieved through the introduction of a parameter, α, which modulates the influence of these effects on the overall thermodynamic description of the system. Specifically, a value of α = 0.543 is utilized, representing the calibrated strength of the baryon stopping contribution within the model. This adjustment allows for a more accurate representation of the systemâs evolution and final state by accounting for the reduction in baryon velocities as they interact with the surrounding medium.
Isobar Collisions: Probing the System
Isobar collisions utilizing Ruthenium-96 (96Ru) and Zirconium-96 (96Zr) nuclei are employed to investigate the influence of isospin on chemical freeze-out conditions. These nuclei possess identical mass numbers but differing proton/neutron ratios, allowing for a systematic variation of isospin while minimizing effects from collision centrality or energy. By comparing particle production yields from 96Ru + 96Ru and 96Zr + 96Zr collisions at the same center-of-mass energy, researchers can isolate the contribution of isospin to the chemical potential and temperature parameters that characterize the transition from the quark-gluon plasma to hadronic matter. This technique provides a controlled method for probing the equation of state of strongly interacting matter and its dependence on baryon versus meson content.
The Blast-Wave model is employed to analyze particle spectra generated in Ruthenium-96 and Zirconium-96 collisions, enabling the extraction of particle yields and relevant thermodynamic parameters. This model assumes that particles originate from a common freeze-out surface, characterized by a local temperature and flow velocity. By fitting the observed particle spectra – specifically, the transverse momentum distributions and particle ratios – with the Blast-Wave function, we determine the parameters describing this freeze-out surface. The resulting particle yields, derived from the fitted Blast-Wave parameters, serve as essential input for a Bayesian analysis, allowing for a statistical assessment of the isospin dependence of the freeze-out conditions and the subsequent determination of the QCD phase diagram.
Analysis of particle yields from Ruthenium-96 and Zirconium-96 collisions reveals isospin-dependent effects on the chemical freeze-out process. These isobar collisions, differing only in neutron/proton ratio, demonstrate a measurable sensitivity in final state particle production. Quantitative comparison of the observed yields indicates an approximate 20 MeV difference in the Baryon Chemical Potential \Delta\mu_B between the two systems. This discrepancy provides a direct constraint on the isospin dependence of the equation of state at the conditions achieved in heavy-ion collisions and allows for refinement of theoretical models describing the QCD phase diagram.
Utilizing experimental data from Ruthenium-96 and Zirconium-96 isobar collisions, and subsequent analysis with a Blast-Wave function and Bayesian statistics, provides a means to test the validity of current theoretical models describing the strong interaction. Discrepancies or agreements between predicted and observed particle yields, particularly concerning the isospin dependence revealed by these collisions, allow for iterative refinement of parameters within these models. This process directly impacts the precision with which the QCD phase diagram – a map of quark-gluon plasma formation as a function of temperature and baryon density – can be constructed and understood, ultimately leading to a more accurate depiction of matter under extreme conditions.
Net-Charge and System Characteristics: A Pragmatic View
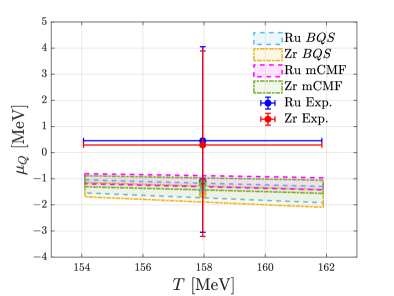
Precise determination of net-charge-the difference between positively and negatively charged particles-provides a crucial window into the properties of strongly interacting matter. Researchers utilize a technique called Double Ratios, which involves examining ratios of particle yields to minimize uncertainties stemming from volume fluctuations and overall normalization. This method allows for a more accurate assessment of charge neutrality within the system, revealing if equal amounts of positive and negative charge are present. The resulting measurements arenât merely a confirmation of expected behavior; they serve as a sensitive probe of the systemâs conditions, influencing the interpretation of other key parameters like temperature and baryon chemical potential, and ultimately providing insights into the fundamental nature of the quark-gluon plasma created in heavy-ion collisions.
A sophisticated Bayesian analysis, intricately linked with the THERMUS grand canonical ensemble code, allows for the determination of key parameters characterizing the state of strongly interacting matter created in heavy-ion collisions. This combined approach doesn’t simply provide single values for the chemical freeze-out temperature and baryon chemical potential; instead, it yields robust probability distributions, accounting for systematic uncertainties inherent in the experimental measurements and theoretical modeling. The resulting parameter space provides statistically sound estimates of the conditions under which hadrons cease to be created, offering critical constraints on the equation of state and the phase diagram of quantum chromodynamics.
Analysis of the experimental data has yielded a compelling result: the ratio of the baryon chemical potential difference to the electric charge chemical potential difference, expressed as \Delta\mu_B / \Delta\mu_Q, is remarkably close to -1. This finding isnât merely an observation; it provides significant validation for theoretical models attempting to describe the state of matter created in high-energy collisions. Specifically, the result aligns with predictions generated by both the Boltzmann Quantum Statistics (BQS) model and the modified Color-Glass Condensate (mCMF) framework, strengthening confidence in their ability to accurately capture the fundamental characteristics of strongly interacting matter. The consistency between experimental findings and these leading theoretical approaches represents a crucial step forward in understanding the complex interplay of charges and baryon number in extreme conditions.
The investigation into strongly interacting matter, a state of matter existing at extreme temperatures and densities, benefits from these refined measurements of net-charge and system characteristics. By establishing a clearer picture of charge neutrality and parameters like the chemical freeze-out temperature and baryon chemical potential, researchers gain access to previously obscured details of the quark-gluon plasma. The observed ratio of \Delta\mu_B/\Delta\mu_Q = -1 provides crucial validation for theoretical models – specifically both the Boltzmann-Gibbs statistics (BQS) and the multi-component modified Fermi gas (mCMF) – strengthening confidence in their ability to describe the behavior of this exotic state. This deeper understanding not only advances fundamental knowledge of quantum chromodynamics but also provides a more complete framework for interpreting experimental results from heavy-ion collision experiments, ultimately revealing the properties of matter under extreme conditions.
The pursuit of mapping the QCD phase diagram, as detailed in this research, feels predictablyâŠinvolved. All this Bayesian analysis of particle yields from isobar collisions – Ru+Ru and Zr+Zr, no less – simply refines the edges of what was already suspected. Itâs a rigorous attempt to quantify the correlations between chemical potentials, striving for precision where inherent messiness resides. One recalls Mary Wollstonecraftâs observation that âIt is time to revolve in our own minds the rights of man,â and it seems this work is doing just that – meticulously examining the ârightsâ of quarks and gluons. This isnât innovation, of course; itâs simply the old problem of extracting signal from noise, now with fancier statistical methods and more comprehensive datasets. Everything new is just the old thing with worse docs.
What Comes Next?
The pursuit of the QCD phase diagram resembles an endless refinement of boundary conditions. This work, leveraging the admittedly clean signal of isobar collisions, offers yet another, more detailed map – but maps are not territory. The insistence on strangeness neutrality, while computationally convenient, feels increasingly like a simplifying assumption rather than a fundamental truth. The bug tracker, in this case the discrepancy between Bayesian posterior distributions and increasingly ambitious theoretical models, is filling up. It is tempting to believe that exquisitely precise chemical freeze-out parameters will unlock the secrets of strongly coupled matter; however, the history of this field suggests that each resolved feature will simply reveal a new layer of complexity.
The real challenge isnât parameter estimation; itâs model building. Current equations of state, while improving, still appear to be fitting functions dressed up as theory. The next generation of analysis will likely require incorporating data from smaller collision systems, where the initial conditions are less idealized – and the resulting chaos more representative of what actually happens. Attempts to constrain fluctuations beyond the simple thermodynamic limit will, predictably, encounter the limitations of finite statistics and the ever-present spectre of systematic uncertainties.
Ultimately, the effort isnât about finding the phase diagram. Itâs about building the tools to describe a system that resists simple categorization. The process doesnât yield answers; it generates better questions. The research doesn’t deploy – it lets go.
Original article: https://arxiv.org/pdf/2601.21232.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Gold Rate Forecast
- How to Unlock the Mines in Cookie Run: Kingdom
- Jujutsu: Zero Codes (December 2025)
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
- How To Upgrade Control Nexus & Unlock Growth Chamber In Arknights Endfield
- Top 8 UFC 5 Perks Every Fighter Should Use
- Most Underrated Loot Spots On Dam Battlegrounds In ARC Raiders
- Gears of War: E-Day Returning Weapon Wish List
- USD RUB PREDICTION
- Top Anime Like Iâm the Evil Lord of an Intergalactic Empire You Canât Miss
2026-01-31 17:51