Passive QKD: A Rigorous Security Analysis

by

Author: Denis Avetisyan

A new proof demonstrates the security of a practical quantum key distribution system using a simplified, passive measurement approach.

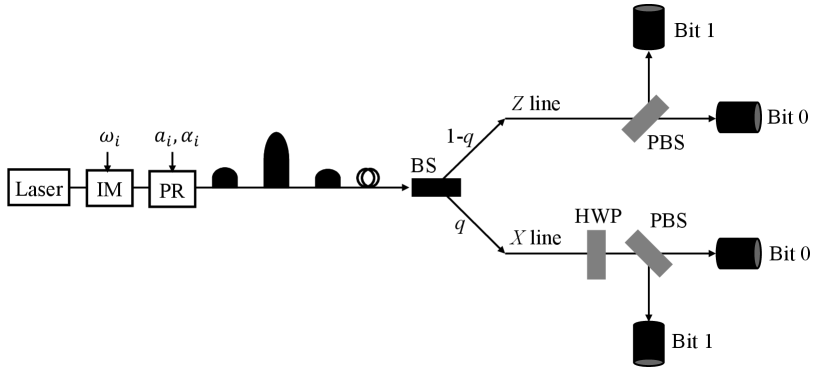
A passive decoy-state BB84 protocol utilizes phase-randomized coherent states-characterized by intensity $\mu_{\omega_i}$ and polarization $\phi(a_i, \alpha_i)$-to transmit quantum information, where Alice encodes data through choices of bit $a_i$, basis $\alpha_i$, and intensity label $\omega_i$, while Bob employs a measurement setup featuring a beam splitter with transmittance $q$ and subsequent polarization analysis via ZZ and XX lines-each consisting of polarization beam splitters and threshold photon detectors with efficiencies $\eta_{det}$ and dark count probabilities $d$-to receive and decode the quantum signal.
A passive decoy-state BB84 protocol utilizes phase-randomized coherent states-characterized by intensity $\mu_{\omega_i}$ and polarization $\phi(a_i, \alpha_i)$-to transmit quantum information, where Alice encodes data through choices of bit $a_i$, basis $\alpha_i$, and intensity label $\omega_i$, while Bob employs a measurement setup featuring a beam splitter with transmittance $q$ and subsequent polarization analysis via ZZ and XX lines-each consisting of polarization beam splitters and threshold photon detectors with efficiencies $\eta_{det}$ and dark count probabilities $d$-to receive and decode the quantum signal.

This work provides a fully analytical, finite-key security proof for the decoy-state BB84 protocol with passive basis selection, achieving comparable key rates to active implementations.

While practical quantum key distribution (QKD) systems increasingly rely on efficient implementations, rigorous security proofs for optimized receiver designs have remained a challenge. This work, ‘Finite-key security analysis of the decoy-state BB84 QKD with passive measurement’, addresses this gap by providing a complete analytical and finite-key security analysis for the widely used BB84 protocol employing a passive basis choice at the receiver. We demonstrate that this passive measurement approach yields secret key rates comparable to those achieved with active measurement, offering practical advantages without compromising security. Does this result pave the way for simpler and more cost-effective QKD systems without sacrificing performance?

Securing Communication: The Promise of Quantum Key Distribution

Conventional encryption methods rely on mathematical complexity, meaning their security can be compromised with sufficient computing power; however, Quantum Key Distribution (QKD) offers a fundamentally different approach – information-theoretic security. This means QKD’s security isn’t based on unproven computational assumptions, but on the laws of physics themselves. QKD protocols, like BB84, leverage the principles of quantum mechanics – specifically, the uncertainty inherent in measuring quantum states – to guarantee that any attempt to eavesdrop on the key exchange will inevitably disturb the system, alerting the legitimate parties. This disturbance isn’t merely a signal of intrusion, but a physical consequence of the measurement process, ensuring that a secure key can be established even in the presence of a powerful adversary. The result is a communication channel where the confidentiality of the exchanged information is guaranteed by the very nature of reality, not by the limitations of current technology.

The BB84 protocol establishes a secure communication channel by leveraging the principles of quantum mechanics to distribute an encryption key. This method encodes information onto individual photons, utilizing four polarization states – typically 0°, 45°, 90°, and 135° – to represent bits. A sender, often termed ‘Alice’, randomly chooses both the bit value ($0$ or $1$) and the polarization basis (rectilinear or diagonal) for each photon and transmits it to a receiver, ‘Bob’. Bob independently measures each photon in a randomly chosen basis. Crucially, any attempt by an eavesdropper – ‘Eve’ – to intercept and measure the photons will inevitably disturb their quantum states, introducing detectable errors. By comparing a subset of their measurement bases through a public, but authenticated, channel, Alice and Bob can identify the presence of eavesdropping and discard compromised bits. The remaining, undisturbed bits then form a shared, secret key, guaranteed by the laws of physics, which can be used for encrypting and decrypting messages with absolute security.

While the principles of Quantum Key Distribution (QKD) promise unbreakable encryption, real-world implementations are significantly challenged by imperfections in both the communication channel and the detectors used to measure quantum signals. Photon loss, polarization drift, and background noise within optical fibers, or atmospheric turbulence in free-space links, degrade the fidelity of quantum states, introducing errors into the key exchange. Furthermore, detector vulnerabilities, such as inefficiencies in single-photon detection or susceptibility to blinding attacks, can be exploited by eavesdroppers. Consequently, a substantial body of research focuses on developing sophisticated error correction codes, characterizing detector performance, and employing advanced data analysis techniques to mitigate these practical limitations and ensure the security of QKD systems against realistic attacks. These analyses often involve complex mathematical modeling and experimental validation to quantify the impact of imperfections and establish robust security proofs for deployed QKD networks.

Key rate increases with channel transmission efficiency, reaching higher values for greater numbers of emitted pulses, as demonstrated by a comparison to the BB84 protocol.
Key rate increases with channel transmission efficiency, reaching higher values for greater numbers of emitted pulses, as demonstrated by a comparison to the BB84 protocol.

Addressing Imperfections: Enhancing QKD with Practical Solutions

The decoy-state method addresses vulnerabilities arising from imperfections in single-photon sources used in Quantum Key Distribution (QKD) systems. Traditional QKD protocols assume ideal single-photon emission, but real devices often produce multi-photon pulses, which can be exploited by intercept-resend attacks. By randomly sending weak coherent pulses with varying intensities – including zero-state (no pulse) and decoy states with attenuated pulses – the method allows estimation of key channel parameters such as the single-photon transmission probability, $Y_0$, and the multi-photon contribution. This estimation enables the legitimate parties to accurately assess the information gained by an eavesdropper, allowing them to adjust the key generation process and maintain security even with non-ideal devices. The use of decoy states effectively bounds the eavesdropper’s information, mitigating attacks that rely on exploiting the statistical properties of multi-photon emissions.

Traditional BB84 implementations require the receiver to actively choose between measurement bases. Utilizing a passive measurement basis simplifies receiver architecture by eliminating the need for active basis selection components, such as beam splitters or waveplates controlled by a random number generator. This simplification directly reduces the complexity of the receiver hardware, lowering manufacturing and operational costs. A passive basis setup typically involves a fixed polarization analyzer, enabling continuous monitoring in a single basis, and relies on post-selection of data corresponding to the correct basis as determined by the publicly discussed sifted key. This approach minimizes the number of physical components and control systems required at the receiving end, making the QKD system more practical for deployment.

The integration of decoy-state methods with passive basis selection in Quantum Key Distribution (QKD) represents a pragmatic compromise between robust security and practical implementation. Decoy-state protocols address device imperfections which can be exploited by attackers, while passive basis choice-where the receiver does not actively signal which basis is used for measurement-simplifies receiver hardware. This simplification reduces system complexity and associated costs, making deployment more feasible. The resulting system achieves a balance; it doesn’t rely on perfect, untrusted components, and it avoids the need for complex and expensive receiver technology, ultimately enabling a more readily deployable and cost-effective QKD solution without significantly compromising security guarantees.

Key rate increases with channel transmission efficiency for various numbers of emitted pulses, demonstrating performance comparable to the BB84 protocol with active polarization-encoding decoy states.
Key rate increases with channel transmission efficiency for various numbers of emitted pulses, demonstrating performance comparable to the BB84 protocol with active polarization-encoding decoy states.

Establishing Trust: Rigorous Security Proofs for QKD

A finite-key security proof for Quantum Key Distribution (QKD) systems establishes security bounds when the number of key exchanges, denoted as $n$, is limited. Unlike asymptotic proofs which assume $n$ approaches infinity, a finite-key proof directly accounts for the statistical fluctuations inherent in a finite number of exchanges. This is crucial for practical implementations where a large number of key exchanges is not always feasible or desirable. The proof determines the maximum acceptable error rate, and subsequently the secure key rate, based on parameters such as the quantum bit error rate (QBER), the number of exchanged signals, and the desired security level, ensuring confidentiality even with a restricted number of key generations.

The security of Quantum Key Distribution (QKD) systems is fundamentally tied to accurately characterizing and bounding error rates arising from imperfect detectors. Specifically, the Phase Error Rate ($P_e$) represents the probability of incorrectly determining the polarization state of a photon, while the Cross-Click Rate quantifies the probability of a single-photon detector registering a click in the absence of a signal. These rates are directly influenced by detector properties such as dark count rates, detection efficiency, and afterpulsing probability. Higher error rates reduce the final secret key length and can compromise security if not properly accounted for in the security proof. Rigorous analysis involves establishing upper bounds on these error rates, often utilizing statistical techniques and modelling of detector behavior, to ensure the derived key is secure against eavesdropping attempts.

Kato’s Inequality, a result in functional analysis, is leveraged within Quantum Key Distribution (QKD) security proofs to establish upper bounds on the probability of error occurring during key sifting. Specifically, it provides a means to bound the probability of an event based on the expected value of an operator and the norm of its commutator. In the context of QKD, this allows security analysts to relate observed error rates – such as the Quantum Bit Error Rate (QBER) – to the potential for an eavesdropper to gain information about the key. By applying Kato’s Inequality, researchers can rigorously quantify the relationship between detector imperfections, channel noise, and the ultimate security of the generated key, ensuring the mathematical soundness of the security assessment. The inequality is particularly useful when dealing with non-commutative operators that model the quantum processes involved in key distribution, allowing for precise error bounds to be derived.

This research presents a complete analytical security proof for the passive decoy-state BB84 Quantum Key Distribution (QKD) protocol. Unlike prior proofs often relying on asymptotic approximations, this work provides finite-key security estimates directly applicable to practical implementations with a limited number of key exchanges. The achieved key generation rates, calculated using the derived security bounds, are demonstrated to be comparable to those obtained with more complex active decoy-state protocols, suggesting a pathway to secure QKD systems with reduced hardware requirements and operational complexity. Specifically, the analysis details the parameters impacting key rates, including transmission distances, detector efficiencies, and error tolerances, enabling accurate performance prediction and system optimization.

Beyond Theory: Assessing Real-World Confidence in QKD

The ultimate security of a Quantum Key Distribution (QKD) system is fundamentally linked to the rate of errors occurring during photon detection and transmission. Specifically, the Dark Count Probability – the likelihood of a detector registering a photon when none is present – and the Bit Error Rate, which quantifies transmission imperfections, directly determine the achievable Security Parameter. This parameter essentially sets a lower bound on the key length needed to guarantee security against potential eavesdropping attempts. A higher Security Parameter indicates a more robust and secure key, but is inversely proportional to the acceptable error rates; thus, minimizing both dark counts and bit errors is paramount. The relationship is not merely correlational, but definitional: the Security Parameter is mathematically derived from these error sources, establishing a clear threshold beyond which the QKD system’s security can no longer be guaranteed. Consequently, advancements in detector technology and error correction protocols are crucial for extending the range and enhancing the reliability of secure quantum communication.

Quantum Key Distribution (QKD) protocols leveraging polarization encoding and single-photon detection face inherent challenges due to the linear loss channel. As photons traverse fiber optic cables, signal attenuation reduces the detection rate, limiting the effective transmission distance. Moreover, environmental factors introduce noise that can corrupt the polarization state of photons, leading to bit errors. This susceptibility is particularly problematic because single-photon detectors aren’t perfect; they exhibit a non-zero dark count rate – registering a signal even in the absence of a photon – further contributing to the error rate. The combined effect of channel loss and detector noise directly impacts the achievable key rate and ultimately, the security of the QKD system, demanding sophisticated error correction and mitigation strategies to ensure reliable and secure communication.

Quantum Key Distribution (QKD) utilizing this protocol achieves a noteworthy range of approximately 245 kilometers under practical conditions when the probability of spurious detector clicks – known as the Dark Count Probability – is minimized to $10^{-9}$. This level of performance is realized with both passive and active measurement configurations, signifying a robust system adaptable to diverse deployment scenarios. Maintaining such a low dark count rate is crucial, as it directly influences the achievable key generation rate and the overall security of the quantum communication link. The demonstrated distance indicates a viable path toward long-distance, secure communication based on the principles of quantum mechanics, offering a substantial improvement over classical cryptographic methods vulnerable to increasingly sophisticated attacks.

Investigations into Quantum Key Distribution (QKD) protocols reveal a surprising resilience to detector noise, specifically demonstrating the continued viability of passive measurement setups even with a dark count probability as high as $10^{-6}$. While ideal QKD relies on minimal noise, this research clarifies that practical implementations don’t necessarily require detectors with extremely low dark count rates to function. Though the performance metrics, such as key generation rate and transmission distance, inevitably differ from those achieved with active measurements and more sensitive detectors, passive setups offer a simpler and potentially more cost-effective approach to secure communication. This suggests that even with imperfect components, QKD can still provide a significant security advantage, broadening the potential applications of this technology.

Quantum Key Distribution (QKD) systems, while theoretically secure, are susceptible to practical imperfections that introduce errors. These errors, stemming from sources like detector dark counts and channel loss, directly compromise the achievable security level and must be systematically addressed. Thorough analysis of these error sources allows for the implementation of mitigation strategies – from optimized detector calibration to advanced error correction codes – that minimize their impact on the quantum bit error rate. By precisely quantifying and reducing these imperfections, a higher level of confidence in the system’s security can be established, ensuring the generated key is truly random and protected against eavesdropping attempts. Ultimately, diligent error mitigation is not merely a technical refinement, but a fundamental requirement for the practical deployment of robust and trustworthy QKD networks.

The pursuit of optimized quantum key distribution, as demonstrated in this analysis of the decoy-state BB84 protocol, echoes a broader tendency toward technical refinement without sufficient consideration of underlying principles. Every bias report is society’s mirror; here, the emphasis on achieving comparable key rates to active implementations, while showcasing practical advantages like passive measurement, subtly prioritizes efficiency over a holistic evaluation of security implications. As Paul Dirac once stated, “I have not the slightest idea of what I’m doing.” This seemingly paradoxical sentiment underscores the inherent limitations of any system built upon incomplete understanding, even within the rigorously defined framework of quantum mechanics. The protocol’s security, though analytically proven for finite keys, remains contingent upon assumptions about the implementation and the adversary’s capabilities-a reminder that formal verification does not equate to absolute safety.

What’s Next?

The demonstrated equivalence between active and passive decoy-state BB84 implementations, while a pragmatic step, does not resolve the fundamental tension inherent in all quantum key distribution systems. Security proofs, however rigorous, remain anchored to assumptions about device imperfections – assumptions that increasingly strain credulity as implementations approach scale. The analytical finite-key analysis presented here offers a clearer, if not complete, accounting of those limitations, but it merely refines the question, not answers it. The pursuit of ‘practical’ QKD risks prioritizing engineering expediency over genuine security guarantees.

Future work will likely concentrate on closing the device-independent QKD gap – a goal that demands not simply better detectors or more complex error correction, but a fundamental rethinking of how trust is established in a cryptographic system. The focus should shift from proving the security of a device to verifying the security despite the device. Data itself is neutral, but models reflect human bias, and increasingly sophisticated models require increasingly sophisticated scrutiny.

Ultimately, the value of this research, and indeed the entire field, will not be measured in key rates or transmission distances, but in a broader recognition that tools without values are weapons. The question is not merely can a secure key be distributed, but at what cost, and to what end?

Original article: https://arxiv.org/pdf/2511.21253.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2025-11-27 15:37