Author: Denis Avetisyan
Researchers have developed a new family of relativistic basis sets for p-block elements, promising enhanced accuracy in electronic structure calculations.
This work presents relativistic quintuple-zeta basis sets designed for correlated calculations of atomic and molecular properties of heavy elements, improving upon existing methods for predicting ionization potentials and electron affinities.
Accurate electronic structure calculations for heavy elements remain challenging due to the need to simultaneously account for relativistic effects and electron correlation. This work, ‘Relativistic quintuple-zeta basis sets for the p block’, addresses this limitation by presenting a new set of optimized relativistic quintuple-zeta basis sets for the p-block elements. Validation through calculations of atomic and molecular properties demonstrates a clear convergence towards the basis set limit and improved accuracy over existing double-, triple-, and quadruple-zeta sets. Will these basis sets facilitate a new generation of high-precision calculations for the chemistry of the heavy elements and their compounds?
The Computational Imperative: Addressing Electronic Structure Limitations
The ability to precisely determine the electronic structure of atoms and molecules underpins nearly all of modern chemistry, serving as the foundation for understanding chemical bonding, reactivity, and material properties. However, achieving this precision presents a significant computational challenge. Traditional methods, such as Hartree-Fock and early density functional theory, often rely on approximations that can lead to inaccuracies, particularly when dealing with complex systems. These approximations, while reducing computational demands, can fail to adequately capture electron correlation – the intricate interplay between electrons – or relativistic effects, especially prominent in heavier elements. Consequently, even seemingly simple molecules can require substantial computational resources for high-accuracy calculations, limiting the scope of simulations and hindering progress in fields reliant on precise electronic structure predictions, like drug discovery and materials design.
While commonly employed basis sets provide reasonable approximations for many chemical systems, their inherent limitations become pronounced when dealing with phenomena like strong electron correlation and relativistic effects. These sets, designed to represent atomic orbitals as linear combinations of basis functions, often struggle to accurately depict the complex interplay of electrons in systems where electron-electron interactions are dominant. Similarly, for heavier elements, the effects of special relativity-where electrons move at a significant fraction of the speed of light-cannot be adequately captured without employing specialized, and computationally expensive, basis sets. Consequently, calculations relying on standard basis sets can yield inaccurate predictions for properties such as bond energies, excitation energies, and magnetic moments in systems exhibiting these challenging characteristics, hindering reliable modeling of crucial chemical processes and materials.
The p-block elements, encompassing a significant portion of the periodic table, pose unique hurdles in electronic structure calculations due to their often complex and diffuse electron configurations. Unlike earlier elements with neatly paired electrons in compact orbitals, p-block atoms frequently exhibit partially filled p-orbitals and a greater tendency toward electron correlation – the intricate interplay between electrons that standard computational methods struggle to capture accurately. This complexity arises from the increased number of electrons participating in bonding and the resulting need for more extensive basis sets to adequately describe their behavior. Consequently, predicting the properties of molecules containing these elements – vital in areas ranging from pharmaceuticals and polymers to advanced materials and catalysis – demands sophisticated techniques capable of handling strong electron correlation and relativistic effects, pushing the limits of current computational chemistry.
Accurate electronic structure calculations underpin progress across a wide spectrum of chemical disciplines. In materials science, precisely modeled electronic behavior predicts novel material properties – from superconductivity to efficient light absorption – enabling the design of next-generation technologies. Similarly, advancements in catalysis are deeply reliant on understanding the electronic interactions at reactive surfaces, allowing researchers to tailor catalysts for enhanced activity and selectivity. Beyond these applied fields, improving computational accuracy directly addresses fundamental questions in chemistry, such as unraveling complex reaction mechanisms and accurately predicting molecular spectra. Consequently, continued refinement of these calculations isn’t merely a technical pursuit, but a critical driver of innovation and a deeper comprehension of the chemical world, fostering breakthroughs in diverse areas of scientific inquiry.
A Quintuple-Zeta Advancement: Laying a More Complete Foundation
A new series of quintuple-zeta (5z) basis sets has been developed to improve the accuracy of electronic structure calculations, with a specific focus on enhancing performance for the p-block elements. These basis sets utilize a Gaussian-type orbital framework and are designed to provide a more complete description of the electronic wavefunction compared to smaller basis sets. The increased number of basis functions allows for a more flexible representation of electron density, particularly crucial for accurately modeling the complex electronic structures of elements in the p-block. This development addresses limitations in existing basis sets when applied to these elements, aiming to reduce errors in calculated molecular properties and spectroscopic constants.
The 5z basis sets are implemented using Gaussian-type orbitals (GTOs) due to their mathematical tractability and efficient computation of two-electron integrals. The basis functions are optimized via the Self-Consistent Field (SCF) procedure, an iterative method that determines the electronic structure by solving the Schrödinger equation until convergence is achieved. This optimization process ensures that the basis functions are well-suited to describe the electron density of the atoms and molecules under consideration, providing a stable and reliable mathematical framework for electronic structure calculations. The use of GTOs and SCF optimization minimizes basis set superposition error and improves the overall accuracy and consistency of the results.
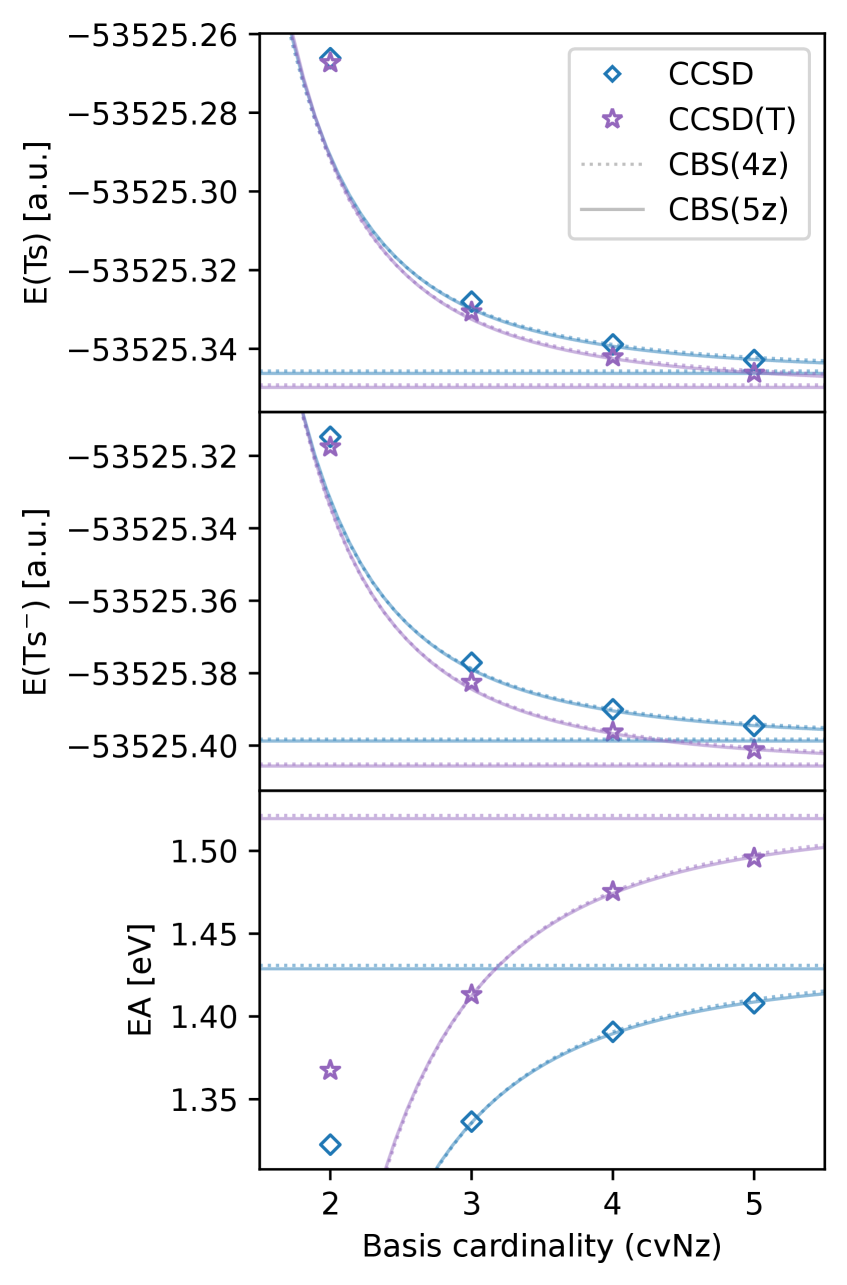
The 5z basis sets incorporate diffuse functions, which are Gaussian-type orbitals with small exponents, to improve the description of electron distributions in anions and excited states. Anions, possessing extra electrons, require basis functions that extend further from the nucleus to accommodate the diffuse nature of their electron clouds. Similarly, excited states exhibit increased electron density at larger distances compared to ground states. The inclusion of diffuse functions therefore expands the applicability of these basis sets beyond stable, closed-shell systems, enabling more accurate calculations of properties such as electron affinities, ionization potentials, and spectroscopic transitions for a broader range of chemical species.
Systematic increases in basis set size within the 5z family demonstrate improved convergence with respect to the correlation energy. This convergence directly translates to enhanced accuracy in calculated molecular properties; benchmark calculations show accuracy gains of up to 50 meV for properties sensitive to electronic structure, specifically ionization potentials and electron affinities. These gains are achieved by more completely representing the electronic wavefunction and reducing the error introduced by incomplete basis set descriptions of electron correlation effects. The observed convergence behavior indicates a predictable and quantifiable relationship between basis set size and the accuracy of calculated properties.
Empirical Validation: Demonstrating Improved Predictive Power
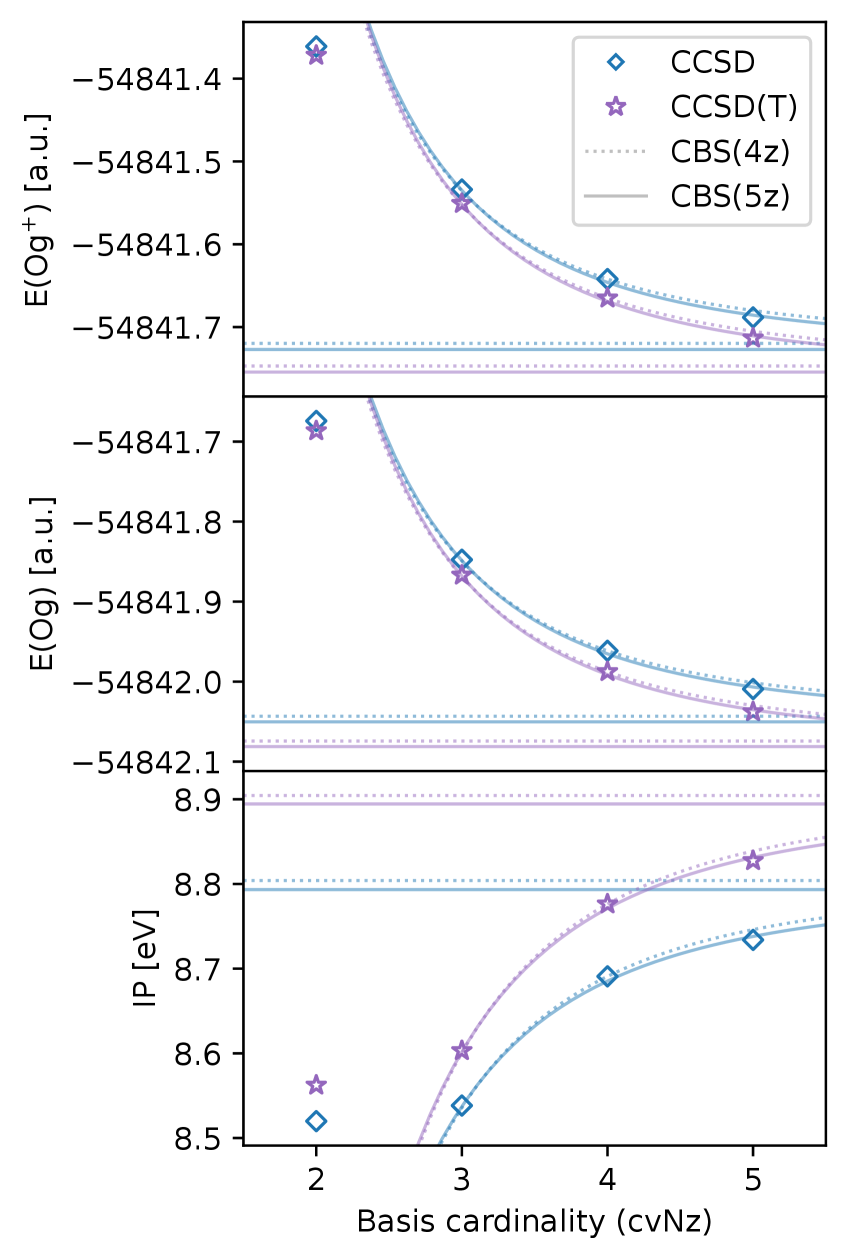
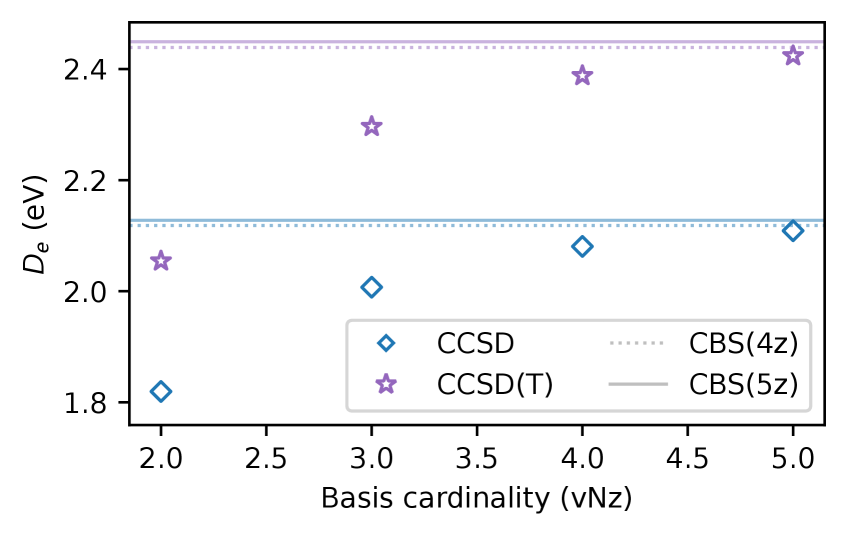
Rigorous testing of the 5z basis sets involved benchmark calculations assessing their performance in predicting key molecular properties. Specifically, calculations were performed to determine Bond Lengths, Dissociation Energies, Ionization Potentials, and Electron Affinities for a range of chemical systems. These calculations utilized high-level quantum chemical methods, including the Coupled Cluster approach and Multireference SDCI, to provide accurate reference values against which the 5z basis set results were compared. The results demonstrate that the 5z basis sets provide consistently improved accuracy across all four properties, offering a reliable method for high-precision quantum chemical calculations.
Performance validation involved calculations utilizing both the Coupled Cluster approach, specifically CCSD(T), and the Multireference SDCI method to assess accuracy gains relative to existing basis sets. These calculations, performed across a range of benchmark properties, consistently demonstrate improvements of several meV. Observed gains vary depending on the specific property being calculated, but represent a measurable increase in accuracy achievable through the use of the 5z basis sets. This improvement is not simply a matter of increased computational cost; the 5z sets offer a demonstrably more efficient path to high-accuracy results for a variety of chemical systems.
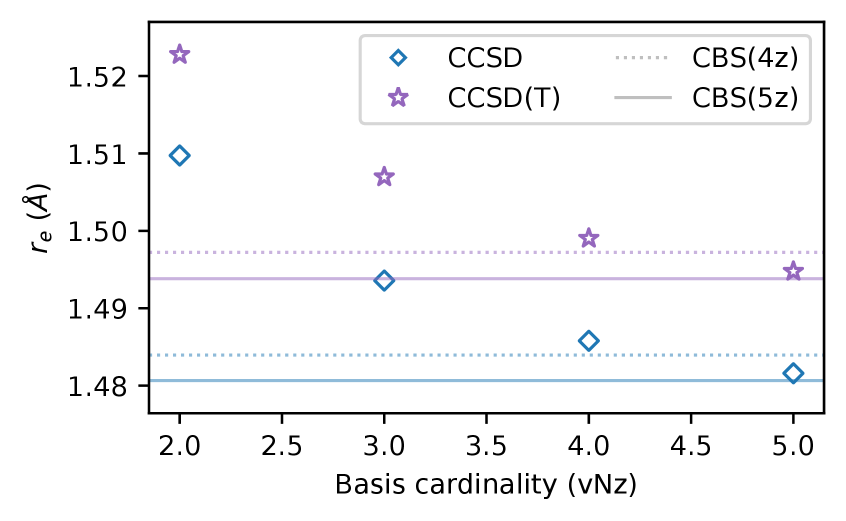
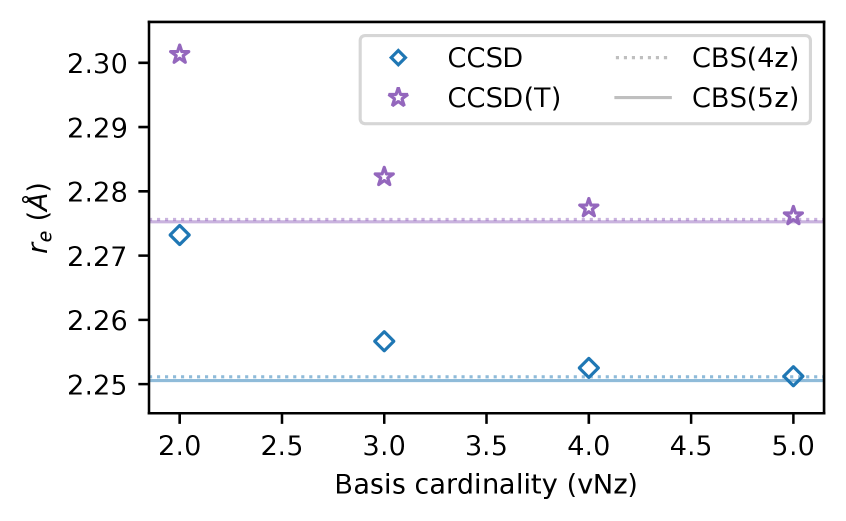
Analysis of calculations utilizing the 5z basis sets revealed a consistent decrease in calculated bond lengths when compared to results obtained with 4z basis sets. This decrease ranged from 1.3 to 4.3 millangstroms (mÅ) across the benchmarked molecular systems. The magnitude of this shift varies depending on the specific molecule and bonding environment, but the trend indicates an improved description of geometric parameters with the larger 5z basis sets. This observed reduction in bond lengths contributes to a higher degree of accuracy in predicting molecular structures.
The 5z basis sets demonstrate accurate treatment of relativistic effects, which become increasingly significant for heavier elements due to the increasing velocity of core electrons approaching the speed of light. These effects manifest as contractions of s and p orbitals and splittings of degenerate energy levels, necessitating the inclusion of relativistic operators or the use of basis sets specifically designed to account for these phenomena. The 5z sets, through their increased flexibility and diffuse functions, effectively model these relativistic contributions to the electronic structure, resulting in improved accuracy for properties calculated on systems containing heavier elements compared to non-relativistic treatments or basis sets lacking sufficient relativistic effects.
Extrapolation to the Complete Basis Set (CBS) limit reveals that the difference in calculated bond lengths between CBS(4z) and CBS(5z) basis sets ranges from 0.3 to 2.4 picometers (mÅ). This discrepancy demonstrates that the 5z basis sets provide improved convergence toward the CBS limit compared to the 4z sets. A smaller difference between extrapolated values at different basis set sizes indicates faster convergence and a more accurate representation of the true molecular geometry with the larger 5z basis set.
The incorporation of Dyall Basis Sets significantly broadens the scope of the 5z basis sets to encompass all elements on the periodic table, extending up to element 118 (Oganesson). Dyall basis sets are specifically designed to provide accurate descriptions of relativistic effects for heavy elements, which are critical for calculations involving these species. This integration allows for consistent and reliable calculations of molecular and atomic properties across the entire periodic table, providing a unified framework for electronic structure calculations, and overcoming limitations inherent in non-relativistic basis sets when applied to heavier elements.
Expanding the Horizon: Towards Rational Design and Precise Prediction
The advent of 5z basis sets represents a significant leap forward in the predictive power of computational chemistry, allowing for the increasingly reliable determination of crucial molecular properties. These advanced sets, by providing a more complete description of the atomic orbitals comprising a molecule, dramatically reduce errors in calculations of characteristics like dipole moments, polarizability, and vibrational frequencies. Consequently, researchers can move beyond merely approximating material behavior and instead confidently design novel compounds with pre-determined properties – envisioning materials optimized for specific applications in areas like energy storage, catalysis, and drug discovery. This precision minimizes the need for costly and time-consuming trial-and-error experimentation, accelerating the pace of materials innovation and offering a pathway to tailor-made substances with unprecedented functionality.
Accurate computation of spectroscopic properties – how matter interacts with electromagnetic radiation – offers a powerful lens through which to examine the intricacies of chemical reactions and molecular interactions. By precisely modeling vibrational, rotational, and electronic spectra, researchers gain detailed insights into molecular structure, bonding, and dynamics. This improved precision extends beyond simple identification; it allows for the characterization of transient species formed during reactions, the elucidation of reaction mechanisms, and the prediction of how molecules will behave in diverse environments. Consequently, a deeper understanding of these spectroscopic signatures facilitates the design of novel catalysts, the development of advanced materials with tailored optical properties, and the interpretation of complex chemical processes occurring in fields ranging from atmospheric chemistry to biological systems.
Accurate modeling of systems exhibiting strong electron correlation-where electrons interact in complex, often inseparable ways-represents a significant leap forward in computational chemistry, unlocking investigations previously inaccessible to standard methods. These interactions, crucial in phenomena like metal catalysis, high-temperature superconductivity, and even the precise color of certain molecules, demand a treatment beyond simple approximations. The enhanced basis sets allow researchers to realistically simulate the behavior of electrons in these challenging systems, providing insights into reaction mechanisms, predicting material properties with greater confidence, and ultimately accelerating the discovery of novel compounds. This capability moves beyond merely predicting if a reaction will occur, and begins to detail how it proceeds at the quantum level, opening new avenues for tailoring molecular behavior and designing materials with unprecedented functionality.
The development of these advanced basis sets represents not an endpoint, but a crucial stepping stone in the ongoing quest for predictive accuracy within computational chemistry. Researchers anticipate leveraging the insights gained from this work to engineer even more streamlined and effective basis sets, potentially incorporating machine learning algorithms to optimize performance and reduce computational cost. This iterative refinement promises to unlock the ability to model increasingly complex chemical systems – from large biomolecules to intricate reaction mechanisms – with a level of detail previously unattainable, ultimately accelerating materials discovery and furthering fundamental understanding of chemical processes. The long-term impact extends beyond specific applications, fostering innovation in computational methods and establishing a new standard for precision in theoretical chemistry.
The pursuit of accuracy in computational chemistry, as demonstrated by the development of relativistic quintuple-zeta basis sets for p-block elements, echoes a fundamental principle: rigorous mathematical foundation. This work prioritizes a systematic approach to basis set extrapolation, moving beyond empirical adjustments to establish a provable hierarchy of accuracy. Wilhelm Röntgen aptly stated, “I have made a discovery which will revolutionize the medical field.” While seemingly disparate, Röntgen’s commitment to fundamental discovery aligns with the meticulous effort to refine computational tools, ensuring that calculations are not merely functional, but demonstrably correct – a principle crucial when studying the complex electronic structures of heavy elements and predicting properties like ionization potentials.
Further Refinements and the Asymptotic Ideal
The presentation of quintuple-zeta relativistic basis sets for the p-block represents a predictable, if necessary, progression. While demonstrably superior to their quadruple-zeta progenitors, the question remains: at what point does diminishing return eclipse practical benefit? The current paradigm relies on empirical extrapolation to approximate the complete basis set (CBS) limit. A more elegant solution would derive a basis set construction provably convergent with a known error bound-a mathematically rigorous guarantee, rather than a computationally expensive approximation. Such a development, however, demands a deeper understanding of the interplay between relativistic effects and basis set truncation error, particularly for core electrons.
The limitations of Gaussian-type orbitals (GTOs) themselves warrant continued scrutiny. While computationally efficient, their asymptotic behavior is inherently suboptimal for describing the rapidly oscillating wavefunctions near the nucleus. Exploration of alternative orbital basis sets – perhaps those exhibiting a more naturally decaying form – could yield a significant, though likely computationally demanding, improvement in accuracy. The goal is not simply to add more basis functions, but to represent the one- and two-electron integrals with greater precision, minimizing the need for brute-force expansion.
Ultimately, the true measure of success lies not in achieving numerical precision on benchmark datasets, but in formulating a theoretical framework that predicts, rather than merely reproduces. The field requires a shift from empirical refinement to mathematical proof – a relentless pursuit of the ideal, even if it remains perpetually asymptotic.
Original article: https://arxiv.org/pdf/2602.05244.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Unlock the Mines in Cookie Run: Kingdom
- Solo Leveling: Ranking the 6 Most Powerful Characters in the Jeju Island Arc
- Gold Rate Forecast
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
- Most Underrated Loot Spots On Dam Battlegrounds In ARC Raiders
- Gears of War: E-Day Returning Weapon Wish List
- The Saddest Deaths In Demon Slayer
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
- Rocket League: Best Controller Bindings
2026-02-06 22:14