Predicting Patient Outcomes with Privacy and Insight

by

Author: Denis Avetisyan

A new approach leverages quantum-inspired tensor trains to build clinical prediction models that safeguard patient data without sacrificing the ability to understand how predictions are made.

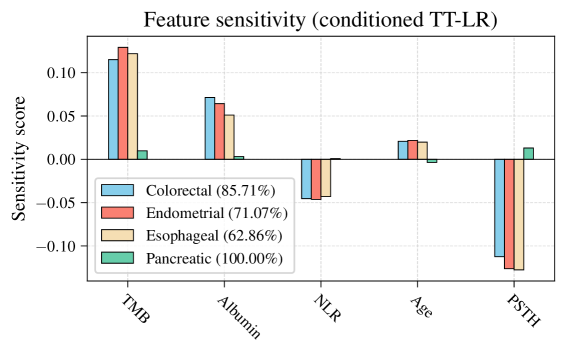
Conditioned Tensor Train-Low Rank (TT-LR) models demonstrate feature sensitivities that vary significantly across different cancer types, as evidenced by the balanced accuracy achieved for each condition-a metric reflecting the model's performance on corresponding data.
Conditioned Tensor Train-Low Rank (TT-LR) models demonstrate feature sensitivities that vary significantly across different cancer types, as evidenced by the balanced accuracy achieved for each condition-a metric reflecting the model’s performance on corresponding data.

Tensor train models offer a compelling balance between privacy protection, model interpretability, and predictive accuracy for clinical applications.

Balancing predictive power, model transparency, and data privacy remains a central challenge in clinical machine learning. The work ‘Private and interpretable clinical prediction with quantum-inspired tensor train models’ addresses this by introducing tensor trains (TTs) as a novel approach to obfuscate model parameters while preserving both accuracy and interpretability. Our results demonstrate that TTs significantly enhance privacy against membership inference attacks, achieving a privacy-utility trade-off comparable to differential privacy, yet potentially offering greater insight into model behavior through efficient computation of marginal and conditional distributions. Could this quantum-inspired technique provide a practical pathway toward truly private, interpretable, and effective clinical prediction systems?

Unveiling the Fragility of Model Privacy

Despite their remarkable capabilities, machine learning models are surprisingly susceptible to attacks that compromise the privacy of the data used to train them. These vulnerabilities stem from the model itself essentially memorizing aspects of its training data, rather than simply generalizing patterns. An adversary, through techniques like model inversion or membership inference, can query the model and, based on its responses, reconstruct sensitive information about individual data points used during training – potentially revealing personal details, confidential records, or proprietary information. This is not merely a theoretical concern; demonstrated attacks have successfully extracted data from models trained on image datasets, text corpora, and even medical records, highlighting a fundamental tension between model performance and data privacy that demands ongoing research and robust mitigation strategies.

The vulnerability of machine learning models extends across varying levels of access, presenting a complex privacy challenge. In a black-box scenario, attackers with no knowledge of the model’s internal workings can still infer sensitive information from its outputs through repeated queries – effectively reverse-engineering the training data. Conversely, white-box attacks, where the model’s parameters and architecture are fully exposed, allow for even more direct extraction of private details. This duality necessitates the development of privacy safeguards that are resilient to both types of threats; techniques effective against black-box attacks may prove insufficient when faced with a fully exposed model, and vice versa. Consequently, a multi-faceted approach to privacy is crucial, moving beyond single solutions to encompass defenses tailored to the specific access conditions and attack vectors a model might encounter.

Efforts to safeguard data privacy within machine learning models frequently encounter a fundamental challenge: a demonstrable reduction in model performance. Techniques like differential privacy and data anonymization, while aiming to obscure individual contributions to the training dataset, often introduce noise or information loss. This inevitably impacts the model’s accuracy, generalizability, and overall utility – creating a precarious trade-off between privacy preservation and practical effectiveness. The extent of this performance degradation varies based on the specific method employed, the sensitivity of the data, and the complexity of the model itself, but it remains a persistent hurdle in deploying privacy-conscious machine learning systems. Researchers are actively exploring innovative approaches to minimize this utility loss, seeking methods that offer strong privacy guarantees without significantly compromising the model’s predictive power.

Median balanced accuracy reveals that models trained on individual public datasets perform differently than those trained on combined datasets including each public dataset.
Median balanced accuracy reveals that models trained on individual public datasets perform differently than those trained on combined datasets including each public dataset.

Compressing for Confidentiality: Reducing the Attack Surface

Model compression techniques mitigate privacy risks by reducing the attack surface available to adversaries. Larger, more complex models possess a greater capacity to memorize sensitive training data, increasing the potential for extraction attacks such as model inversion or membership inference. By decreasing the number of parameters and overall model size through methods like pruning, quantization, or knowledge distillation, the amount of information an attacker can potentially extract is limited. This reduction in model complexity restricts the attacker’s ability to reconstruct training data or infer individual data points used during model training, thereby enhancing privacy guarantees. The effectiveness of this approach is directly correlated with the degree of compression achieved and the specific compression algorithm employed.

Tensor Train Decomposition (TTD) is a model compression technique that represents a tensor – a multi-dimensional array of parameters common in machine learning models – as a product of smaller tensors, or “trains”. This decomposition reduces the total number of parameters required to represent the model, achieving compression. Importantly, the resulting train tensors can be individually analyzed, offering potential for enhanced interpretability by allowing researchers to identify which parameters contribute most significantly to model outputs. The efficiency of TTD is linked to the rank, or size, of these constituent tensors; lower ranks yield greater compression but may sacrifice accuracy if the decomposition cannot effectively represent the original model. The method is applicable to various model architectures, including convolutional neural networks and recurrent neural networks, and has demonstrated promise in reducing model size without substantial performance degradation.

The effectiveness of model compression using Tensor Train Decomposition is directly correlated to the ability to accurately represent the original model’s weights and biases with a minimized set of Tensor Train coefficients. This representation involves decomposing higher-order tensors into a series of lower-order tensors, effectively reducing the number of parameters required. The quality of this approximation is determined by the rank, or ‘T’, used in the Tensor Train decomposition; higher ranks allow for greater representational capacity but reduce compression, while lower ranks increase compression at the potential cost of accuracy. Successful compression relies on selecting an appropriate rank ‘T’ that balances model size reduction with acceptable performance degradation, ensuring the resulting model retains sufficient information to maintain its intended functionality and prevent significant loss of predictive power.

Both linear regression (LR) and tensor train (TT) models reveal feature sensitivities, quantified by normalized coefficients for LR and marginalization for TT, demonstrating comparable sensitivity scales despite differing calculation methods.
Both linear regression (LR) and tensor train (TT) models reveal feature sensitivities, quantified by normalized coefficients for LR and marginalization for TT, demonstrating comparable sensitivity scales despite differing calculation methods.

Benchmarking Privacy: Establishing a Baseline with Logistic Regression

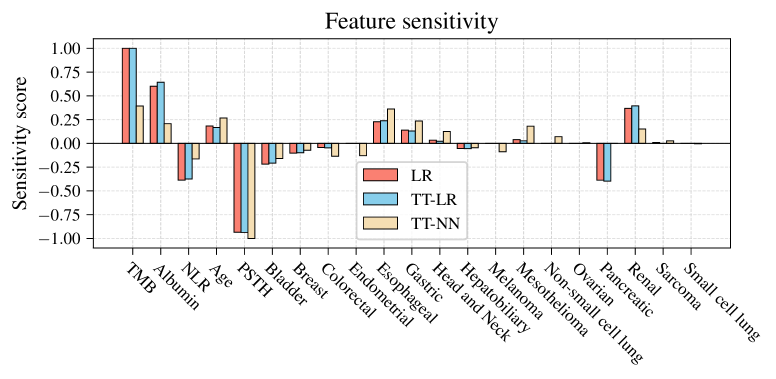
The Loris model, a Logistic Regression implementation, serves as the foundational benchmark against which the privacy-preserving capabilities of Tensor Train Decomposition are assessed. Logistic Regression was selected due to its established performance in binary classification tasks relevant to the dataset and its computational efficiency, facilitating rapid experimentation and comparison. The model is trained on the same dataset used for evaluating the Tensor Train Decomposition, utilizing identical data preprocessing steps – specifically, standardization – to ensure a fair and unbiased evaluation of privacy gains. Performance is measured by comparing the Attack Accuracy (Hamming Score), Balanced Accuracy, and Area Under the Receiver Operating Characteristic Curve (AUC) of the Loris model against the compressed Tensor Train models, quantifying the trade-off between privacy and utility.

Data standardization is a necessary preprocessing step prior to model training to prevent feature scaling disparities from influencing model performance and ensuring a valid comparison between the Loris (Logistic Regression) baseline and the Tensor Train (TT) compressed models. This process involves transforming each feature to have zero mean and unit variance, effectively normalizing the data distribution. Without standardization, features with larger scales could disproportionately impact the Logistic Regression’s coefficient estimation and subsequent performance metrics, leading to biased results. Applying standardization consistently to both the baseline and compressed models mitigates this effect, allowing for a more accurate assessment of the privacy-utility trade-offs achieved through TT decomposition, and isolates the impact of the compression technique itself on model accuracy and attack resilience.

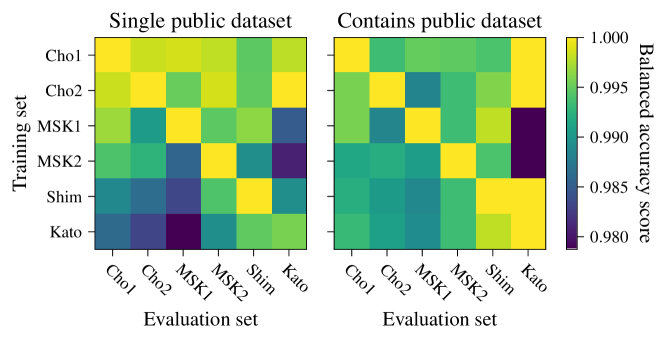
Cross-validation was implemented to generate robust and statistically significant performance estimates for both the baseline Logistic Regression model (Loris) and the Tensor Train Decomposition models. A k-fold cross-validation scheme was utilized, dividing the dataset into k mutually exclusive subsets. The models were trained on k-1 folds and evaluated on the remaining fold, repeating this process k times to ensure each fold served as a validation set once. Metrics including Attack Accuracy (Hamming Score), Balanced Accuracy, and Area Under the Curve (AUC) were then averaged across all folds, providing a less biased and more reliable assessment of model performance compared to a single train/test split. This approach is critical for establishing the validity of comparisons between models with and without privacy-enhancing techniques and for quantifying the trade-off between privacy and utility.

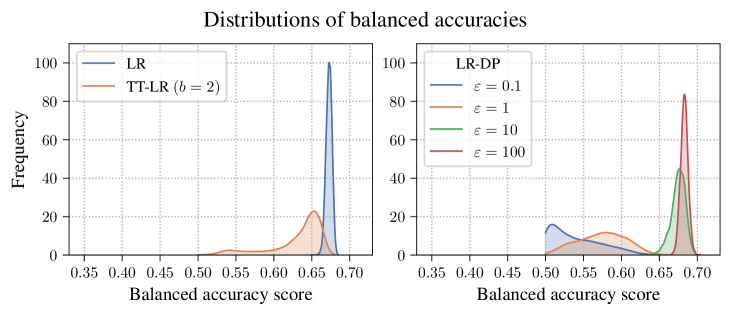
Tensor Train (TT) decomposition, when applied as a privacy mechanism, results in an Attack Accuracy, measured by the Hamming Score, of 0.5 or lower. This performance level is statistically comparable to that achieved by Differential Privacy implementations utilizing small epsilon (ε) values. Conversely, models trained without privacy-preserving techniques demonstrate significantly higher Attack Accuracy, consistently approaching 1.0, indicating a substantial vulnerability to attacks aimed at reconstructing private data. The Hamming Score quantifies the fraction of correctly identified private attributes, and a reduction to ≤ 0.5 represents a meaningful improvement in privacy protection without a commensurate loss in model utility, as demonstrated by balanced accuracy and AUC metrics.

Tensor Train (TT) models, while designed to enhance privacy, demonstrate a preservation of predictive utility comparable to non-private models. Evaluation metrics, specifically Balanced Accuracy and Area Under the Curve (AUC), reveal statistically similar performance between the TT models and those trained without privacy constraints. This indicates that the application of TT decomposition does not substantially degrade the model’s ability to accurately classify data or distinguish between classes, suggesting a minimal trade-off between privacy protection and model usefulness. These results are critical, as maintaining utility is a primary requirement for the practical deployment of privacy-enhancing technologies.

Analysis revealed a substantial increase in the ability to identify a specific subgroup, designated ‘Kato’, when privacy-preserving measures were absent. Without protections, the attack success rate – the probability of correctly identifying members of the Kato subgroup within the broader training dataset – rose from approximately 0.5, representing performance at chance level, to nearly 1.0, indicating near-certain identification. This demonstrated a significant vulnerability in the absence of privacy mechanisms and underscores the necessity of techniques such as Tensor Train decomposition to mitigate such risks and protect sensitive subgroup information.

Vanilla models trained on Cho1 demonstrate varying balanced accuracy across all datasets, as shown by the distribution of results.
Vanilla models trained on Cho1 demonstrate varying balanced accuracy across all datasets, as shown by the distribution of results.

Towards Robust Intelligence: Implications and Future Directions

Machine learning systems are increasingly vulnerable to data breaches and adversarial attacks, raising significant concerns about security and trust. Tensor Train Decomposition presents a promising solution by fundamentally altering how models are structured and trained. This technique efficiently compresses model parameters – often reducing storage requirements by orders of magnitude – while simultaneously making them more resistant to manipulation. When coupled with methods like Differential Privacy, which adds carefully calibrated noise to the training data, the risk of sensitive information leakage is dramatically reduced. The combined effect isn’t simply about safeguarding data; it fosters a new paradigm where models are inherently more robust, interpretable, and trustworthy, paving the way for wider adoption in sensitive applications such as healthcare and finance. This approach moves beyond traditional security measures by embedding privacy and resilience directly into the model’s architecture, offering a proactive defense against evolving threats.

The convergence of privacy, compression, and interpretability represents a significant advancement in machine learning model design. Traditionally, these aspects have been treated as competing priorities – powerful models often sacrifice transparency and data security. However, techniques leveraging methods like Tensor Train Decomposition demonstrate that it’s possible to achieve all three simultaneously. By reducing model complexity through compression, and incorporating differential privacy mechanisms, these systems not only safeguard sensitive information but also become more readily understood by researchers and end-users. This trifecta of benefits paves the way for building trustworthy artificial intelligence, enabling responsible deployment in critical applications where both performance and accountability are paramount, and fostering greater public confidence in these increasingly pervasive technologies.

While Tensor Train Decomposition shows promise in enhancing machine learning security and efficiency, a crucial next step involves rigorously testing its scalability with increasingly complex architectures, particularly deep Neural Networks. Current studies often focus on smaller datasets or simplified models; extending this approach to the vast parameter spaces characteristic of modern networks presents significant computational challenges. Future research must address these hurdles, investigating methods to optimize the decomposition process and minimize the trade-offs between compression, privacy, and model accuracy at scale. Successfully navigating these complexities could unlock the potential for truly trustworthy and efficient AI systems capable of handling real-world data with enhanced security and interpretability.

The pursuit of both predictive power and model transparency, as demonstrated in this work with tensor trains, echoes a fundamental principle of sound system design. This paper effectively navigates the privacy-utility trade-off, revealing that a carefully constructed model-one that prioritizes elegant representation like the use of tensor trains-can offer robust performance without sacrificing the ability to understand its internal logic. Grace Hopper famously said, “It’s easier to ask forgiveness than it is to get permission.” This resonates with the spirit of innovation shown here; the researchers didn’t shy away from exploring a novel approach to address the critical need for privacy in clinical prediction. Good architecture is invisible until it breaks, and only then is the true cost of decisions visible.

What Lies Ahead?

The pursuit of predictive modeling in clinical settings inevitably encounters the brittle boundaries between utility and privacy. This work, leveraging the structure of tensor trains, offers a compelling, if not entirely surprising, demonstration that elegant compression can provide a meaningful defense against membership inference attacks. The performance achieved suggests a pathway beyond the often-onerous constraints of differential privacy, but it also illuminates a critical point: the defense isn’t inherent in the algorithm, but in the reduction of degrees of freedom.

Future work must address the limitations inherent in any compression technique. The ideal model isn’t merely accurate and private, but also robust to distribution shift-a challenge that tensor trains, in their current form, do not inherently solve. Further exploration is needed into the interplay between TT-rank, model complexity, and generalization error. The system’s behavior will be dictated by how these factors interact.

Ultimately, the true test lies not in achieving marginal gains in privacy-utility trade-offs, but in building systems that anticipate failure modes. Structure dictates behavior, and the weaknesses will reside along the invisible boundaries of the model’s representation. The most fruitful research will focus on methods for identifying – and proactively addressing – those vulnerabilities before they manifest as systemic failures.

Original article: https://arxiv.org/pdf/2602.06110.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-09 20:44