Predicting Solid-State Stability: A Benchmark for Advanced Density Functionals

Author: Denis Avetisyan

A new study rigorously tests the accuracy of modern density functional theory methods in predicting the structural behavior of group IV elements like silicon and germanium.

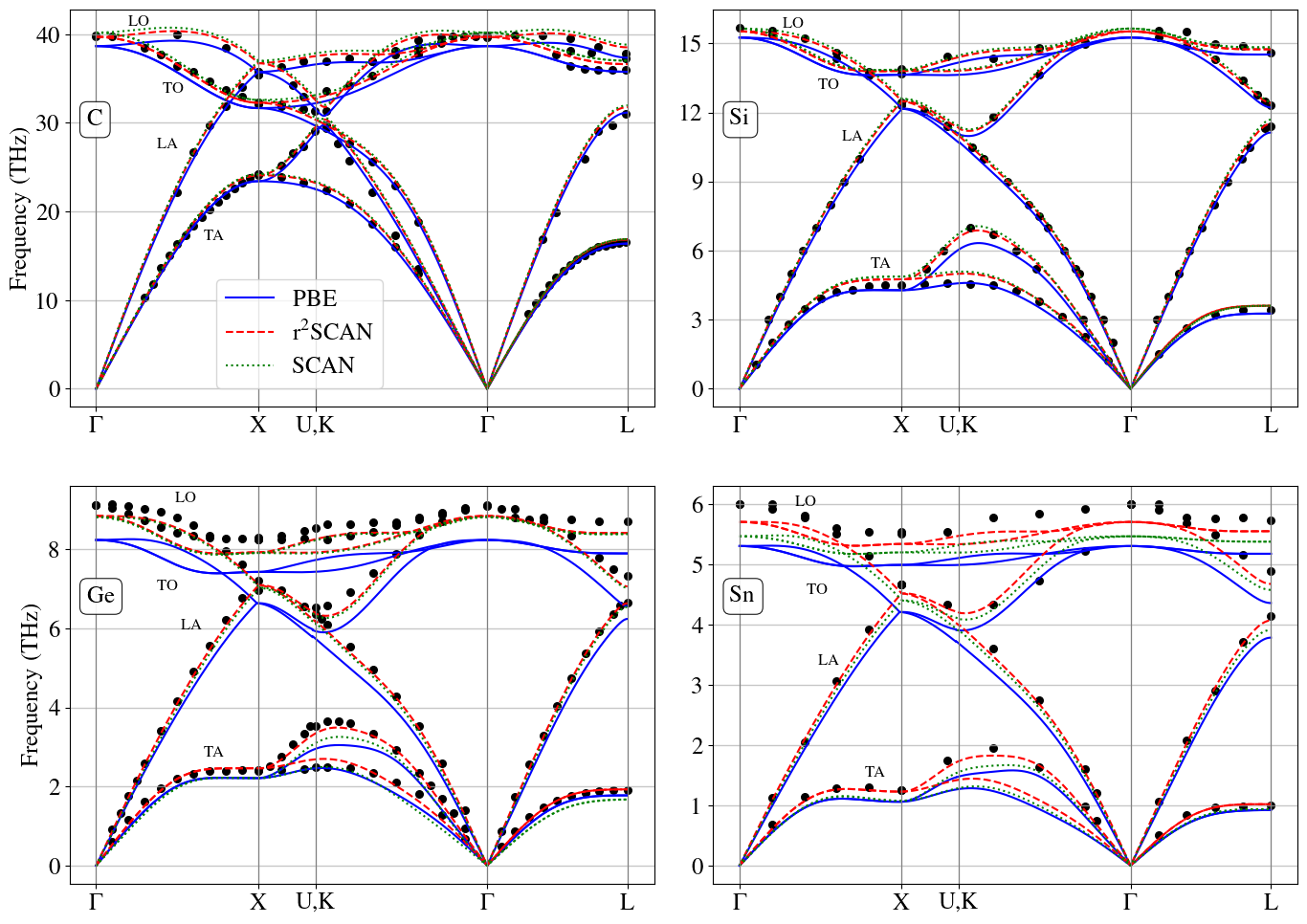
The study demonstrates that density functional theory, utilizing the PBE, r2SCAN, and SCAN functionals, accurately reproduces the experimentally verified phonon dispersion relations for diamond-structured group IV elements - carbon, silicon, germanium, and tin - thereby validating the predictive power of these methods for modeling lattice dynamics in these materials and providing a theoretical foundation for understanding their thermal properties. — The study demonstrates that density functional theory, utilizing the PBE, r2SCAN, and SCAN functionals, accurately reproduces the experimentally verified phonon dispersion relations for diamond-structured group IV elements – carbon, silicon, germanium, and tin – thereby validating the predictive power of these methods for modeling lattice dynamics in these materials and providing a theoretical foundation for understanding their thermal properties.

Researchers evaluate the performance of PBE, SCAN, and r2SCAN meta-GGAs for calculating elastic properties, phonon dispersion, and phase transition pressures in group IV elemental solids.

Accurate materials modeling relies on the delicate balance between computational cost and predictive power in exchange-correlation functionals. This study, ‘Lattice dynamics and structural phase stability of group IV elemental solids with the r$^2$SCAN functional’, benchmarks the recently revised r$^2$SCAN meta-GGA functional against its predecessor, SCAN, and conventional approximations for predicting the elastic properties and phase stability of carbon, silicon, germanium, and tin. While r$^2$SCAN generally improves upon the PBE functional and demonstrates comparable performance to SCAN for many properties, we find it significantly overestimates transition pressures for germanium and tin. Does this discrepancy suggest limitations in r$^2$SCAN’s treatment of subtle energetic landscapes governing structural phase transitions, and what adjustments might improve its accuracy?

The Elegance of Density: Foundations and Limitations

Density Functional Theory (DFT) has become a foundational technique within materials science, offering a computationally efficient means of predicting a vast range of material properties directly from the fundamental laws of quantum mechanics. Unlike methods that explicitly solve the many-body Schrödinger equation – often intractable for all but the simplest systems – DFT focuses on the electron density, a much simpler quantity, to determine a material’s ground state energy and, consequently, its behavior. This “first principles” approach, meaning predictions are based solely on physical constants and the atomic numbers of the constituent elements, allows researchers to model materials with unprecedented accuracy, guiding the discovery of novel compounds and optimizing existing ones for applications ranging from superconductivity and catalysis to energy storage and advanced electronics. The broad applicability and relative ease of implementation have cemented DFT’s position as an indispensable tool for both theoretical investigation and practical materials design.

While Density Functional Theory (DFT) has become indispensable for modeling materials, standard approximations like the Local Density Approximation (LDA) exhibit limitations when applied to strongly correlated systems. These systems, characterized by significant electron-electron interactions, defy accurate prediction using LDA because the approximation struggles to capture the complex many-body effects governing their behavior. In materials with strong correlation, such as certain transition metal oxides or f-electron systems, electrons are not independent entities but are highly influenced by each other’s presence, leading to phenomena like Mott insulating behavior or unconventional superconductivity. Consequently, LDA often produces inaccurate results for these materials, misrepresenting their electronic structure, magnetic properties, and overall stability – highlighting the need for more sophisticated approaches to account for these intricate interactions.

The predictive power of Density Functional Theory, while substantial, is fundamentally limited by approximations made in calculating the exchange-correlation energy – a term representing the complex interactions between electrons. Standard implementations often fail to fully address the issue of electron self-interaction, where each electron spuriously interacts with itself, leading to inaccurate energy estimations and flawed predictions of material behavior. Furthermore, capturing the intricacies of electron correlation – the collective behavior arising from the mutual repulsion of electrons – proves exceptionally challenging. These limitations are particularly pronounced in strongly correlated systems, where electron interactions dominate and simple approximations break down, necessitating more sophisticated – and computationally expensive – methods to achieve reliable results. Addressing these deficiencies remains a central focus in the ongoing development of more accurate and robust density functional methods.

Gradient and Meta-GGA Functionals: Refining the Approximation

Generalized Gradient Approximation (GGA) functionals represent an advancement over the Local Density Approximation (LDA) in density functional theory by accounting for the non-homogeneity of the electron density. LDA approximates the exchange-correlation energy at a given point solely based on the electron density at that point. GGAs, however, incorporate the gradient of the electron density $\nabla\rho(\mathbf{r})$ into the exchange-correlation functional, allowing for a more accurate description of systems where the electron density varies significantly. This inclusion addresses limitations of LDA in describing bonding, predicting molecular geometries, and calculating excitation energies, as the gradient provides information about the rate of change of the electron density and thus a better representation of the electron distribution.

Meta-GGA functionals represent an advancement over Generalized Gradient Approximation (GGA) density functionals by incorporating the kinetic energy density, or the Laplacian of the density, into the exchange-correlation calculations. This inclusion allows meta-GGAs, such as the Strongly Constrained and Appropriately Normed (SCAN) functional, to satisfy a larger number of known exact constraints that govern electron behavior. Specifically, SCAN is designed to satisfy all 17 known exact constraints, leading to improved accuracy in predicting molecular geometries, vibrational frequencies, and barrier heights compared to both LDA and GGA functionals. The increased adherence to these fundamental constraints enhances the transferability of the functional, meaning it performs more reliably across a wider range of chemical systems and properties.

The Exchange Gradient Expansion (XGE) is a perturbative approach used in density functional theory (DFT) to systematically improve upon the local density approximation (LDA). It expands the exchange-correlation energy as a series in terms of the gradient of the electron density $\nabla \rho(\mathbf{r})$ . This expansion allows for the construction of increasingly accurate functionals, such as Generalized Gradient Approximations (GGAs) and meta-GGAs, by including higher-order gradient corrections. The XGE provides a formal framework for deriving these functionals, though practical implementation requires truncation of the series and the introduction of approximations to ensure numerical stability and computational feasibility. Functionals derived through the XGE, particularly those satisfying known exact constraints, demonstrate improved accuracy in predicting ground-state properties compared to LDA.

Charge density difference maps, calculated as <span class="katex-eq" data-katex-display="false"> \Delta n(\mathbf{r})=n\_{\rm r^{2}SCAN}}(\mathbf{r})-n\_{\rm SCAN}}(\mathbf{r}) </span>, reveal variations in electronic structure across the α and β phases of Si, Ge, and Sn, with blue/dark regions indicating positive charge accumulation and light/white regions indicating depletion, visualized in the (0<span class="katex-eq" data-katex-display="false"> \bar{1} </span>1) and (110) planes with atomic nuclei and nearest-neighbor bonds shown. — Charge density difference maps, calculated as $\Delta n(\mathbf{r})=n\_{\rm r^{2}SCAN}}(\mathbf{r})-n\_{\rm SCAN}}(\mathbf{r})$ , reveal variations in electronic structure across the α and β phases of Si, Ge, and Sn, with blue/dark regions indicating positive charge accumulation and light/white regions indicating depletion, visualized in the (0 $\bar{1}$ 1) and (110) planes with atomic nuclei and nearest-neighbor bonds shown.

Validation and Implementation: Establishing Computational Rigor

Accurate density functional theory (DFT) calculations are critically dependent on the treatment of core electrons. Methods employing pseudopotentials, while computationally efficient, can introduce spurious effects due to the approximation of the core electron potential. All-electron methods, such as the Projector Augmented Wave (PAW) method, explicitly include the contributions from all electrons, including core electrons, thereby minimizing these artifacts. The PAW method achieves this by representing the electronic wavefunction in two forms: one smooth everywhere and another confined to the core region, allowing for accurate calculations of material properties without the limitations inherent in pseudopotential approaches.

Benchmarking density functional theory (DFT) functionals requires rigorous comparison of computationally derived material properties against established experimental data or high-level theoretical results. For evaluating functional reliability, properties such as elastic constants-which describe a material’s resistance to deformation-and phonon dispersion-representing the vibrational modes of the lattice-are particularly informative for solids. Accurate prediction of these properties indicates the functional’s ability to correctly represent the electronic structure and interatomic interactions governing material behavior. A comprehensive benchmarking process, applied consistently across a range of materials, provides a statistically significant basis for assessing a functional’s transferability and identifying potential limitations for specific material classes.

The r2SCAN meta-GGA functional offers a compelling balance of accuracy and computational cost when applied to Group IV elemental solids (Carbon, Silicon, Germanium, and Tin). Specifically, calculations utilizing r2SCAN achieve levels of precision in predicting material properties comparable to those obtained with the Heyd-Scuseria-Ernzerhof (HSE) hybrid functional, which incorporates a portion of exact exchange. Importantly, r2SCAN accomplishes this performance while retaining the computational efficiency characteristic of semilocal density functional theory (DFT) approximations, avoiding the significant expense associated with hybrid functionals like HSE. This makes r2SCAN a practical alternative for studying the structural and electronic properties of these materials, particularly in scenarios where computational resources are limited or large-scale calculations are required.

Validation of the r2SCAN functional included calculating the transition pressure for Silicon, resulting in a value of 13.7 GPa. This calculated value demonstrates strong agreement with experimental data, which reports a transition pressure of 13.0 GPa when Zero-Point Expansion corrections are applied. This close correspondence supports the reliability of r2SCAN in accurately predicting the behavior of Silicon under pressure and provides a benchmark for assessing its performance with other materials.

Analysis of phase transitions within Group IV elemental solids revealed a systematic overestimation of transition pressures for Germanium and Tin when utilizing the r2SCAN functional. While r2SCAN accurately predicted the transition pressure for Silicon at 13.7 GPa, closely aligning with experimental values of 13.0 GPa (following Zero-Point Expansion corrections), calculations for Germanium and Tin yielded significantly higher pressures, indicating a potential limitation in the functional’s transferability to heavier elements within this material class. This discrepancy suggests that the underlying approximations within r2SCAN may not adequately capture the complex electronic behavior of Germanium and Tin under pressure, necessitating further investigation or functional refinement for accurate prediction of their high-pressure properties.

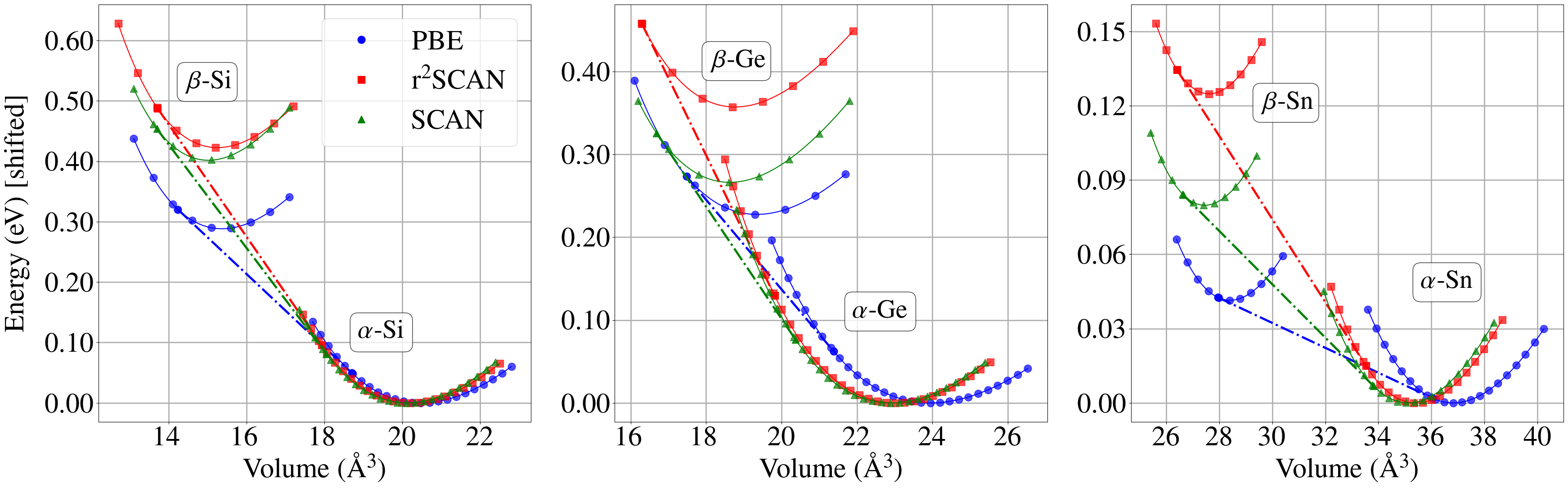
Calculations using PBE, r2SCAN, and SCAN functionals reveal energy-volume relationships for α and β phases of Si, Ge, and Sn, with transition pressures determined from the intersection of the phase curves and detailed in Table 5.

Towards Predictive Materials Science: A Future Defined by Accuracy

The Revised SCAN (rSCAN) meta-GGA functional represents a significant refinement of the original SCAN functional, addressing limitations in numerical stability that previously hindered its application to certain materials and systems. While SCAN already offered improvements over traditional exchange-correlation functionals by satisfying all 17 known exact constraints, rSCAN further optimizes the functional form to ensure more robust performance across a broader range of chemical environments. This enhancement is achieved through a modified parameterization that minimizes the likelihood of unphysical behavior during electronic structure calculations, particularly in systems with strong electronic correlations or complex bonding arrangements. Consequently, rSCAN not only provides more reliable predictions for materials already accessible to SCAN, but also extends the scope of accurate density functional theory calculations to previously intractable systems, paving the way for advancements in diverse fields like catalysis, energy storage, and materials design.

Hybrid functionals, such as the Heyd-Scuseria-Ernzerhof (HSE) functional, represent a significant refinement in density functional theory by strategically incorporating a fraction of exact Hartree-Fock exchange. This addition directly addresses the persistent issue of self-interaction error, a common artifact in approximate exchange-correlation functionals where an electron spuriously interacts with itself. By blending the strengths of density functional theory – its computational efficiency – with the accuracy of Hartree-Fock exchange, HSE and similar functionals offer a more balanced approach. This careful combination often leads to improved predictions of material properties, including band gaps, magnetic moments, and structural energies, ultimately enhancing the reliability of computational materials science and accelerating the design of novel materials with targeted characteristics.

The culmination of recent developments in density functional theory empowers materials scientists with an unprecedented ability to forecast how materials will behave. This predictive power isn’t merely about confirming existing knowledge; it actively accelerates the entire materials discovery process, drastically reducing the reliance on costly and time-consuming trial-and-error experimentation. Researchers can now virtually screen thousands of potential material compositions, identifying promising candidates with specifically desired characteristics – from high-temperature superconductivity to enhanced catalytic activity – before ever synthesizing a single sample. Consequently, the design of materials with tailored properties – optimized for applications ranging from energy storage and conversion to advanced electronics and structural components – transitions from an artful endeavor to a precise, computationally guided science, promising innovations across diverse technological landscapes.

The pursuit of accurate material modeling, as demonstrated in this study of group IV elemental solids, demands a rigorous adherence to first principles. The investigation into functionals like r2SCAN, while showing improvements over PBE, highlights the subtle balance required in defining exchange-correlation energy. It echoes a sentiment expressed by Isaac Newton: “I have not been able to discover the composition of any mixed body, though I have been able to discover the composition of the purest.” Just as Newton sought fundamental truths in matter, this work dissects the intricacies of density functional theory, acknowledging that even refined approximations-like r2SCAN’s tendency to overestimate transition pressures-require continuous refinement to approach true predictive power. The emphasis on phonon dispersion and elastic properties exemplifies this dedication to a mathematically pure understanding of material behavior.

Future Directions

The persistent challenge in computational materials science remains not merely predicting stability, but proving it. This work, while demonstrating r2SCAN’s refinement over PBE and even SCAN, reveals a troubling tendency: a systematic overestimation of transition pressures. This is not a failure of the functional itself, but a stark reminder that empirical parameterizations, however sophisticated, are fundamentally approximations. A functional that perfectly reproduces known structures is not necessarily a functional that correctly predicts all structures, or even avoids pathological behavior in unexplored chemical spaces.

The path forward necessitates a shift in emphasis. Rather than endlessly tweaking parameters to fit existing data, greater effort must be devoted to constructing functionals with a solid theoretical foundation. Proof of correctness, derived from first principles, should supersede reliance on benchmark datasets. The development of genuinely non-empirical functionals, or at least those with rigorously quantifiable error bounds, is paramount. The continued pursuit of accuracy through brute-force fitting will yield diminishing returns; elegance – and true predictive power – lies in mathematical purity.

Ultimately, the true test of any functional will not be its performance on germanium or tin, but its ability to correctly predict the behavior of materials yet to be synthesized – materials existing only as solutions to the Schrödinger equation. Until computational materials science embraces a more formal, proof-based methodology, it will remain, at best, a highly sophisticated form of informed guesswork.

Original article: https://arxiv.org/pdf/2601.11177.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

The Elegance of Density: Foundations and Limitations

Gradient and Meta-GGA Functionals: Refining the Approximation

Validation and Implementation: Establishing Computational Rigor

Towards Predictive Materials Science: A Future Defined by Accuracy

Future Directions

See also: