Quantization’s New Twist: Mass Diffusion for More Efficient AI

by

Author: Denis Avetisyan

A novel framework optimizes the compression of large language models by strategically reordering data before quantization, dramatically improving accuracy and reducing computational costs.

MixQuant optimizes quantization by initially reordering weights and activations to distribute activation mass evenly across blocks, then rotating these permuted tensors, and finally rounding them to a target alphabet determined by bit width, scaling, and zero point-a process designed to minimize information loss during the conversion to lower precision.
MixQuant optimizes quantization by initially reordering weights and activations to distribute activation mass evenly across blocks, then rotating these permuted tensors, and finally rounding them to a target alphabet determined by bit width, scaling, and zero point-a process designed to minimize information loss during the conversion to lower precision.

MixQuant leverages permutation equivariance and Hadamard rotations to suppress outliers and achieve state-of-the-art post-training quantization performance.

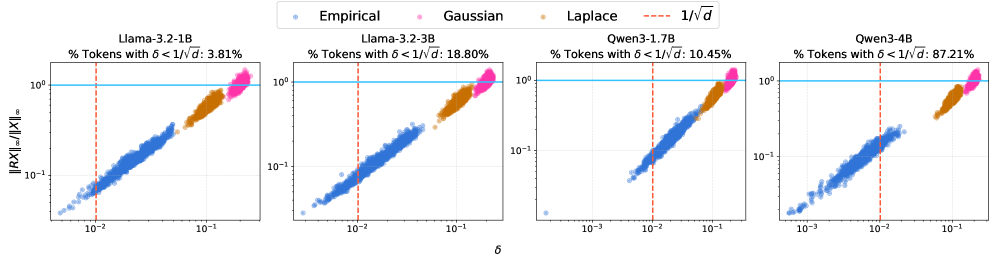
While recent advances in post-training quantization (PTQ) leverage block rotations to mitigate the impact of outliers, the fundamental limitations of this approach remain poorly understood. This work, ‘MixQuant: Pushing the Limits of Block Rotations in Post-Training Quantization’, presents a non-asymptotic analysis revealing that effective outlier suppression is intrinsically linked to the distribution of activation mass within blocks. Guided by these insights, we introduce MixQuant, a framework that strategically permutes activations to equalize blockwise \ell_1 norms prior to rotation, recovering up to 90% of full-vector rotation accuracy when quantizing Llama3 1B to INT4. Can these permutation-aware techniques unlock further improvements in the efficiency and performance of increasingly large language models?

The Cost of Scale: Addressing LLM Complexity

Large Language Models have demonstrated an unprecedented ability to generate human-quality text, translate languages, and answer complex questions – capabilities that promise to revolutionize fields ranging from customer service to scientific research. However, this power comes at a considerable cost: these models are extraordinarily large, often containing billions of parameters. This immense size presents a significant hurdle to widespread deployment, particularly on edge devices or in resource-constrained environments. The substantial memory footprint and computational demands of LLMs necessitate powerful hardware and considerable energy consumption, limiting their accessibility and increasing operational expenses. Consequently, researchers are actively exploring methods to reduce model size without sacrificing performance, seeking to unlock the full potential of these transformative technologies for a broader range of applications.

Post-training quantization represents a crucial strategy for deploying large language models (LLMs) on resource-constrained devices and infrastructure. This technique fundamentally reduces a model’s memory footprint and computational demands by representing its weights and activations with fewer bits – typically transitioning from 32-bit floating-point numbers to 8-bit integers or even lower precisions. The resulting compression directly translates to substantial savings in storage space and faster processing speeds, enabling LLMs to run efficiently on edge devices or within tighter budgetary constraints. While the process doesn’t require retraining the model – hence “post-training” – careful implementation is necessary to minimize the inevitable accuracy loss associated with reduced numerical precision, making it a central focus of ongoing research and optimization efforts.

The reduction of an LLM’s precision-often termed quantization-while promising substantial efficiency gains, introduces a critical challenge: accuracy degradation. As models transition from high-precision formats like 32-bit floating point to lower bit-widths – such as 8-bit integer or even less – information is inevitably lost. This loss manifests as quantization error, a discrepancy between the original, full-precision value and its reduced representation. Aggressive quantization, pushing to extremely low bit-widths, amplifies this error, leading to noticeable declines in the model’s ability to correctly process information and generate accurate outputs. The core issue lies in the limited capacity of fewer bits to represent the full spectrum of values within the model’s weights and activations, effectively creating a coarser approximation of the original data and hindering the model’s nuanced understanding of language.

Addressing the performance loss inherent in compressing Large Language Models necessitates innovative approaches to information preservation within the constraints of reduced precision. Current research explores techniques beyond simple rounding, such as mixed-precision quantization – strategically allocating higher bit-widths to critical model parameters – and quantization-aware training, which fine-tunes the model to be inherently robust to the errors introduced by lower precision. Another promising avenue involves advanced coding schemes that intelligently distribute quantization error, minimizing its impact on key activations and weights. These methods aim to retain the essential information encoded within the model’s parameters, effectively bridging the gap between computational efficiency and sustained accuracy, and allowing deployment on resource-constrained devices without sacrificing the quality of generated text or completed tasks.

This quantization graph architecture maintains all rotations online while merging permutations and quantizing weights and activations in linear layers, as described in [3].
This quantization graph architecture maintains all rotations online while merging permutations and quantizing weights and activations in linear layers, as described in [3].

Outlier Suppression: The Foundation of Stable Quantization

Quantization error is not uniformly distributed across activation values; extreme values, or outliers, contribute a disproportionately large share of the overall error. This is due to the limited precision of low-bit quantization, where a relatively small change in a large activation value results in a significant quantization error. The magnitude of this error is further amplified during backpropagation, impacting gradient accuracy and potentially destabilizing training. Consequently, even a small percentage of outlier activations can significantly degrade the performance of a quantized neural network, necessitating specific techniques for their mitigation. The impact is not linear; the error contribution increases exponentially with the outlier’s magnitude, making outlier suppression a critical component of successful quantization.

Low-bit quantization reduces model size and computational cost, but introduces quantization error due to the limited number of representable values. This error is not uniformly distributed; extreme values, or outliers, within activation vectors contribute disproportionately to the overall quantization error. Consequently, suppressing these outliers is critical for maintaining acceptable accuracy levels when employing low-bit quantization techniques. Failure to adequately address outliers results in a significant degradation in model performance, as the quantization process struggles to accurately represent these values with a reduced bit-width. Therefore, strategies specifically designed to minimize the impact of outlier activations are essential components of successful low-bit quantization pipelines.

Hadamard Rotation and Mass Diffusion are techniques employed to mitigate the impact of outlier activations during quantization. Hadamard Rotation applies a Hadamard transform to activation vectors, effectively spreading the energy concentrated in a few dimensions across all dimensions. Mass Diffusion, conversely, directly redistributes activation mass by applying a learned or fixed matrix to the activations. Both methods aim to reduce the magnitude of extreme values by diffusing their influence, thereby lessening the quantization error that arises from representing these high-magnitude activations with a limited number of bits. This redistribution doesn’t alter the overall information content, but rather changes the distribution of values to be more amenable to low-bit quantization, resulting in improved model accuracy.

Analyzing the distribution of activation values within defined blocks allows for the identification of potential outlier issues during quantization. Specifically, high concentrations of both activation mass – the proportion of values within a block – and activation energy – typically measured as the sum of squared values – indicate a disproportionate influence from a small number of activations. This concentration suggests that these activations will contribute heavily to quantization error after bit-width reduction. Techniques can then be applied to these identified blocks, such as clipping, scaling, or more sophisticated redistribution methods, to mitigate the impact of outliers and improve overall model accuracy with low-bit quantization. The degree of concentration, often quantified using statistical measures like variance or entropy within a block, serves as a reliable indicator for prioritizing outlier suppression efforts.

Analysis of activation distributions from the Llama3 1B model reveals that increasing the block size <span class="katex-eq" data-katex-display="false">b</span> in Hadamard rotation reduces outlier suppression, as demonstrated by the decreasing activation range in configurations (a)-(d).
Analysis of activation distributions from the Llama3 1B model reveals that increasing the block size b in Hadamard rotation reduces outlier suppression, as demonstrated by the decreasing activation range in configurations (a)-(d).

Block Hadamard Rotation: An Optimized Strategy for Efficiency

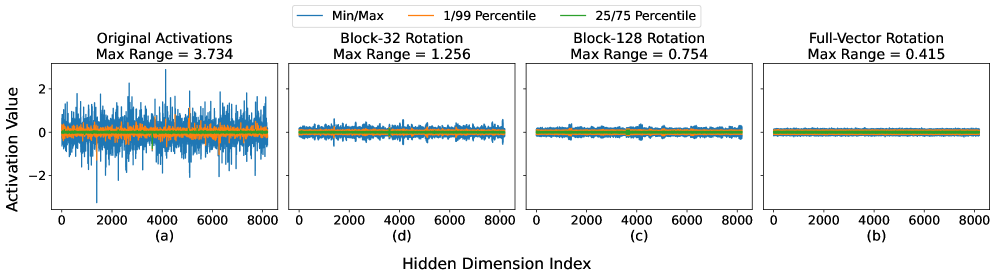
Full-vector rotation, a technique for optimizing neural network performance, involves applying a rotation matrix to the entire activation vector at each layer. While demonstrably effective in improving accuracy, this method exhibits significant computational cost due to the high dimensionality of these vectors, particularly in large language models. The computational complexity scales linearly with the vector dimension, making full-vector rotation impractical for deployment in resource-constrained environments or at scale. The matrix multiplication required for each rotation becomes a bottleneck, increasing latency and energy consumption during inference and training.

Block Hadamard Rotation optimizes computational efficiency by shifting from full-vector rotation to operating on fixed-size blocks of the activation vector. Instead of applying a rotation matrix to the entire vector, this method divides the vector into blocks, typically of size 16, and performs the rotation on each block independently. This decomposition significantly reduces the number of computations required, as the complexity scales with the block size rather than the full vector dimension. The technique leverages the permutation-equivariant properties of the network to minimize information loss during this block-wise processing, enabling a practical trade-off between accuracy and computational cost.

The efficiency gains of Block Hadamard Rotation are predicated on the existence of permutation-equivariant regions within neural networks. Permutation equivariance implies that the network’s output remains unchanged when the order of input elements is altered, specifically within these regions. This property allows for rotation operations to be applied to blocks of activations without disrupting the network’s overall function. Consequently, computations can be performed on these blocks as a unit, significantly reducing the number of individual rotation operations required compared to full-vector rotation, while largely preserving representational capacity due to the inherent symmetry within the permutation-equivariant space.

Block Hadamard Rotation enhances computational efficiency by applying rotational transformations to fixed-size blocks within the activation vector, rather than to the full vector. This block-wise operation effectively mitigates the impact of outlier values and reduces quantization error, which typically degrade performance in lower-precision models. Experimental results using the MixQuant implementation demonstrate that, with a block size of 16, this approach recovers approximately 90% of the accuracy achieved by full-vector rotation for the Llama3 1B parameter model, 88% for the 3B model, and 83% for the 8B model, indicating a substantial preservation of performance despite the computational optimizations.

MixQuant streamlines transformer feedforward networks by substituting full-vector rotations with permutation and block rotation, enabling weight merging for inference while retaining necessary online rotations despite the non-rotation-equivariant nature of the Swish activation.
MixQuant streamlines transformer feedforward networks by substituting full-vector rotations with permutation and block rotation, enabling weight merging for inference while retaining necessary online rotations despite the non-rotation-equivariant nature of the Swish activation.

Towards Efficient and Accurate Quantization: Expanding the Boundaries

Quantization, the process of reducing a model’s precision, inevitably introduces error; however, recent advancements demonstrate substantial mitigation through careful management of activation distributions and the application of optimized rotation techniques. These methods reshape the data flowing through the neural network, ensuring a more uniform distribution that minimizes information loss during the reduction in precision. By strategically rotating the weight matrices, the algorithms effectively align the activations, thereby decreasing the magnitude of quantization errors that typically accumulate in high-dimensional spaces. This nuanced approach not only preserves model accuracy but also unlocks the potential for significantly compressing large language models, making deployment feasible on devices with limited computational resources and memory.

The capacity to significantly compress large language models (LLMs) unlocks possibilities for their deployment on devices with limited computational resources and memory. Previously confined to data centers and high-end hardware, LLMs can now operate effectively on smartphones, embedded systems, and edge computing platforms. This expansion is achieved through techniques that reduce the precision of model weights and activations, thereby minimizing storage requirements and accelerating inference speeds. The resultant highly compressed models retain a surprising degree of accuracy, enabling a broader range of applications, including real-time language translation, personalized virtual assistants, and offline access to powerful AI capabilities – all without relying on constant cloud connectivity. This democratization of LLM technology promises to bring sophisticated AI-driven experiences to a much wider audience and foster innovation across diverse fields.

Quantization algorithms, crucial for deploying large language models on devices with limited resources, experience significant performance gains when coupled with optimized activation manipulation strategies. Algorithms such as Qronos and GPTQ, designed to reduce model size and accelerate inference, directly benefit from techniques that carefully manage the distribution of activations within the neural network. These optimizations minimize the information loss inherent in the quantization process, enabling more accurate and efficient compression. By strategically altering activations before quantization, these algorithms can reduce outlier impacts and improve overall model fidelity, ultimately leading to substantial improvements in both speed and accuracy for a given bit-width.

The pursuit of increasingly compact large language models has led to innovations in quantization techniques, notably the adoption of 4-bit floating-point formats like MXFP4. This approach significantly reduces model size with minimal impact on performance, enabling deployment on devices with limited resources. Recent advancements, such as the MixQuant algorithm, have demonstrably narrowed the performance gap between these streamlined quantization methods and more computationally intensive full-vector rotations, particularly with block sizes of 128 or greater. MixQuant achieves this through a reduction in the influence of outlier activations, thereby stabilizing the quantization process and preserving model accuracy despite the extreme compression. This targeted mitigation of outlier impact represents a crucial step towards efficient and accurate model quantization, paving the way for broader accessibility of powerful language models.

Analysis of activations from Llama3 and Qwen3 models using WikiText2 reveals that while most tokens exceed the <span class="katex-eq" data-katex-display="false">1/\sqrt{d}</span> threshold predicted by Proposition 1, consistent range reduction is observed and strongly correlates with δ, suggesting that the observed range reduction is not simply due to random sampling from standard Gaussian or Laplacian distributions.
Analysis of activations from Llama3 and Qwen3 models using WikiText2 reveals that while most tokens exceed the 1/\sqrt{d} threshold predicted by Proposition 1, consistent range reduction is observed and strongly correlates with δ, suggesting that the observed range reduction is not simply due to random sampling from standard Gaussian or Laplacian distributions.

The pursuit of efficient large language models necessitates a relentless distillation of complexity. MixQuant embodies this principle, demonstrating how strategic permutation-equalizing mass prior to block Hadamard rotations-yields substantial gains in both accuracy and computational efficiency. This focus on outlier suppression, achieved through refined activation manipulation, aligns with a core tenet of simplification. As Blaise Pascal observed, “The eloquence of the body is to be seen, not heard.” Similarly, MixQuant prioritizes demonstrable performance-reduced overhead and improved accuracy-over superfluous computational layers. Clarity, in this instance, is the minimum viable kindness.

What Remains?

The pursuit of efficient large language models invariably leads to simplification. MixQuant’s strategic application of permutation and rotation offers a refinement, not a resolution. The framework addresses outlier suppression, a persistent nuisance, but sidesteps the fundamental question of representation. Reducing computational overhead is a tangible benefit, yet the underlying matrices still demand attention. The elegance of Hadamard transforms, while appealing, is not a panacea; future work must consider the limitations imposed by strict orthogonality.

A natural progression lies in exploring adaptive permutation strategies. Current methods rely on fixed block sizes; a dynamic approach, responsive to the data’s intrinsic structure, might yield further gains. Beyond rotation, other transformation families deserve scrutiny. The focus on permutation equivariance, while commendable, should not overshadow the potential benefits of breaking that symmetry when appropriate. Perhaps the true path lies not in minimizing information loss, but in intelligently discarding what is irrelevant.

Ultimately, MixQuant represents a step towards a leaner model, but it is merely a single iteration. The field should resist the temptation to accumulate complexity. The ideal remains a model that achieves sufficient accuracy with minimal intervention-a model where the hand of the author has vanished, leaving only the inherent structure of the data to speak for itself.

Original article: https://arxiv.org/pdf/2601.22347.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-02 15:24