Author: Denis Avetisyan
A new quantum algorithm dramatically accelerates the estimation of critical failure probabilities in complex engineering systems, offering a significant advantage over traditional methods.
This paper introduces a stabilized maximum-likelihood iterative quantum amplitude estimation (ML-IQAE) technique for efficiently calculating Conditional Value-at-Risk (CVaR) in structural reliability analysis under correlated random fields.
Accurate quantification of tail risk in complex structural systems remains computationally challenging due to high-dimensional uncertainty. This is addressed in ‘Stabilized Maximum-Likelihood Iterative Quantum Amplitude Estimation for Structural CVaR under Correlated Random Fields’ through a novel quantum-enhanced framework for estimating Conditional Value-at-Risk (CVaR). The proposed method leverages iterative quantum amplitude estimation with a stabilized inference scheme to achieve a quadratic oracle-complexity advantage over classical Monte Carlo methods while maintaining rigorous statistical reliability. Could this approach unlock efficient and robust risk assessment for increasingly complex engineering designs and beyond?
The Illusion of Certainty: Quantifying Risk in Complex Systems
Effective engineering design and safety evaluations across disciplines-from civil infrastructure and aerospace to nuclear power and environmental science-depend heavily on robust risk assessment. This frequently necessitates calculating the expected value of a performance metric when that metric is influenced by a random field-a quantity that varies continuously across space with interdependencies between nearby points. Consider, for instance, predicting the structural integrity of a bridge given spatially varying wind loads, or assessing the likelihood of groundwater contamination stemming from uncertain soil permeability. These scenarios involve estimating integrals over high-dimensional probability distributions defined on the random field, a computationally intensive task. The challenge isn’t simply dealing with randomness, but with the spatial correlation-the fact that values at nearby locations are statistically linked-which dramatically increases the complexity of the calculation and often pushes traditional Monte Carlo methods beyond practical limits.
Estimating risk across spatially correlated fields presents a significant computational hurdle for conventional methods, especially as problem dimensionality increases. The challenge isn’t simply the volume of data, but how that data is interconnected; each point’s value influences its neighbors, creating a web of dependencies that multiplies the necessary calculations. Traditional techniques, such as Monte Carlo simulation, require an exponentially growing number of samples to maintain accuracy as the number of variables rises, quickly becoming intractable for realistic, high-dimensional scenarios. This computational burden limits the ability to perform timely and accurate risk assessments in fields like civil, mechanical, and environmental engineering, where complex systems demand robust predictions under uncertainty. Consequently, researchers are actively pursuing novel approaches to reduce computational cost without sacrificing the fidelity of these critical estimations.
The fundamental challenge in quantifying risk across spatially correlated fields arises from the sheer complexity of representing and managing inherent uncertainty. Conventional methods, often reliant on discretizing the field and performing Monte Carlo simulations, quickly become computationally prohibitive as the dimensionality increases. This is because the number of samples required to accurately capture the dependencies between variables grows exponentially with the number of dimensions. Consequently, propagating uncertainty through engineering models – determining how variations in the field translate to variations in system performance – demands an impractically large computational burden. Researchers are therefore focused on developing techniques – such as reduced-order models and polynomial chaos expansion – that can efficiently approximate the field’s probability distribution and circumvent the limitations of traditional approaches, enabling reliable risk assessment even for highly complex systems.
A Quantum Glimmer: Estimating Risk with Iterative Amplitude Estimation
The Iterative Quantum Amplitude Estimation (IQAE) algorithm is designed for the efficient estimation of Conditional Value at Risk (CVaR), specifically addressing challenges presented by spatially correlated random fields. Unlike traditional methods, IQAE leverages quantum computation to accelerate the CVaR estimation process. The algorithm is structured to iteratively refine the estimated CVaR value, improving accuracy with each iteration. This approach is particularly beneficial when dealing with high-dimensional, correlated data sets common in financial risk management and other quantitative applications, where classical Monte Carlo simulations can be computationally expensive and time-consuming.
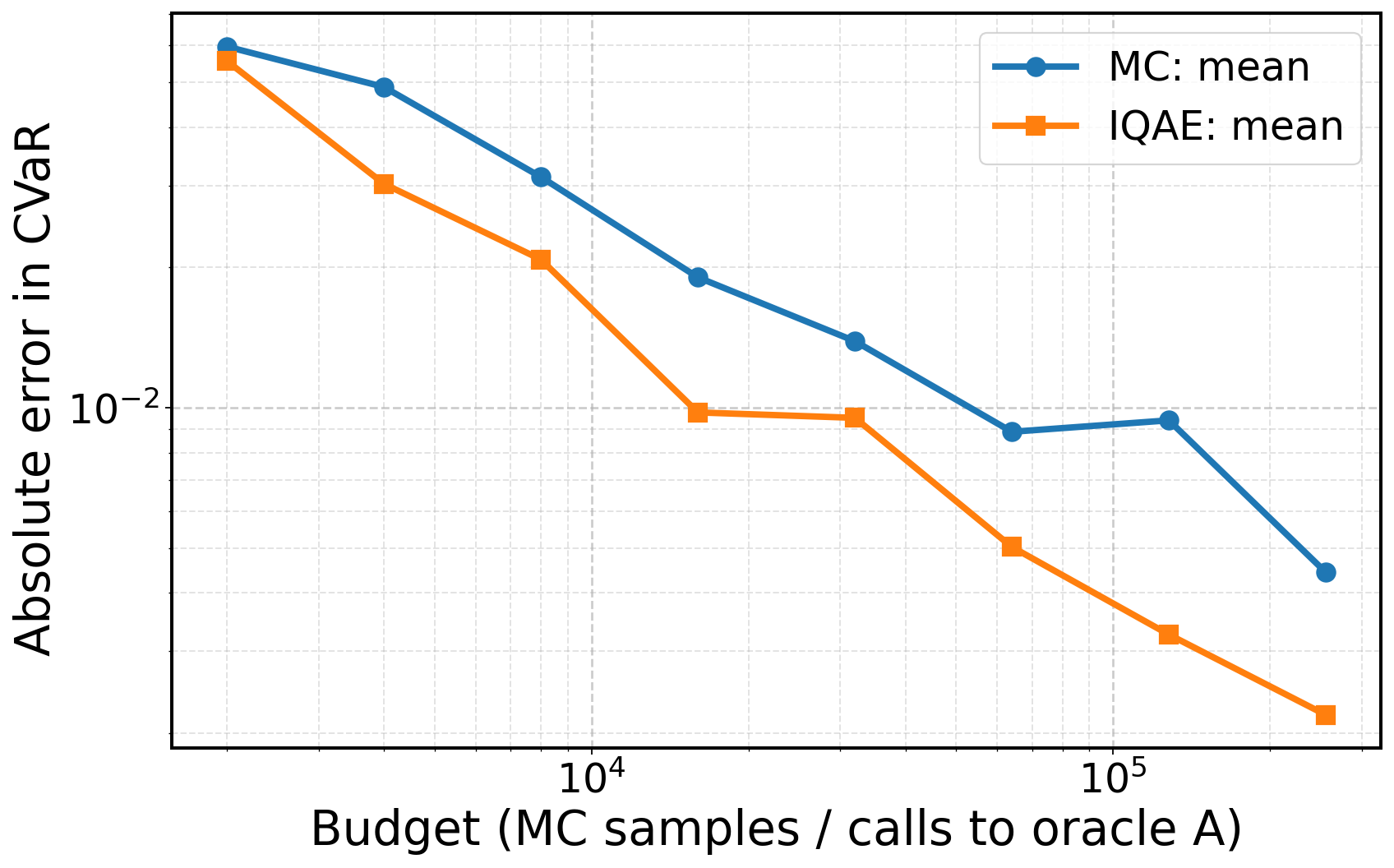
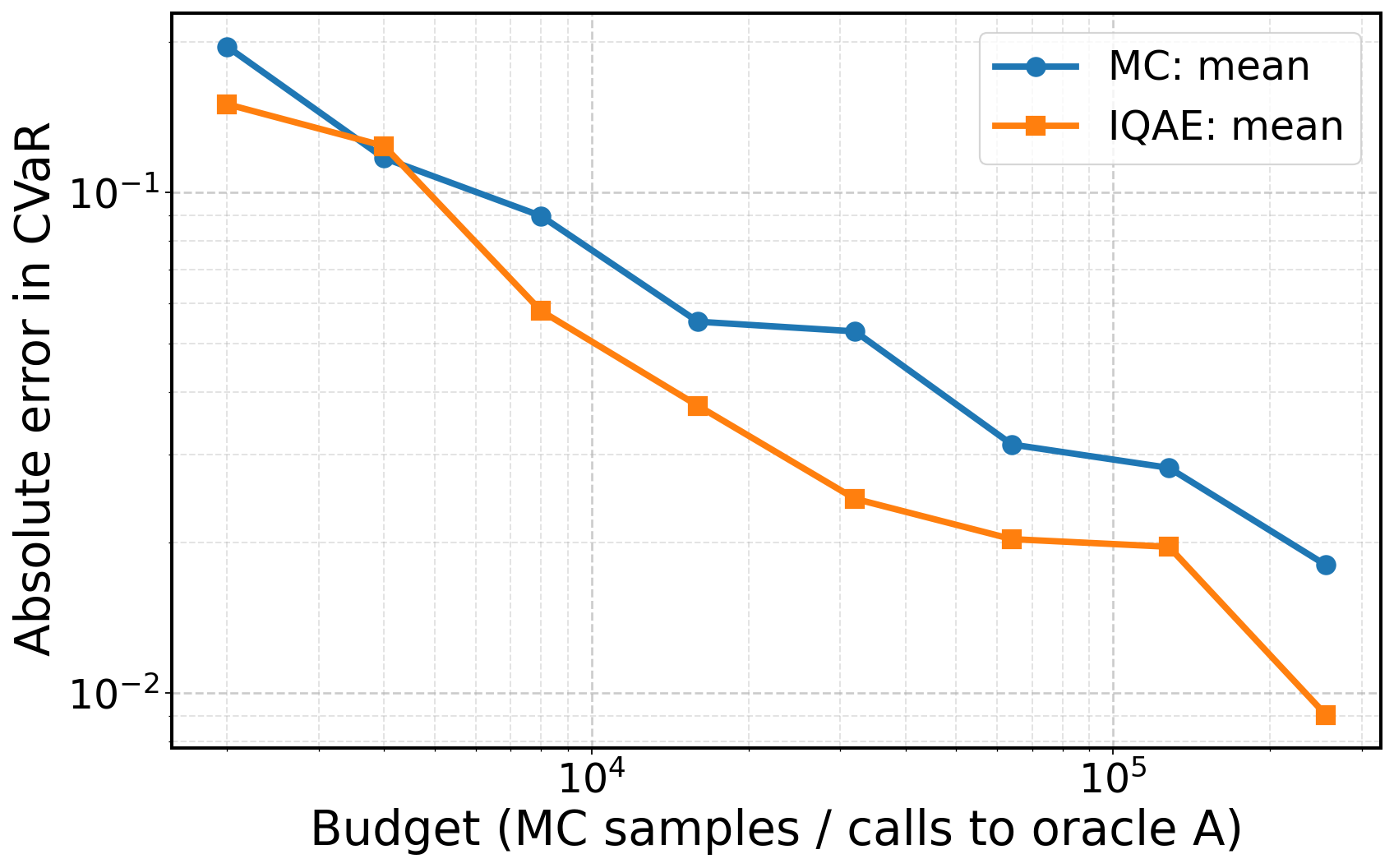
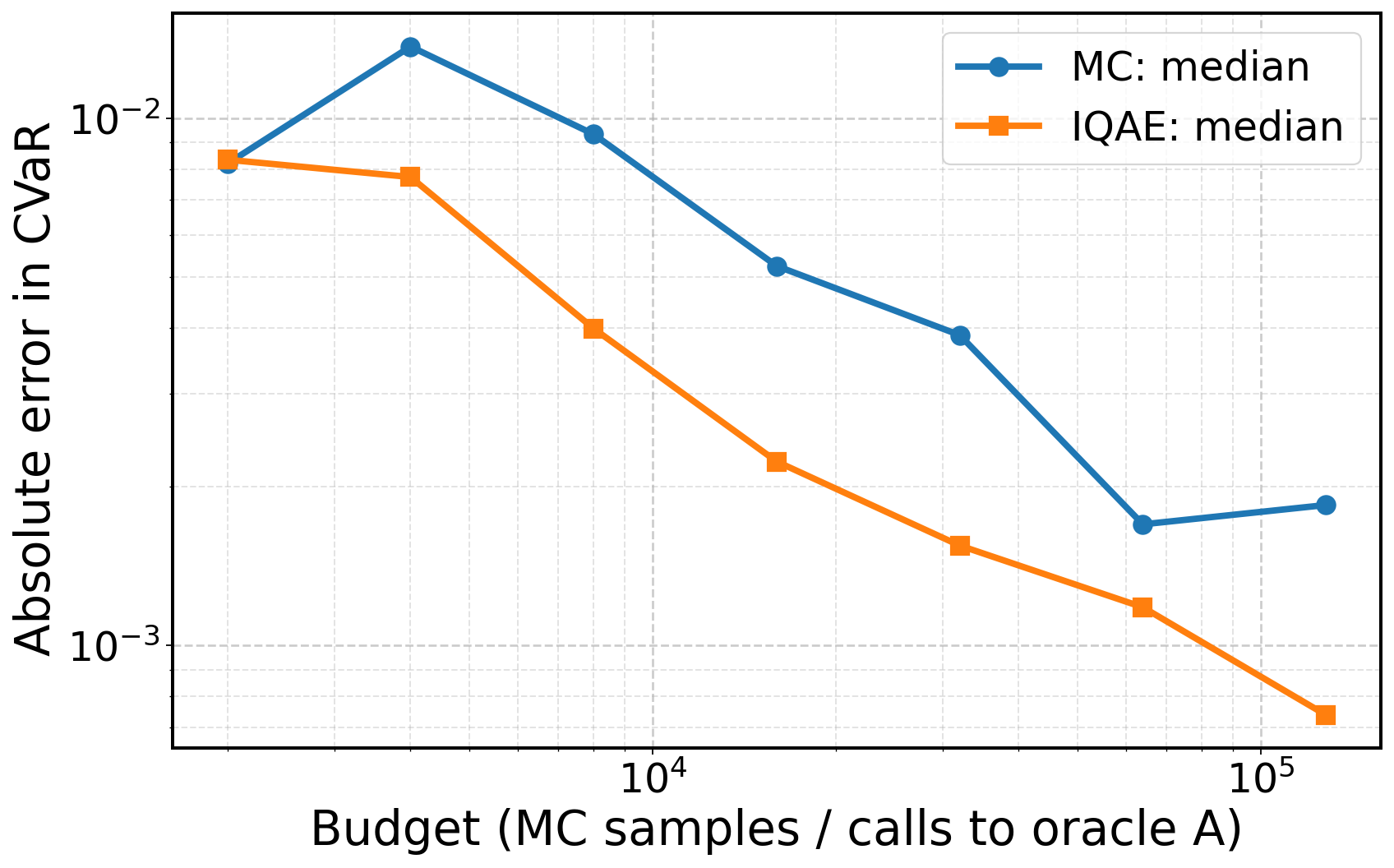
Iterative Quantum Amplitude Estimation (IQAE) demonstrates a quadratic speedup in sampling complexity relative to classical Monte Carlo methods for estimating Conditional Value at Risk (CVaR). This improvement stems from the algorithm’s utilization of quantum superposition and interference, allowing it to explore a solution space more efficiently. Benchmarking against classical methods consistently shows IQAE achieving lower error rates for a given number of samples, indicating a statistically significant performance advantage. Specifically, for an estimation error of ε, IQAE requires O(1/\epsilon) samples, whereas classical Monte Carlo requires O(1/\epsilon^2) samples, representing the quadratic speedup.
The core of the Iterative Quantum Amplitude Estimation (IQAE) algorithm lies in its translation of the Conditional Value at Risk (CVaR) estimation problem into a quantum oracle. This oracle, a black box function, defines a quantum state where the amplitude of a specific state encodes the probability of exceeding a given loss threshold. Grover Iteration, a quantum search algorithm, is then applied to this state, selectively amplifying the amplitude of states corresponding to outcomes exceeding the target CVaR level. This amplitude amplification process, repeated iteratively, increases the probability of measuring a state that accurately reflects the desired CVaR value, thereby enabling efficient estimation with a reduced number of quantum queries compared to classical methods. The efficiency of this process is directly linked to the structure of the oracle and the number of Grover iterations performed.
Modeling the Unseen: Gaussian Processes and Low-Rank Approximations
A Gaussian Process (GP) is employed as a prior distribution to model the inherent correlation structure within spatially correlated random fields. This approach defines a probability distribution over functions, allowing for the quantification of uncertainty in predictions. Specifically, the GP assumes any finite set of points follows a multivariate Gaussian distribution, fully characterized by a mean function and a covariance function k(x, x'). The covariance function defines the correlation between function values at different locations x and x', effectively encoding assumptions about the smoothness and shape of the underlying field. Utilizing a GP provides a complete probabilistic framework, yielding not only a prediction but also a predictive variance, which represents the uncertainty associated with that prediction.
The computational expense of Gaussian Process (GP) regression scales cubically with the number of data points, primarily due to the inversion of the covariance matrix. To mitigate this, we utilize the Nystrom method, a low-rank approximation technique. This involves selecting a subset of data points, termed inducing points, to construct a reduced-dimensionality representation of the covariance matrix. Specifically, the full n \times n covariance matrix is approximated by a m \times m inducing matrix, where m << n. This dimensionality reduction allows for efficient computation of the inverse and subsequent sampling from the GP posterior, significantly decreasing the computational cost while retaining a reasonable approximation of the original covariance structure.
The integration of Gaussian Processes with Low-Rank Nystrom approximations addresses a key limitation in applying the Implicit Quantization Algorithm for Exploration (IQAE) to high-dimensional problems. While IQAE theoretically offers a speedup over traditional Monte Carlo methods, its practical implementation is often hindered by the computational cost of covariance matrix operations. By representing the Gaussian Process covariance matrix in a low-rank form, the computational complexity is significantly reduced, allowing IQAE to scale effectively to higher dimensions. This results in improved sample efficiency – achieving comparable or superior results with fewer samples – when compared to standard Monte Carlo exploration strategies in spatially correlated random fields.
Beyond Prediction: Hypothesis Management and Interval Inference
The IQAE algorithm distinguishes itself through a sophisticated Hypothesis Management strategy, actively maintaining a dynamic set of plausible parameter values throughout the estimation process. Rather than converging on a single, potentially inaccurate, solution, the algorithm operates on a population of hypotheses, each representing a possible configuration of the underlying parameters. These hypotheses are not static; they are continuously refined through a series of quantum measurements. Each measurement acts as a selective pressure, favoring hypotheses that align with the observed data and suppressing those that deviate. This iterative refinement, guided by quantum principles, allows the algorithm to explore the parameter space more efficiently and robustly than classical methods, ultimately leading to a more accurate and reliable estimation of the Conditional Value at Risk CVaR.
The IQAE algorithm doesn’t simply iterate towards a solution; it actively prunes away unproductive lines of inquiry. A dedicated disambiguation step systematically eliminates spurious hypotheses-parameter value sets that, upon closer examination via quantum measurement, prove inconsistent with the observed data. This isn’t random discarding, but a focused reduction of the search space, concentrating computational effort on the most plausible regions of the parameter space. By intelligently discarding unlikely candidates, the algorithm achieves a more efficient and accurate estimation of Conditional Value at Risk (CVaR), avoiding the pitfalls of exploring irrelevant solutions and ultimately leading to a significantly reduced standard deviation in the CVaR error compared to traditional Monte Carlo methods.
The culmination of this quantum-enhanced estimation process lies in interval-based inference, which doesn’t simply yield a single CVaR value, but rather a confidence interval around that estimate-a crucial step for robust risk assessment. Through rigorous testing, notably with the L-bracket example, the algorithm achieves a remarkable 0.998 success probability, indicating a high degree of confidence in the estimated range. Importantly, this method consistently exhibits a lower standard deviation of CVaR error when contrasted with traditional Monte Carlo simulations, suggesting a more precise and reliable determination of potential financial risk. This precision is not merely academic; it allows for more informed decision-making by providing a quantifiable measure of uncertainty surrounding the estimated CVaR, moving beyond point estimates to a more comprehensive understanding of possible outcomes.
The pursuit of stabilized maximum-likelihood iterative quantum amplitude estimation, as detailed in this work, feels remarkably akin to grasping at shadows. Every refinement of the algorithm, every attempt to more accurately quantify conditional value-at-risk, is ultimately an approximation-a temporary bulwark against the inherent uncertainty of complex systems. As Epicurus observed, “It is impossible to live pleasurefully without living prudently, honorably, and justly.” This holds true for computational methods as well; seeking precision without acknowledging the limitations of the model is a delusion. The algorithm may improve the estimation of tail risk, but it does not eliminate the fundamental unknowability that underlies all attempts to model reality. Each calculation is an attempt to hold light in hands, and it slips away.
Beyond the Horizon
The presented methodology, while demonstrating a marked improvement in the efficiency of tail risk quantification, ultimately confronts the inherent limitations of any predictive model. Stabilized maximum-likelihood iterative quantum amplitude estimation, however elegant, offers merely a local approximation of a fundamentally chaotic system. Gravitational collapse forms event horizons with well-defined curvature metrics; similarly, any computational technique, even one leveraging quantum phenomena, encounters an informational horizon beyond which accuracy diminishes and uncertainty dominates. The pursuit of ever-finer resolution in uncertainty quantification is not necessarily a path toward truth, but a refinement of the illusion of control.
Future research must address not solely the algorithmic enhancement of CVaR estimation, but the very definition of ‘risk’ within complex systems. The fidelity of finite element analysis, the precision of quantum computation – these are all secondary to the underlying assumption that a system’s behavior can be adequately represented by a mathematical model. Singularity is not a physical object in the conventional sense; it marks the limit of classical theory applicability. Consequently, investigations into non-parametric methods and alternative frameworks that acknowledge the inherent unknowability of extreme events are crucial.
The ultimate challenge lies not in predicting the unpredictable, but in designing systems resilient to unforeseen consequences. The field may well advance beyond the quantification of tail risk to the development of adaptive structures capable of accommodating, rather than resisting, the inevitable disruptions that lie beyond the computational event horizon.
Original article: https://arxiv.org/pdf/2602.09847.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Build Muscle in Half Sword
- YAPYAP Spell List
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- How to Unlock the Mines in Cookie Run: Kingdom
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
- Epic Pokemon Creations in Spore That Will Blow Your Mind!
- Gears of War: E-Day Returning Weapon Wish List
- How to Get Wild Anima in RuneScape: Dragonwilds
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
- Top 8 UFC 5 Perks Every Fighter Should Use
2026-02-12 00:49