Quantum Spin Control: Balancing Speed and Reliability

by

Author: Denis Avetisyan

A new variational algorithm optimizes state transfer in complex spin chains, revealing fundamental limits between performance and noise resilience.

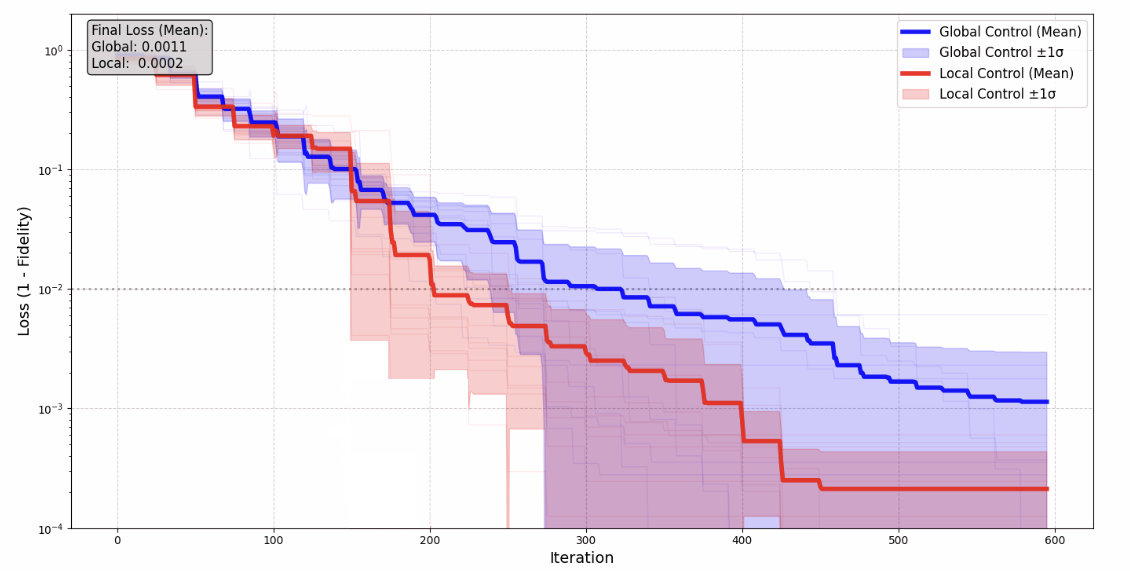
Optimization trajectories, assessed across ten realizations with parameters $N=3$, $T=2$, and $L=8$, demonstrate that local control converges more rapidly and achieves a significantly lower final loss—approximately $2 \times 10^{-4}$—compared to global control, which plateaus around $1.1 \times 10^{-3}$, highlighting the efficiency gains achieved through localized optimization strategies.
Optimization trajectories, assessed across ten realizations with parameters $N=3$, $T=2$, and $L=8$, demonstrate that local control converges more rapidly and achieves a significantly lower final loss—approximately $2 \times 10^{-4}$—compared to global control, which plateaus around $1.1 \times 10^{-3}$, highlighting the efficiency gains achieved through localized optimization strategies.

Researchers demonstrate a hybrid quantum-classical approach to achieving high-fidelity state transfer in spin chains, identifying a trade-off between control expressivity and robustness to noise.

Achieving high-fidelity quantum state transfer in extended systems remains a significant challenge due to the complexities of multi-qubit control. This is addressed in ‘Trotterized Variational Quantum Control for Spin-Chain State Transfer’, which introduces a hybrid variational algorithm for optimizing control pulses in spin chains. The study reveals that global parameterizations of control schemes offer improved robustness against depolarizing noise compared to local approaches, albeit with a trade-off in expressivity. Could this balance between control complexity and noise resilience pave the way for scalable quantum control synthesis on near-term quantum devices?

Breaking Coherence: The Challenge of Quantum State Control

Reliable quantum state transfer is fundamental to emerging quantum technologies, yet practical implementation suffers from sensitivity to environmental noise. Maintaining coherence during information transfer demands precise control and shielding, a task that intensifies with system size. Traditional control techniques rely on computationally intensive methods, like Pontryagin’s Maximum Principle, which become intractable for complex many-body systems. Theoretical models, such as the $XXZ$ Hamiltonian, add mathematical complexity, hindering effective control strategy design. Every exploit begins with questioning the system, not intending to break it.

Variational Algorithms: A New Paradigm for Quantum Control

Optimizing complex quantum dynamics, particularly in high-dimensional, noisy systems, presents significant challenges for traditional methods. ‘Variational Quantum Algorithms’ offer a promising alternative, combining classical optimization with quantum computation. These algorithms employ ‘Global Control Parameterization’ and ‘Local Control Parameterization’ to shape control fields. Global control utilizes a single parameter set, while local control divides the field into segments. Efficient optimization relies on algorithms like ‘SLSQP’ to maximize state transfer probability. Results demonstrate global control achieves approximately 0.989 fidelity, significantly exceeding local control.

During training with depolarizing noise at $p=10^{-3}$, global control rapidly achieves an accuracy of approximately 0.989, while local control saturates at around 0.452, as evidenced by the semi-log loss, with the shaded region emphasizing this performance disparity.
During training with depolarizing noise at $p=10^{-3}$, global control rapidly achieves an accuracy of approximately 0.989, while local control saturates at around 0.452, as evidenced by the semi-log loss, with the shaded region emphasizing this performance disparity.

Robustness Against the Noise: Fidelity in Quantum Systems

Mitigating ‘Depolarizing Noise’ – which degrades quantum information and reduces control fidelity – is crucial for practical quantum technologies. ‘Variational Quantum Algorithms’ effectively design noise-resilient control pulses, maximizing state transfer fidelity. Specifically, with $p=10^{-3}$ depolarizing noise, global control achieves 0.989 fidelity, significantly outperforming local control at 0.452. Approximation techniques like ‘Trotterization’ simplify complex dynamics, enabling efficient optimization and control of larger systems.

Harmonic Control: Sculpting Quantum Potential

Implementing ‘Harmonic Potential’ profiles creates spatially correlated control fields, enabling smoother, more reliable state transfer. This moves beyond traditional methods by shaping the potential landscape experienced by qubits, allowing precise manipulation and reduced error rates. This refined control demonstrably reduces sensitivity to imperfections, improving performance and stability. The study reports a 2.19x improvement in noise tolerance, quantified as the Robustness Ratio, for global control schemes. The convergence of variational algorithms, harmonic control, and robust optimization suggests a viable pathway toward scalable, fault-tolerant quantum technologies, hinting at the expansion of computational boundaries.

The pursuit of high-fidelity state transfer, as detailed in this work, inherently demands a dismantling of conventional approaches. The researchers effectively challenged established methods by introducing a hybrid variational quantum algorithm, probing the limits of expressivity versus robustness. This mirrors the sentiment of Paul Dirac, who once stated, “I have not the slightest idea of what I am doing.” Dirac’s quote isn’t an admission of incompetence, but a declaration of intellectual honesty – a willingness to venture into the unknown, to break down established frameworks to understand the underlying principles. The investigation into global versus local control schemes, and their differing responses to noise, exemplifies this spirit – a controlled demolition of assumptions in the name of deeper understanding.

Beyond the Chain

The demonstrated fidelity of state transfer, while notable, merely highlights the persistent friction between ideal quantum manipulation and the messy reality of decoherence. The trade-off identified – expressivity sacrificed for robustness – isn’t a limitation to be ‘solved’, but a fundamental characteristic to be exploited. Future investigations shouldn’t aim for perfect control, an asymptotic goal, but rather the deliberate engineering of controlled errors. What if noise, rather than being suppressed, becomes a resource for sculpting desired quantum states? This demands a shift in perspective—from seeking to eliminate imperfections, to learning to direct them.

The current work focuses on spin chains, a mathematically convenient system. However, the true test lies in extending these hybrid variational approaches to more complex, physically relevant architectures. Exploring control schemes for systems with long-range interactions, or those exhibiting non-Markovian dynamics, will inevitably expose the limits of current Trotterization techniques. The question then becomes not how to improve the approximation, but whether a fundamentally different approach to variational optimization is required—one that doesn’t rely on decomposing the Hamiltonian into manageable, albeit artificial, steps.

Ultimately, the success of quantum control hinges on recognizing that the universe isn’t obligated to conform to the elegance of theoretical models. The challenge isn’t to impose order on chaos, but to discover the hidden order within it. A truly robust quantum algorithm will not simply function despite noise, but will utilize it, transforming imperfection into a defining characteristic of the computation itself.

Original article: https://arxiv.org/pdf/2511.09684.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2025-11-15 07:48