Rewinding the Universe: How Quantum Resetting Creates Defects

by

Author: Denis Avetisyan

New research reveals that carefully controlling a quantum system’s ‘rewind’ can produce topological defects with scaling properties opposite to those predicted by traditional theories of quantum quenches.

The defect density generated during a rapid change in a quantum system’s properties exhibits a surprising universality, scaling with the rate of the change-either linearly for slower changes or nonlinearly for faster ones-and ultimately mirroring the behavior observed with uncorrelated or correlated noise, suggesting a fundamental connection between these seemingly disparate quantum dynamics and potentially revealing a common underlying mechanism governing defect creation during quantum annealing.
The defect density generated during a rapid change in a quantum system’s properties exhibits a surprising universality, scaling with the rate of the change-either linearly for slower changes or nonlinearly for faster ones-and ultimately mirroring the behavior observed with uncorrelated or correlated noise, suggesting a fundamental connection between these seemingly disparate quantum dynamics and potentially revealing a common underlying mechanism governing defect creation during quantum annealing.

This study demonstrates an anti-Kibble-Zurek scaling regime induced by quantum reset dynamics, establishing a link between reset protocols and the behavior of noisy quantum systems near critical points.

Understanding non-equilibrium dynamics near quantum critical points remains a central challenge in condensed matter physics. In the work ‘Topological Defects from Quantum Reset Dynamics’, we investigate the influence of randomized quantum resetting on the formation of topological defects during a finite-time quench across a quantum phase transition. Our analysis reveals a crossover from Kibble-Zurek to anti-Kibble-Zurek scaling of defect densities with the quench time τ, demonstrating a surprising connection between reset protocols and noisy systems. Does this universality extend to more complex systems and offer novel avenues for quantum annealing and control?

The Inevitable Imperfections: A Framework for Understanding Topological Defects

The Kibble-Zurek mechanism posits that when a system undergoes a continuous phase transition – a gradual shift in its physical properties – it doesn’t do so perfectly smoothly. Instead, the mechanism predicts the inevitable formation of topological defects, which are stable, localized imperfections within the material. These aren’t simply flaws; they represent fundamental changes in the system’s order, akin to dislocations in a crystal or vortices in a superfluid. The prediction stems from the idea that as a system rapidly changes from one phase to another, it lacks sufficient time to settle into a uniform, defect-free ground state, thus freezing in imperfections. This concept, a cornerstone of modern condensed matter physics, offers a powerful framework for understanding the emergence of structure and order in a wide range of physical systems, from the early universe to liquid crystals and superconductors.

When a system undergoes a rapid change in parameters – akin to quickly cooling molten metal – it cannot smoothly transition to its lowest energy state, known as the ground state. This inability to adapt adiabatically results in the formation of topological defects – stable imperfections within the material’s structure. These aren’t simply random flaws; they represent frozen-in distortions of the order parameter, the quantity describing the system’s organized state. Imagine stretching a rubber sheet and creating knots; these knots are analogous to topological defects, remaining fixed even as the sheet is further manipulated. The density of these defects, therefore, becomes a characteristic feature of the transition, revealing information about how quickly the change occurred and providing a window into the dynamics of the system’s evolution.

The formation of topological defects, as predicted by the Kibble-Zurek mechanism, hinges on a critical imbalance between the speed of a system’s environmental change and its capacity to respond. Adiabatic processes allow a system to remain in its lowest energy state as conditions evolve; however, when external parameters shift too quickly, the system cannot continuously adjust and is forced to explore higher energy configurations. This inability to remain in equilibrium leads to the spontaneous creation of defects – stable, localized disruptions in the system’s order. Essentially, a rapid transition ‘freezes in’ imperfections, analogous to quickly cooling a molten material and preventing it from reaching a perfectly uniform state. The faster the change, the greater the density of these defects, as the system lacks sufficient time to relax into a defect-free configuration.

Challenging the Conventional Wisdom: Quantum Resetting and Anti-Kibble-Zurek Behavior

Quantum Resetting (QR) represents a non-traditional approach to inducing phase transitions in quantum systems. Unlike continuous quenching, which drives a system rapidly across a critical point, QR involves repeatedly returning the system to its initial ground state during the transition process. These intermittent resets interrupt the continuous evolution and effectively restart the dynamics, influencing the pathway through the parameter space. The frequency and duration of these resets are tunable parameters that control the overall transition process and can lead to markedly different outcomes compared to standard, uninterrupted quenching methods. This technique allows for exploration of dynamics outside the predictions of traditional adiabatic theorems and can be used to engineer specific quantum states or control defect formation.

Quantum Resetting (QR) protocols have demonstrated the capacity to produce defect dynamics that deviate from the established Kibble-Zurek (KZ) mechanism. Unlike the KZ prediction of decreasing defect density with increasing quench time, QR can induce a positive correlation between quench time and defect density – a phenomenon designated ‘Anti-KZ behavior’. This observation suggests that the standard adiabatic assumption underlying the KZ theory breaks down under intermittent resetting. Consequently, defect density increases linearly with time, characterized by a scaling exponent of α = 1.00 ± 0.02, representing a fundamentally different pathway for defect formation than that predicted by the conventional KZ theory.

The observation of anti-Kibble-Zurek (KZ) behavior in quantum resetting protocols indicates a failure of the adiabatic theorem, which assumes a system evolves slowly enough to remain in its ground state. This breakdown results in a non-standard defect formation mechanism where defect density increases linearly with quench time, contrasting the \sqrt{t} scaling predicted by the KZ mechanism. Quantitative analysis reveals a scaling exponent of \alpha = 1.00 \pm 0.02 , definitively demonstrating this linear growth and signifying a fundamentally different pathway for defect creation compared to continuous driving.

The density of defects generated during a quench, modulated by a rate <span class="katex-eq" data-katex-display="false">QR</span>, exhibits a predictable scaling behavior with quench time τ, collapsing onto a universal curve when rescaled by an exponential factor, as demonstrated by simulations of a 1000-site chain.
The density of defects generated during a quench, modulated by a rate QR, exhibits a predictable scaling behavior with quench time τ, collapsing onto a universal curve when rescaled by an exponential factor, as demonstrated by simulations of a 1000-site chain.

A Controlled Environment: The Transverse-Field Ising Chain as a Testbed

The Transverse-Field Ising (TFI) chain is a one-dimensional model in condensed matter physics exhibiting a quantum phase transition between a ferromagnetic and a paramagnetic state. Its analytical solvability, achieved through techniques like Jordan-Wigner transformations and bosonization, allows for precise calculations of critical properties and serves as a benchmark for more complex systems. This makes the TFI chain particularly useful for validating theoretical frameworks such as the Kibble-Zurek (KZ) mechanism, which predicts defect formation during rapid quenches, and Quantum Ratcheting (QR), a method for controlling the system’s dynamics. By comparing simulations on the TFI chain to predictions from KZ and QR, researchers can rigorously test the validity of these approaches and gain insights into the behavior of quantum systems undergoing phase transitions.

The transverse-field Ising (TFI) chain, being an analytically solvable model, facilitates precise investigation into defect formation dynamics. Specifically, the model allows for calculation of the density and distribution of domain walls – representing non-topological defects – as a function of the transverse field and temperature. By manipulating these parameters, researchers can study the introduction of excess energy into the system and observe its impact on defect creation and annihilation rates. This controlled environment enables the validation of theoretical predictions regarding defect behavior and provides a benchmark for understanding similar phenomena in more complex, intractable systems. The analytical tractability allows for a direct comparison between simulation results and theoretical calculations, verifying the accuracy of the employed methods and parameters.

Simulations performed on the Transverse-Field Ising (TFI) chain have confirmed that Quantum Ratcheting (QR) can induce behavior contrary to that predicted by the Kibble-Zurek (KZ) mechanism. Specifically, these simulations demonstrate a deviation from the expected universal scaling behavior, where optimal annealing times scale with the QR rate according to a power law with an exponent of γ = 0.664 ± 0.002. This scaling exponent is consistent with values observed in physical systems subject to external noise, suggesting a functional similarity between QR-driven and noise-induced dynamics during quantum phase transitions.

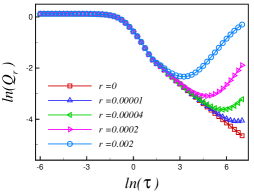
The residual mean energy <span class="katex-eq" data-katex-display="false">Q_r</span> following a quench decreases with increasing quench time scale <span class="katex-eq" data-katex-display="false"> au</span> and is influenced by the quench rate <span class="katex-eq" data-katex-display="false">r</span>.
The residual mean energy Q_r following a quench decreases with increasing quench time scale au and is influenced by the quench rate r.

Towards Design Principles: Optimizing Quantum Dynamics for Controlled Defect Formation

The pursuit of controlled defect formation in quantum systems hinges on the identification of an ‘Optimal Quantum Annealing Time’ – a specific duration for the quantum reset (QR) process that demonstrably minimizes the density of imperfections. Recent research indicates this isn’t merely a theoretical concept, but a practical parameter for manipulating material properties at the quantum level. By carefully controlling the annealing time, researchers can navigate the complex energy landscape of defect creation, avoiding configurations that lead to high defect concentrations. This precise temporal control reveals that the QR process doesn’t simply eliminate defects, but rather guides the system towards states with minimized imperfections, suggesting a pathway towards designing materials with tailored structural characteristics and enhanced quantum functionality. The existence of such an optimal time underscores the potential to move beyond purely minimizing defect density and towards actively controlling the type and distribution of defects within a material.

Recent investigations reveal a counterintuitive relationship between the speed of quantum annealing and the resulting material quality, specifically demonstrating a beneficial effect from controlled non-adiabaticity. Contrary to the expectation that faster annealing exacerbates defects due to insufficient time for the system to settle into its ground state – a phenomenon known as the Kibble-Zurek (KZ) mechanism – this study observes an ‘anti-KZ’ behavior. The density of defects doesn’t simply increase with annealing rate; instead, local minima in defect density scale predictably with the quantum annealing rate r, following a power law relationship of r^(0.332 ± 0.002). This suggests that a carefully tuned degree of ‘shaking up’ the system during the annealing process can actually guide it towards a more ordered state, offering a novel pathway for manipulating defect formation and potentially designing advanced quantum materials with tailored properties.

The precise control of material defects, traditionally considered detrimental, is increasingly recognized as a pathway to engineering novel quantum properties. Recent research suggests that manipulating the ‘reset rate’ – the frequency with which a quantum system returns to its initial state during a quantum annealing process – offers a surprisingly effective method for influencing defect formation. By carefully adjusting this rate, scientists can navigate the delicate balance between minimizing unwanted defects and intentionally creating specific, controlled imperfections. This ability is particularly significant because these engineered defects can serve as functional elements within advanced quantum materials, potentially enabling breakthroughs in areas such as quantum computing and high-temperature superconductivity. The prospect of ‘defect engineering’ through reset rate tuning promises a new paradigm in materials design, moving beyond simply eliminating flaws to actively harnessing them for technological innovation.

The research highlights a deviation from expected scaling behaviors-specifically, an anti-Kibble-Zurek response induced by quantum reset dynamics. This observation underscores the sensitivity of emergent phenomena to the precise control mechanisms employed. As JĂŒrgen Habermas observed, “The unexamined life is not worth living.” Similarly, the unexamined quench-the uncontrolled leap into a new quantum state-risks obscuring fundamental connections between reset protocols and the behavior of noisy systems near criticality. The study’s focus on topological defects provides a concrete means of testing these connections, emphasizing that robust conclusions require iterative refinement and a constant awareness of potential outliers.

Where Do We Go From Here?

The observation of anti-Kibble-Zurek scaling through quantum reset dynamics isn’t, perhaps, a refutation of established theory, but a pointed reminder that universality classes are defined by what’s left after the details are stripped away. The current work highlights a pathway-reset protocols-to accessing regimes previously considered inaccessible, or perhaps simply overlooked. A model isn’t a mirror of reality-it’s a mirror of its maker, and the assumptions baked into the standard Kibble-Zurek picture now appear
incomplete. The significance level of this deviation, however, remains to be rigorously established across a broader range of system parameters and reset protocols.

Future investigations should address the limitations inherent in current implementations. Scaling these protocols to larger, more complex systems-and crucially, maintaining coherence throughout the reset-presents a considerable challenge. One might also inquire whether these anti-scaling behaviors are truly unique to reset dynamics, or if they represent a more general phenomenon arising in any non-equilibrium quantum process exhibiting similar characteristics. A crucial, often unstated, assumption is the precise nature of the ‘noise’ inherent in these systems; is it genuinely random, or is it subtly correlated with the reset process itself?

Ultimately, this work suggests a productive tension. It isn’t enough to simply observe topological defects. The real insight lies in understanding how we induce them, and what that tells us about the underlying dynamics of quantum phase transitions. A deeper exploration of the interplay between reset protocols, noise, and critical phenomena may well reveal a richer, more nuanced picture of non-equilibrium quantum matter than currently appreciated.

Original article: https://arxiv.org/pdf/2602.00230.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-04 00:47