Rewriting Hadronization: A Diffusion-Based Approach

Author: Denis Avetisyan

A new framework recasts the complex process of hadronization as a conditioned stochastic diffusion, offering a consistent path toward both theoretical understanding and improved simulations.

String hadronization is modeled through complementary frameworks-one depicting string breaks within a light-cone coordinate system where the probability is governed by worldsheet area, and another representing hadronization as a discrete Markov chain evolving remaining string mass <span class="katex-eq" data-katex-display="false">M_n \to M_{n+1}</span> until termination occurs either within the band <span class="katex-eq" data-katex-display="false">\mathcal{S}=[M\_{\star},M\_{\rm cut}][latex] or by undershooting into [latex]\mathcal{F}=(0,M\_{\star})</span>. — String hadronization is modeled through complementary frameworks-one depicting string breaks within a light-cone coordinate system where the probability is governed by worldsheet area, and another representing hadronization as a discrete Markov chain evolving remaining string mass $M_n \to M_{n+1}$ until termination occurs either within the band $\mathcal{S}=[M\_{\star},M\_{\rm cut}][latex] or by undershooting into [latex]\mathcal{F}=(0,M\_{\star})$ .

This review demonstrates how the Doob transform can reconcile local Markovian dynamics with global conservation laws in effective hadronization models.

The seemingly local dynamics of hadronization are challenged by the need to satisfy global conservation laws, creating a tension within conventional models. This paper, 'Conservation laws and effective hadronization models', resolves this by recasting hadronization as a conditioned stochastic diffusion process, revealing how constraints induce correlations absorbed through a Doob h-transform. This formalism establishes a systematic framework-a tower of effective theories-exhibiting Wilsonian renormalization group structure and cleanly separating universal fragmentation dynamics from infrared effects. Could this approach not only refine theoretical predictions but also inspire novel, more accurate simulations of strong interaction processes?

Unveiling the Hidden Correlations in Hadronization

The prevailing understanding of hadronization - the process by which quarks and gluons transform into observable particles - often begins with a simplification: string fragmentation is treated as a local, Markovian process. This means each step in the string breaking is considered independent of all prior history, relying only on immediate conditions. This approach elegantly models the complex dynamics of Quantum Chromodynamics (QCD) by assuming that the decay at one point on the string doesn’t influence decay elsewhere. While computationally efficient and broadly successful in reproducing many experimental features, this local picture inherently sidesteps the full scope of QCD, allowing for a tractable, though ultimately incomplete, description of particle production. It offers a valuable starting point, but neglects the crucial, long-range correlations dictated by fundamental conservation laws.

The conventional understanding of how quarks bind into hadrons assumes a localized fragmentation process, where each breaking of the color string occurs independently of distant events. However, this picture clashes with fundamental physical laws; energy-momentum conservation and the requirement that hadrons possess a minimum mass introduce long-range correlations. These global constraints dictate that the fragmentation cannot be entirely local, as the creation of a hadron at one point on the string inevitably influences the possibilities for hadronization elsewhere. Consequently, the process becomes non-Markovian - the future state of the fragmentation is dependent not only on the present, but also on the entire history of string breaking - demanding a more holistic approach to accurately model the complex dynamics of hadron formation and resolve discrepancies in existing simulations.

The inherent conflict between local string fragmentation models and global conservation laws presents a significant obstacle to precisely charting the evolution of quark-gluon plasma into observable hadrons. Established frameworks, such as the LundStringModel, operate under the assumption of Markovian dynamics - where future hadronization steps depend only on the immediate present - yet fail to fully account for the long-range correlations imposed by energy-momentum conservation and minimum mass criteria. This discrepancy introduces systematic uncertainties in simulations, limiting the predictive capability of these models, particularly when attempting to accurately reproduce experimental data concerning particle multiplicities, momentum spectra, and azimuthal correlations. Consequently, refining hadronization models demands addressing this fundamental tension to achieve a more complete and reliable description of strong interaction processes.

A comprehensive understanding of hadron formation necessitates reconciling the apparent conflict between local string fragmentation models and the fundamental global constraints of energy-momentum conservation and minimum mass requirements. Current models, while successful in many regimes, operate under a Markovian assumption - that a string breaks locally without ‘memory’ of its overall configuration - which clashes with the undeniable influence of these global principles. Resolving this tension isn’t merely a matter of refining existing parameters; it demands a fundamental shift towards non-Markovian descriptions capable of capturing the long-range correlations inherent in the process. Such a breakthrough promises not only more accurate simulations of particle collisions, but also a deeper insight into the underlying dynamics of Quantum Chromodynamics and the very nature of how quarks and gluons coalesce into the observable hadrons that constitute much of the visible universe.

The continuum limit of string mass evolution is governed by a drift coefficient <span class="katex-eq" data-katex-display="false">\mu(M)</span> with a UV fixed point at <span class="katex-eq" data-katex-display="false">\mu_{UV} \approx -0.23M</span> and a diffusion coefficient <span class="katex-eq" data-katex-display="false">\sigma^2(M)</span> scaling as <span class="katex-eq" data-katex-display="false">\sigma_{UV}^2 \propto M^2</span>, demonstrating scale-invariant UV behavior confirmed by insets approaching unity for <span class="katex-eq" data-katex-display="false">M \gtrsim 10</span> GeV, and is further characterized by an effective field theory tower with distinct infrared, running, and ultraviolet regimes. — The continuum limit of string mass evolution is governed by a drift coefficient $\mu(M)$ with a UV fixed point at $\mu_{UV} \approx -0.23M$ and a diffusion coefficient $\sigma^2(M)$ scaling as $\sigma_{UV}^2 \propto M^2$ , demonstrating scale-invariant UV behavior confirmed by insets approaching unity for $M \gtrsim 10$ GeV, and is further characterized by an effective field theory tower with distinct infrared, running, and ultraviolet regimes.

Restoring Consistency: The DoobHH Transformation

The DoobHH transform is a mathematical technique used to address renormalization within the fragmentation process. Specifically, it enables the extension of the $\text{BareFragmentationKernel}$ beyond its initial domain of definition by introducing a constraint-satisfying modification. This transform operates by conditioning the fragmentation probabilities on the adherence to predefined global constraints, effectively reweighting the possible fragmentation outcomes. The resulting renormalized kernel ensures that the overall fragmentation process remains physically plausible and respects established conservation laws, such as total mass or energy. This approach allows for calculations involving potentially divergent or ill-defined kernels by systematically incorporating the effects of these constraints into the fragmentation dynamics.

The DoobHH transform, when applied to string fragmentation, introduces an EmergentForce as a direct consequence of conditioning the process on global constraints - specifically, that total string mass remains conserved. This force manifests as a bias in the evolution of string mass, altering the probabilities associated with different fragmentation outcomes. Rather than a physically motivated force, it is a mathematical artifact of the renormalization procedure; enforcing these constraints necessitates modifying the underlying probabilities to ensure a valid, normalized distribution. The magnitude and direction of this EmergentForce are determined by the specific constraints imposed and the current state of the fragmentation process, effectively steering the mass evolution towards permissible configurations and preventing violations of the predefined global conservation laws.

The DoobHH transform incorporates the effects of conditioning on the fragmentation process through the framework of an Effective Field Theory (EFT). Specifically, the $EffectiveFieldTheoryTower$ represents an infinite series of terms, ordered by the number of interactions introduced by the conditioning procedure. Each term in this tower corresponds to an increasingly complex interaction that accounts for the bias induced by enforcing global constraints. By systematically including these terms, the EFT approach provides a controlled approximation, allowing for the calculation of observables to a desired level of accuracy. This parallels the standard EFT methodology of building an effective Lagrangian with an infinite number of derivative terms, where higher-order terms are suppressed by the energy scale.

The RenormalizedGenerator, derived from the DoobHH transform, preserves the Markovian property, meaning that future states depend only on the current state and not on the past history of the fragmentation process. This simplification is crucial for computational efficiency, as it allows for the use of iterative algorithms and avoids the need to track the full evolution of the string breakup. Maintaining a Markovian description does not introduce inaccuracies because the conditioning inherent in the DoobHH transform is systematically incorporated through the $\text{EffectiveFieldTheoryTower}$ , ensuring that all relevant physical effects are accounted for within the renormalized framework. Consequently, calculations can be performed with reduced complexity while retaining a high degree of predictive power regarding string hadronization.

The Doobhh-transformed fragmentation kernel <span class="katex-eq" data-katex-display="false">K_h(M \to M^{\prime}) = K_{\rm bare}(M \to M^{\prime}) \cdot h(M^{\prime})/h(M)</span> effectively suppresses unsafe transitions near <span class="katex-eq" data-katex-display="false">M_{\rm cut} = 1.0</span> GeV while retaining the bare kernel's behavior at large masses where the conditioning effect diminishes. — The Doobhh-transformed fragmentation kernel $K_h(M \to M^{\prime}) = K_{\rm bare}(M \to M^{\prime}) \cdot h(M^{\prime})/h(M)$ effectively suppresses unsafe transitions near $M_{\rm cut} = 1.0$ GeV while retaining the bare kernel's behavior at large masses where the conditioning effect diminishes.

Quantifying Predictive Power: The Success Probability

The SuccessProbability, denoted as $P_{succ}$ , functions as a renormalization factor in the hadronization process, directly addressing the discrepancy between theoretical calculations and experimental data. This probability quantifies the likelihood that a given theoretical prediction will accurately reflect observed particle distributions. By renormalizing the theoretical output with $P_{succ}$ , the model effectively accounts for contributions from higher-order terms and non-perturbative effects not explicitly included in the initial calculation. This renormalization procedure is essential for achieving quantitative agreement between theory and experiment, allowing for precise extraction of parameters and validation of the underlying effective field theory. The accurate determination of $P_{succ}$ is therefore a critical component in bridging the gap between theoretical predictions and empirical observations in high-energy physics.

The calculation of SuccessProbability relies on incorporating the contribution of TailOperators, which represent non-perturbative effects manifesting as rare, order-one fluctuations in string mass. These operators are essential for completing the renormalization process because they account for contributions that are not suppressed by the large number of color degrees of freedom. Without accurately modeling these TailOperators, the renormalization procedure remains incomplete, leading to inaccuracies in matching theoretical predictions to experimental observables. The contribution from TailOperators is not analytically solvable and therefore requires dedicated numerical evaluation within the framework of the stochastic hadronization model.

The SuccessProbability is directly linked to the Effective Field Theory (EFT) Tower, facilitating systematic improvements to calculations and providing a means for rigorous uncertainty quantification. Specifically, the EFT Tower represents an expansion in powers of $\Lambda_{QCD}^{-1}$ , where each term corresponds to a higher-order correction. The SuccessProbability allows for the consistent inclusion of these higher-order terms, enabling a controlled approximation of the full quantum chromodynamics (QCD) result. By tracking the contribution of each term in the EFT Tower to the SuccessProbability, researchers can estimate the theoretical uncertainty associated with truncating the expansion, providing a quantifiable measure of the approximation’s reliability and guiding the inclusion of further refinements.

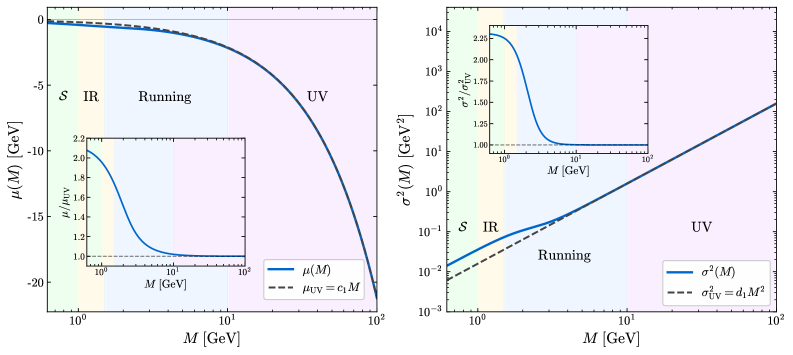
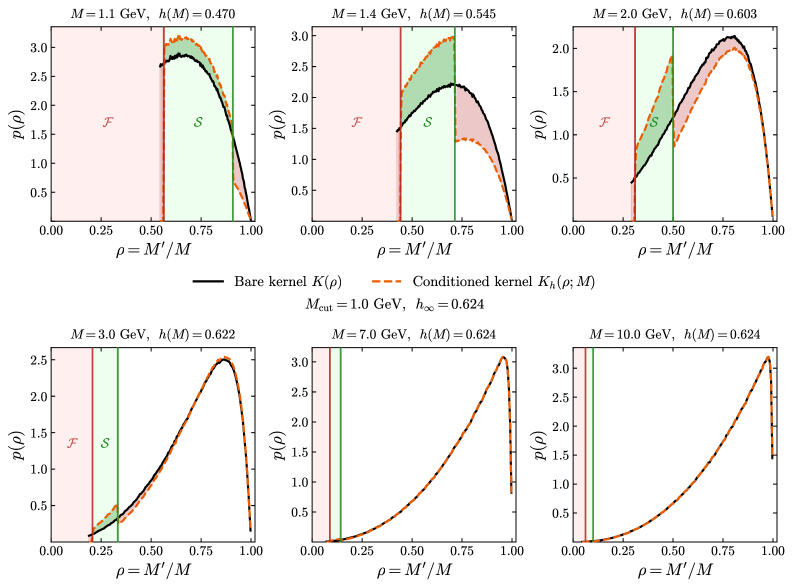
This research establishes hadronization as a conditioned stochastic process, enabling quantitative comparison with established theoretical models. Validation through Monte Carlo simulations demonstrates approximately 8% accuracy within the boundary layer - the region of transition in the simulation - and achieves 2-3% accuracy in the asymptotic regime, where the simulation reaches a stable, predictable state. These results confirm the effectiveness of the implemented framework for modeling hadronization and provide a measurable level of precision for validating the underlying effective field theory.

Non-local tail operators encode single-step transition probabilities, with the failure operator <span class="katex-eq" data-katex-display="false">\Gamma_{\mathcal{F}}(M)</span> representing the probability of undershooting to <span class="katex-eq" data-katex-display="false">\mathcal{F}=(0,M_{\star})</span> and the termination operator <span class="katex-eq" data-katex-display="false">\Gamma_{\mathcal{S}}(M)</span> representing the probability of landing in <span class="katex-eq" data-katex-display="false">\mathcal{S}=[M_{\star},M_{\rm cut}]</span>, both scaling as <span class="katex-eq" data-katex-display="false">(M_{\rm scale}/M)^{2(a+1)} \approx (M_{\rm scale}/M)^{3.4}</span> in the ultraviolet regime and becoming order one near <span class="katex-eq" data-katex-display="false">M_{\rm cut}</span>. — Non-local tail operators encode single-step transition probabilities, with the failure operator $\Gamma_{\mathcal{F}}(M)$ representing the probability of undershooting to $\mathcal{F}=(0,M_{\star})$ and the termination operator $\Gamma_{\mathcal{S}}(M)$ representing the probability of landing in $\mathcal{S}=[M_{\star},M_{\rm cut}]$ , both scaling as $(M_{\rm scale}/M)^{2(a+1)} \approx (M_{\rm scale}/M)^{3.4}$ in the ultraviolet regime and becoming order one near $M_{\rm cut}$ .

The presented work elegantly addresses the challenge of maintaining global conservation laws within a fundamentally local, stochastic process-a problem echoed throughout various scientific disciplines. This approach, framing hadronization as a conditioned diffusion, finds resonance with the Stoic philosophy of accepting what one cannot control while focusing on internal consistency. As Marcus Aurelius observed, “Very little is needed to make a happy life; it is all that you make it.” Similarly, this research doesn’t attempt to eliminate the stochasticity inherent in hadronization, but rather conditions it-shapes it-to align with established physical constraints. The Doob transform serves as the tool to impose this order, allowing for a theoretically sound and practically applicable model. If a pattern cannot be reproduced or explained, it doesn’t exist.

Beyond the Fragmentation

The reframing of hadronization as a conditioned stochastic diffusion, while offering a compelling resolution to the tension between locality and global conservation, inevitably reveals new contours to the unknown. The Doob transform, a powerful tool in this context, demands further investigation into its practical implementation and potential limitations when confronted with the full complexity of strong interaction dynamics. Errors, naturally, will be critical; every deviation from predicted behavior presents not a failure of the model, but an opportunity to uncover hidden dependencies within the fragmentation process.

A pressing challenge lies in extending this framework beyond the idealized scenarios typically employed in effective field theory. Real QCD is messy, and the constraints imposed by global conservation laws may not be as cleanly separated from the local diffusion as the current formalism suggests. The interplay between different conserved quantities-baryon number, charge, strangeness-deserves particular attention; their correlations, often treated as secondary effects, could reveal fundamental aspects of the underlying dynamics.

Ultimately, the true test will reside in the predictive power of this approach. Can the framework generate novel insights into hadron spectra, angular distributions, and, crucially, the long-standing puzzle of hadronization at future colliders? The path forward is not merely about refining existing simulations, but about embracing the unexpected-for within those anomalies lies the potential for a deeper understanding of the strong force.

Original article: https://arxiv.org/pdf/2602.12599.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

Unveiling the Hidden Correlations in Hadronization

Restoring Consistency: The DoobHH Transformation

Quantifying Predictive Power: The Success Probability

Beyond the Fragmentation

See also: