Author: Denis Avetisyan
New research reveals that interconnected superfluid rings can sustain persistent currents through a collective synchronization effect, offering insights into the behavior of complex quantum systems.
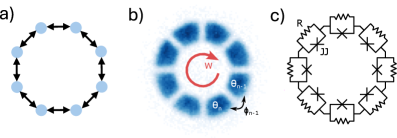
Cooperative effects in annular superfluid networks with Josephson junctions are accurately described by a Kuramoto-like model, demonstrating topological stabilization of phase coherence.
Maintaining stable collective behavior in coupled systems remains a fundamental challenge across diverse physical platforms. In the work ‘Cooperative stabilization of persistent currents in superfluid ring networks’, we demonstrate that persistent currents in annular superfluids with Josephson junctions are stabilized by a cooperative effect intrinsically linked to the ring topology. This stabilization arises from a collective synchronization phenomenon accurately described by a network of Kuramoto-like oscillators, offering robustness to noise and imperfections. Could this topological stability principle be generalized to other coupled oscillator networks, paving the way for enhanced control and coherence in complex systems?
The Illusion of Complexity: Unveiling Order from Oscillation
Conventional methodologies for simulating complex systems frequently encounter limitations when attempting to replicate emergent behavior – phenomena arising from interactions rather than inherent properties of individual components. This challenge is particularly acute in strongly interacting networks, where numerous feedback loops and nonlinear dynamics obscure simple cause-and-effect relationships. Traditional computational models, often reliant on averaging or simplification, can inadvertently wash out these crucial interactions, leading to inaccurate predictions or a failure to capture the system’s true complexity. The difficulty stems from the sheer number of variables and the intricate ways they influence one another; accurately representing these interactions demands computational resources that quickly become prohibitive as network size and connectivity increase. Consequently, a need exists for innovative platforms capable of faithfully reproducing these intricate dynamics and providing a more nuanced understanding of collective behavior.
A groundbreaking platform for studying collective behavior has been realized through the construction of a superfluid ring network. This innovative system utilizes the quantized vortices within a superfluid-acting as coupled oscillators-to model complex interactions found in diverse physical, biological, and social networks. By precisely controlling the interactions between these vortices as they circulate within the ring, researchers can investigate the emergence of synchronization and collective dynamics-phenomena where individual elements spontaneously coordinate their behavior. Unlike traditional computational models, this physical system allows for direct observation of these processes, providing unique insights into how global order arises from local interactions and offering a novel approach to understanding strongly coupled systems where emergent behaviors are often difficult to predict.
The superfluid ring network presents a compelling means to study how individual components within a complex system give rise to large-scale, coordinated behavior. Unlike traditional computational models that often rely on abstract representations, this platform utilizes the intrinsic, physical coupling of oscillating elements, allowing researchers to directly observe the emergence of global order from local interactions. This approach bypasses the limitations of simulating interactions, instead realizing them, and provides a fertile ground for investigating phenomena such as synchronization, pattern formation, and collective decision-making. Consequently, insights gained from this system extend beyond the confines of physics, offering potentially transformative understandings in fields like neuroscience, social dynamics, and even economic modeling, where identifying the link between individual agency and system-level outcomes remains a central challenge.
Imprinting Order: Control and Modeling of Collective States
Phase imprinting allows for the controlled establishment of the initial phase distribution of the condensate wavefunction around the superfluid ring. This is accomplished by momentarily applying a magnetic field pulse that shifts the phase of the condensate by 2\pi at a localized point, effectively introducing a defined phase singularity. The magnitude of this induced phase shift is directly proportional to the integer winding number, n, which characterizes the topological properties of the superfluid flow. By precisely controlling the duration and amplitude of the magnetic pulse, researchers can reliably set the initial winding number of the ring, facilitating investigations into the dynamics of quantized vortices and their relationship to persistent currents.
The complex dynamics of the superfluid network are modeled using an equivalent Resistively and Capacitively Shunted Junction (RSJ) circuit representation. This approach maps the superfluid flow to circuit elements – inductance representing kinetic energy, capacitance representing stored energy, and resistance accounting for dissipation. By characterizing the superfluid network with parameters such as critical current I_c, capacitance C, and resistance R, we can utilize well-established circuit analysis techniques to predict and interpret the observed behavior, effectively reducing the dimensionality of the problem and facilitating theoretical comparisons with experimental results. This simplification is crucial for understanding the stability and dynamics of various superfluid states.
Combining phase imprinting for experimental control with an equivalent RSJ circuit model enables systematic investigation of superfluid network stability. By varying imprinted phases and analyzing corresponding circuit parameters-capacitance, resistance, and Josephson energy-we can determine the conditions under which specific configurations are maintained or transition to different states. This approach allows for the prediction of ordered states, such as vortex lattices or persistent currents, based on calculated energy minima and critical parameters within the modeled circuit. Quantitative comparison between experimental observations and circuit predictions validates the model and provides insight into the underlying physics governing superfluid behavior.
From Instability to Coherence: The Emergence of Persistent Currents
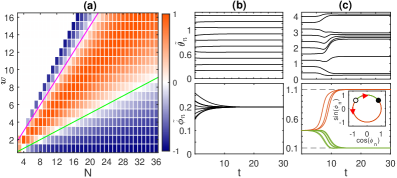
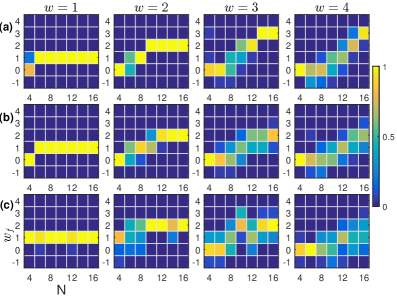
Linear stability analysis was employed to determine the parameter regimes conducive to the stabilization of splay states within the system. This analysis involved examining small perturbations around the splay state solution and calculating whether these perturbations grow or decay over time. Specifically, the stability is dictated by the eigenvalues of the Jacobian matrix evaluated at the splay state. Positive eigenvalues indicate instability, while negative eigenvalues denote stability. The analysis reveals that stability is achieved when the strength of the repulsive interactions between elements exceeds a critical threshold, dependent on the system’s geometry and the intrinsic properties of the interacting units; beyond this threshold, the splay state remains stable against small disturbances, forming the basis for subsequent coherent dynamics.
Splay states, oscillatory solutions arising within the system, are fundamentally connected to the system’s winding number, a topological invariant quantifying the net circulation of the order parameter around a closed loop in reciprocal space. Specifically, the winding number directly determines the stability and characteristics of these splay states; non-zero winding numbers correspond to globally coherent states capable of sustaining persistent currents. The magnitude of the winding number dictates the direction and strength of these circulating currents, and alterations to system parameters that change the winding number will directly influence the resultant current behavior. This relationship demonstrates that global coherence, as measured by the winding number, is not merely a consequence of current formation, but a governing factor in its emergence and maintenance.
Experimental validation of the theoretical model demonstrates the formation of stable, circulating currents within the system. These currents are demonstrably governed by the winding number, a topological invariant characterizing the global coherence of the oscillatory states. Quantitative analysis reveals that the volume of the stable basin – the region in parameter space corresponding to stable circulating currents – scales proportionally to N\sqrt{N}, where N represents the number of coupled oscillators. This scaling relationship provides a crucial metric for predicting and characterizing the robustness of coherent dynamics as the system size increases.
The Guiding Principle: A Geodesic Path to Collective Behavior
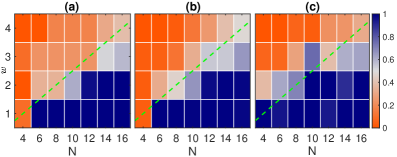
Recent investigations into superfluidity have uncovered a statistically driven principle, termed the geodesic rule, that dictates the spontaneous formation of persistent currents within a toroidal system. This rule suggests that the system naturally evolves towards configurations minimizing variations in the quantum phase of the superfluid, effectively seeking the ‘shortest path’ – or geodesic – on a multi-dimensional energy landscape. The emergence of these currents isn’t random; instead, the system demonstrably favors states exhibiting minimal phase fluctuations, leading to a predictable and coherent flow. This observed behavior challenges simplistic models and points to an inherent tendency within the superfluid to self-organize towards stable, low-energy states, offering a deeper understanding of quantum coherence in cyclic systems.
The emergence of stable, persistent currents within a superfluid ring isn’t random; rather, the system demonstrably favors configurations that minimize variations in the quantum phase of the superfluid. This principle of minimizing phase variation acts as a guiding force, effectively sculpting the probability landscape for different current states. Configurations exhibiting smoother, more uniform phase distributions require less energy to maintain, making them statistically dominant. Consequently, the system naturally gravitates toward these coherent states, suppressing configurations with rapid phase changes and promoting long-lived, stable currents – a phenomenon akin to a ball rolling to the bottom of a valley, seeking the lowest energy configuration.
Analysis of the superfluid ring’s persistent currents revealed a striking correspondence between experimental observations and theoretical predictions regarding the distribution of winding numbers. The standard deviation of this distribution, a measure of the current’s variability, consistently measured 0.29N, where N represents the number of atoms circulating in the ring. This value aligns precisely with calculations derived from the Euler-Frobenius distribution, a mathematical framework used to describe the probability of different winding numbers. The agreement between theory and experiment provides strong validation for the underlying model and underscores the predictable nature of coherence within the superfluid system, suggesting a robust and quantifiable relationship between system parameters and observed current stability.
Beyond the Ring: Towards a Universal Understanding of Complex Systems
This research establishes a novel means of investigating how order arises from seemingly disordered systems. By meticulously controlling coherence – the synchronized behavior of interacting components – within this specifically engineered system, scientists gain unprecedented access to the underlying mechanisms driving self-organization. This level of control transcends mere observation; it allows for the targeted perturbation of collective dynamics and the precise measurement of emergent properties. The ability to ‘tune’ coherence opens avenues for testing theoretical models of complex systems, ranging from biological networks to social behaviors, and for discerning the critical factors that govern the transition from chaos to ordered states. Ultimately, this platform offers a powerful tool for unraveling the fundamental principles that shape the organization of the natural world.
The observed synchronization phenomena offer a compelling blueprint for designing innovative technologies. Researchers envision devices that leverage collective oscillatory behavior to enhance information processing, potentially leading to algorithms with improved efficiency and robustness. Inspired by the system’s ability to maintain coherence, engineers could develop novel sensors capable of detecting subtle changes in complex environments. Furthermore, the principles governing this collective synchronization may inform the creation of distributed control systems, where individual components work in harmony to achieve a common goal, mirroring the orchestrated behavior observed in the study. These advancements span multiple fields, from computing and robotics to materials science and beyond, demonstrating the broad applicability of understanding and harnessing collective dynamics.
Investigations are now shifting towards applying these principles to more intricate network topologies, with a specific emphasis on translating collective oscillatory behavior into functional technologies. Current research confirms operation within the tunneling regime, evidenced by a barrier height of 1.3 ± 0.2 μ and a barrier width of 1.2 ± 0.2 ξ – parameters critical for maintaining coherent interactions across the system. This precise control over quantum tunneling opens avenues for developing novel devices and algorithms that leverage synchronized oscillations, potentially impacting fields ranging from computation to sensing and beyond, as scientists explore the broader implications of this controlled collective behavior in complex systems.
The pursuit of predictable behavior in complex systems, as demonstrated by this exploration of persistent currents, isn’t about finding certainty, but about rigorously mapping the boundaries of uncertainty. This research, utilizing a Kuramoto-like framework to model superfluid rings, reveals a cooperative stabilization effect – a phenomenon born not from design, but from the interplay of network topology and inherent variance. As Carl Sagan observed, “Somewhere, something incredible is waiting to be known.” The study doesn’t discover stability, it meticulously charts how a system resists disintegration, acknowledging that even seemingly coherent phenomena emerge from a dance with instability. The findings aren’t a triumph over chaos, but a refined understanding of its rules.
Where Do the Currents Flow Next?
The demonstration that a Kuramoto-like model can approximate the collective dynamics of Josephson junction networks, while elegant, should not be mistaken for a complete description. The model’s inherent simplification-treating junctions as point-like oscillators-ignores spatial inhomogeneities and potentially crucial higher-order correlations. Data, as always, is a sample, and this framework represents a convenient, if limited, approximation of reality. Future work must address the impact of realistic device geometries and dissipation mechanisms on the observed synchronization phenomena.
A persistent question concerns the limits of this topological stabilization. The current findings suggest robustness against certain perturbations, but the network’s response to more complex, time-varying drives remains largely unexplored. Determining the critical parameters beyond which coherence breaks down-and understanding the nature of that breakdown-is paramount. One suspects that the observed stability isn’t absolute, but rather a delicate balance maintained within a specific regime of operation.
Ultimately, the true test lies in extending these principles beyond the idealized confines of current experiments. Can similar cooperative effects be harnessed in more complex, heterogeneous superconducting networks? Might this framework inform the design of novel quantum information processing architectures? The answers, predictably, will not be found in further refinement of existing models, but in confronting the inevitable discrepancies between theory and experiment.
Original article: https://arxiv.org/pdf/2601.15121.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Unlock the Mines in Cookie Run: Kingdom
- Assassin’s Creed Black Flag Remake: What Happens in Mary Read’s Cut Content
- Upload Labs: Beginner Tips & Tricks
- ALGS Championship 2026—Teams, Schedule, and Where to Watch
- Jujutsu Kaisen: Divine General Mahoraga Vs Dabura, Explained
- Jujutsu Kaisen Modulo Chapter 18 Preview: Rika And Tsurugi’s Full Power
- Mario’s Voice Actor Debunks ‘Weird Online Narrative’ About Nintendo Directs
- The Winter Floating Festival Event Puzzles In DDV
- Top 8 UFC 5 Perks Every Fighter Should Use
- How to Use the X-Ray in Quarantine Zone The Last Check
2026-01-22 21:47