Safe Flight: Reinforcement Learning Takes on Quadrotor Control

Author: Denis Avetisyan

A new framework combines Koopman operator theory and Lyapunov stability constraints to dramatically improve the safety and precision of quadrotor trajectory tracking.

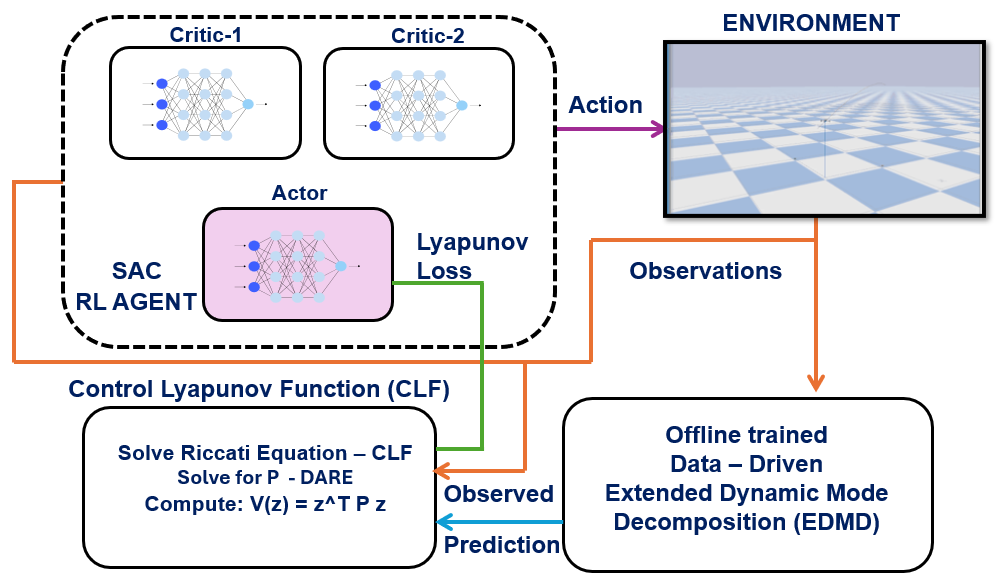
A Lyapunov-based Soft Actor-Critic (SAC) methodology is proposed, integrating stability analysis to refine reinforcement learning and ensure controlled policy optimization.

Lyapunov Constrained Soft Actor-Critic (LC-SAC) leverages model-based reinforcement learning for robust and safe quadrotor control.

While reinforcement learning excels at complex decision-making, ensuring stability in safety-critical systems remains a significant challenge. This work introduces a novel approach, ‘Lyapunov Constrained Soft Actor-Critic (LC-SAC) using Koopman Operator Theory for Quadrotor Trajectory Tracking’, which integrates Lyapunov stability constraints with the Soft Actor-Critic algorithm via a linear system approximation derived from Koopman operator theory. The proposed LC-SAC framework demonstrably improves training convergence and reduces Lyapunov stability violations during quadrotor trajectory tracking. Could this combination of techniques offer a pathway towards more robust and reliable control of nonlinear dynamic systems in real-world applications?

Navigating Complexity: The Challenge of Precise and Stable Control

The successful operation of complex systems, exemplified by the increasingly prevalent quadrotor, fundamentally relies on the ability to not only follow a desired path – precise trajectory tracking – but also to maintain equilibrium during operation and recover from external disruptions – stability guarantees. Achieving both simultaneously presents a significant engineering challenge; a quadrotor, for instance, is subject to aerodynamic drag, wind gusts, and the intricacies of its own rotational dynamics. Consequently, control systems must anticipate and counteract these forces, ensuring the vehicle remains on course and avoids uncontrolled maneuvers. This demands sophisticated algorithms capable of continuously monitoring the system’s state, predicting future behavior, and adjusting control inputs with speed and accuracy, ultimately enabling reliable and predictable performance in dynamic, real-world environments. $\dot{x} = f(x, u)$ represents this need for continuous state updates and control input adjustments.

Conventional control strategies, while effective for simpler systems, frequently encounter limitations when applied to the intricate, nonlinear dynamics inherent in many real-world applications. These methods often rely on linear approximations, which can degrade significantly as a system deviates from its operating point or encounters external disturbances – such as wind gusts for a quadrotor, or friction in robotic joints. This susceptibility to nonlinearity and disturbance leads to performance issues like tracking errors, instability, and ultimately, unreliable operation. Consequently, advanced control techniques are needed to compensate for these effects and ensure robust, precise control in challenging environments, moving beyond the constraints of purely linear approaches.

Extended Dynamic Mode Decomposition (EDMD) accurately predicts tracking errors in position and velocity within the XZ plane.

Safety as a Constraint: Formulating Control Problems for Critical Systems

Formulating control problems as Constrained Markov Decision Processes (CMDPs) is essential for safety-critical systems due to its ability to explicitly handle limitations on system behavior. A standard Markov Decision Process (MDP) aims to maximize cumulative reward; a CMDP extends this by introducing constraints on the expected cumulative cost, denoted as $E[\sum_{t=0}^{\in fty} c(x_t, a_t)] \leq d$ , where $c$ represents the cost function, $x_t$ is the state at time $t$ , $a_t$ is the action, and $d$ is the allowable cost limit. Additionally, CMDPs incorporate constraints that ensure the system state remains within a defined safe set, often expressed as $P(x_t \in X_{safe}) \geq 1 - \epsilon$ , where $X_{safe}$ is the safe set and ε represents an acceptable probability of constraint violation. This formulation allows for the direct optimization of policies that not only achieve a desired objective but also demonstrably satisfy pre-defined safety criteria, critical for applications where even a single violation can have severe consequences.

Lagrangian Relaxation and the Primal-Dual Method are iterative techniques employed to solve Constrained Markov Decision Processes (CMPDs) by decomposing the original problem into a series of more manageable subproblems. Lagrangian Relaxation introduces Lagrange multipliers to incorporate constraints into the objective function, creating a relaxed problem that is often easier to solve. The Primal-Dual Method then iteratively updates both the primal variables (control actions) and the dual variables (Lagrange multipliers) to converge towards a feasible and optimal solution. This approach allows for the computation of saddle points, ensuring that constraint violations are minimized while optimizing the control policy. The iterative nature of these methods is particularly beneficial in reinforcement learning contexts, facilitating safe exploration by penalizing constraint violations and guiding the agent towards feasible solutions during training. The methods effectively address the trade-off between performance and safety in complex control tasks.

The performance of Lagrangian Relaxation and Primal-Dual methods in constrained optimization is predicated on the availability of precise system models. Highly nonlinear systems present a significant challenge to model accuracy, as linearization techniques or simplified assumptions often introduce errors that propagate through the optimization process. These modeling inaccuracies can lead to suboptimal control policies or, critically, solutions that violate safety constraints despite appearing feasible based on the model. Acquiring or learning sufficiently accurate models for such systems typically requires substantial data collection, computationally expensive system identification procedures, or the development of robust estimation techniques to account for model uncertainty.

Learning from Data: Harnessing Nonlinear Dynamics with Koopman Operator Theory

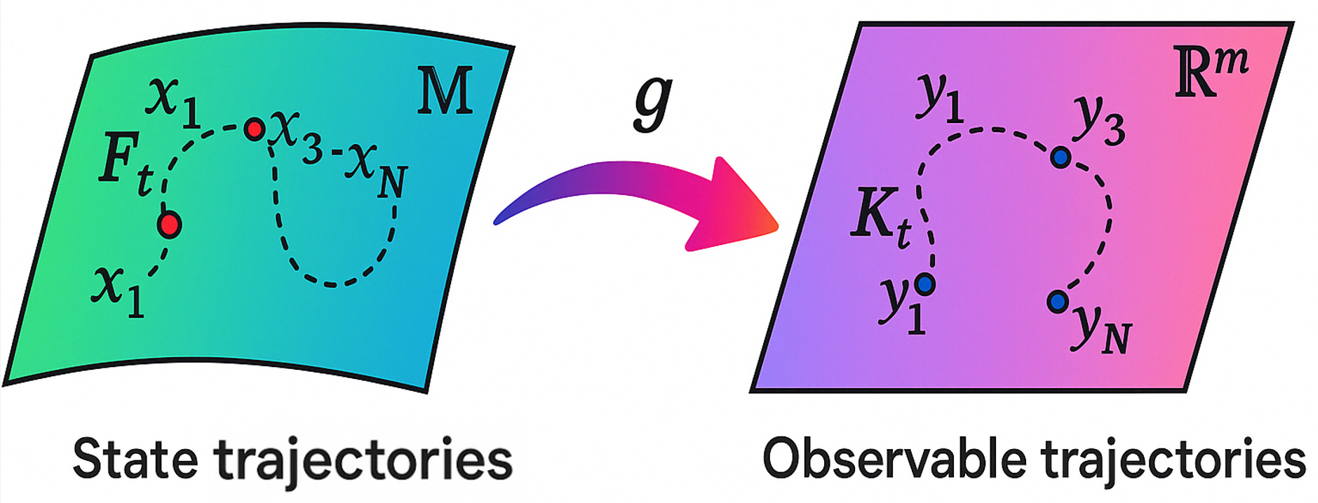
Koopman Operator Theory provides a method for representing the dynamics of nonlinear systems as linear operators acting on an infinite-dimensional space of observable quantities. This is achieved through a transformation that maps the original nonlinear system’s state space to a potentially infinite-dimensional space where the governing dynamics become linear. Specifically, the Koopman operator $L$ maps observables $\Psi(x)$ to their time evolution, such that $L\Psi(x) = \dot{\Psi}(x)$ . By linearizing the system’s dynamics in this observable space, standard linear control techniques-like Linear Quadratic Regulator (LQR) or Model Predictive Control (MPC)-can be applied, offering a pathway to control nonlinear systems using well-established linear methods. The key advantage lies in its ability to handle nonlinearities without requiring explicit knowledge of the nonlinear system’s equations, focusing instead on the system’s observable behavior.

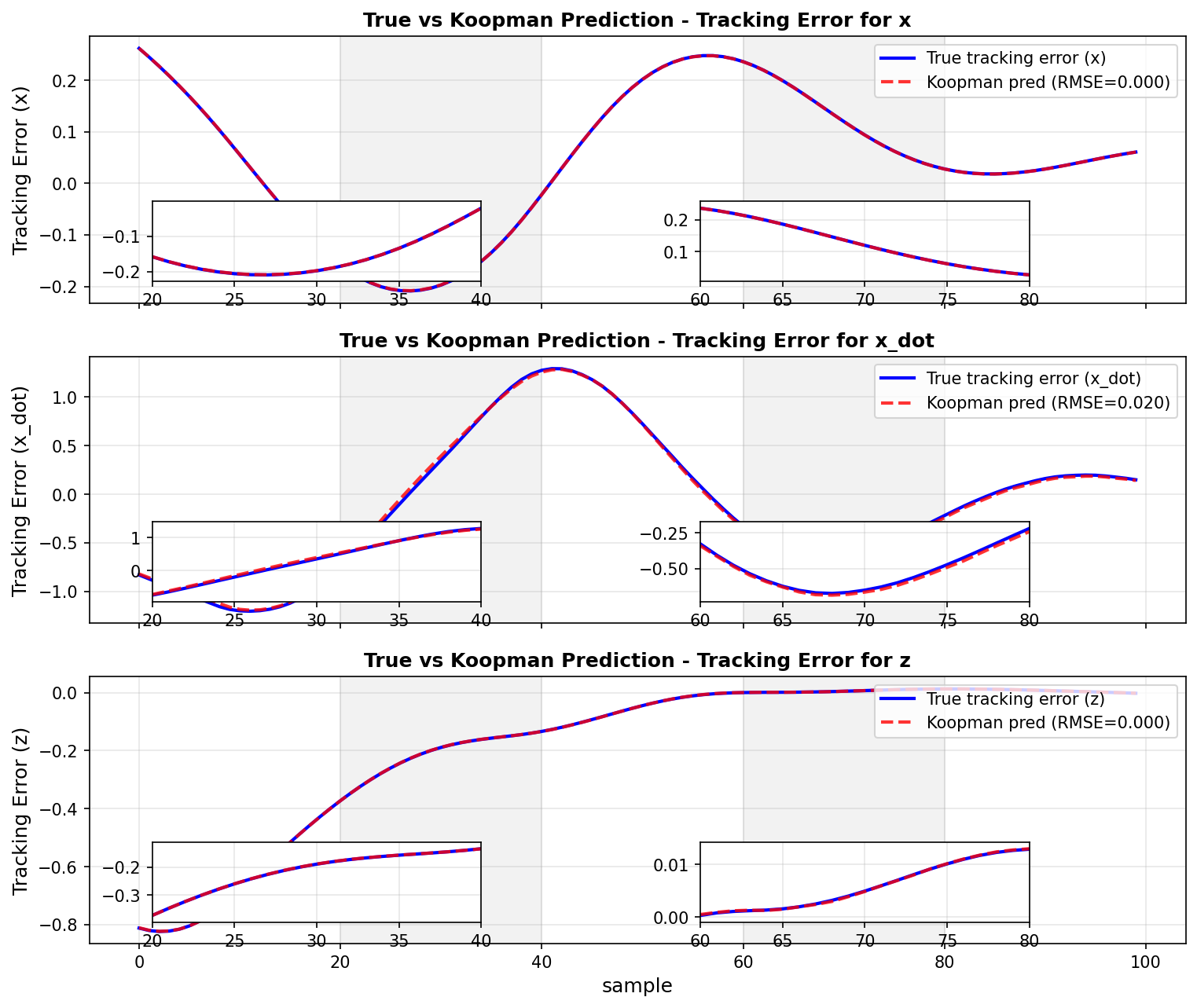
Extended Dynamic Mode Decomposition (EDMD) is a data-driven technique used to approximate the Koopman operator without requiring a predefined mathematical model of the system. EDMD operates by constructing a set of observable quantities from time-series data, then applying a least-squares regression to identify a linear operator that best predicts the future state of these observables. This resulting linear operator serves as an approximation of the infinite-dimensional Koopman operator, allowing linear control techniques to be applied to the original nonlinear system. The accuracy of the EDMD approximation is dependent on the selection of appropriate observables and the quantity of training data; higher-order observables can capture more complex dynamics but also increase the computational cost. Unlike traditional system identification methods, EDMD does not explicitly construct a governing equation; instead, it directly learns the operator that maps the current state to a future state in a chosen observable space.

Integrating Extended Dynamic Mode Decomposition (EDMD) with the Soft Actor-Critic (SAC) reinforcement learning algorithm enables the development of control policies that prioritize safety during the learning process. SAC is an off-policy algorithm that maximizes expected reward while also minimizing entropy, promoting exploration and robustness. When coupled with EDMD, which provides a data-driven system model, SAC can leverage this model to predict system behavior and anticipate potential safety violations. This allows the algorithm to incorporate safety constraints directly into the reward function or action space, effectively penalizing actions that lead to unsafe states. The resulting control policies are thus learned efficiently from data while demonstrably respecting predefined safety boundaries, avoiding the need for explicit, hand-tuned safety layers.

The Koopman operator maps state trajectories <span class="katex-eq" data-katex-display="false">x_t</span> to observable trajectories <span class="katex-eq" data-katex-display="false">y_t = g(x_t)</span>, effectively linearizing nonlinear dynamics in a high-dimensional space. — The Koopman operator maps state trajectories $x_t$ to observable trajectories $y_t = g(x_t)$ , effectively linearizing nonlinear dynamics in a high-dimensional space.

Guaranteeing Stability: Leveraging Lyapunov Theory for Robust Control

Lyapunov Theory offers a powerful and mathematically sound approach to understanding whether a dynamical system – anything that changes over time, from a simple pendulum to a complex robot – will return to a stable state after being disturbed. At its core, the theory centers on identifying a scalar function, often called a Lyapunov function, that decreases monotonically as the system approaches an equilibrium point. If such a function can be found, it definitively proves the system’s stability – a crucial property for ensuring safe and predictable operation in real-world applications. This isn’t merely about preventing oscillations or runaway behavior; it’s about providing a formal guarantee that the system will remain within acceptable bounds, even in the face of external disturbances or uncertainties. The strength of Lyapunov Theory lies in its ability to analyze stability without needing to fully solve the system’s equations of motion, making it invaluable for complex systems where analytical solutions are impossible to obtain.

A control Lyapunov function serves as a powerful tool in control system design, offering a mathematically rigorous pathway to ensuring stability. This function, decreasing monotonically along system trajectories, effectively demonstrates that the system will not diverge from a desired equilibrium point. Crucially, it doesn’t merely imply stability; it provides a verifiable ‘certificate of safety’ – a formal proof that the designed control policy will maintain stable operation under defined conditions. By carefully constructing such a function, engineers can confidently deploy control algorithms in safety-critical applications, knowing that the system’s behavior is demonstrably bounded and predictable, regardless of disturbances or uncertainties. This approach moves beyond empirical testing, offering a guarantee of performance based on established mathematical principles.

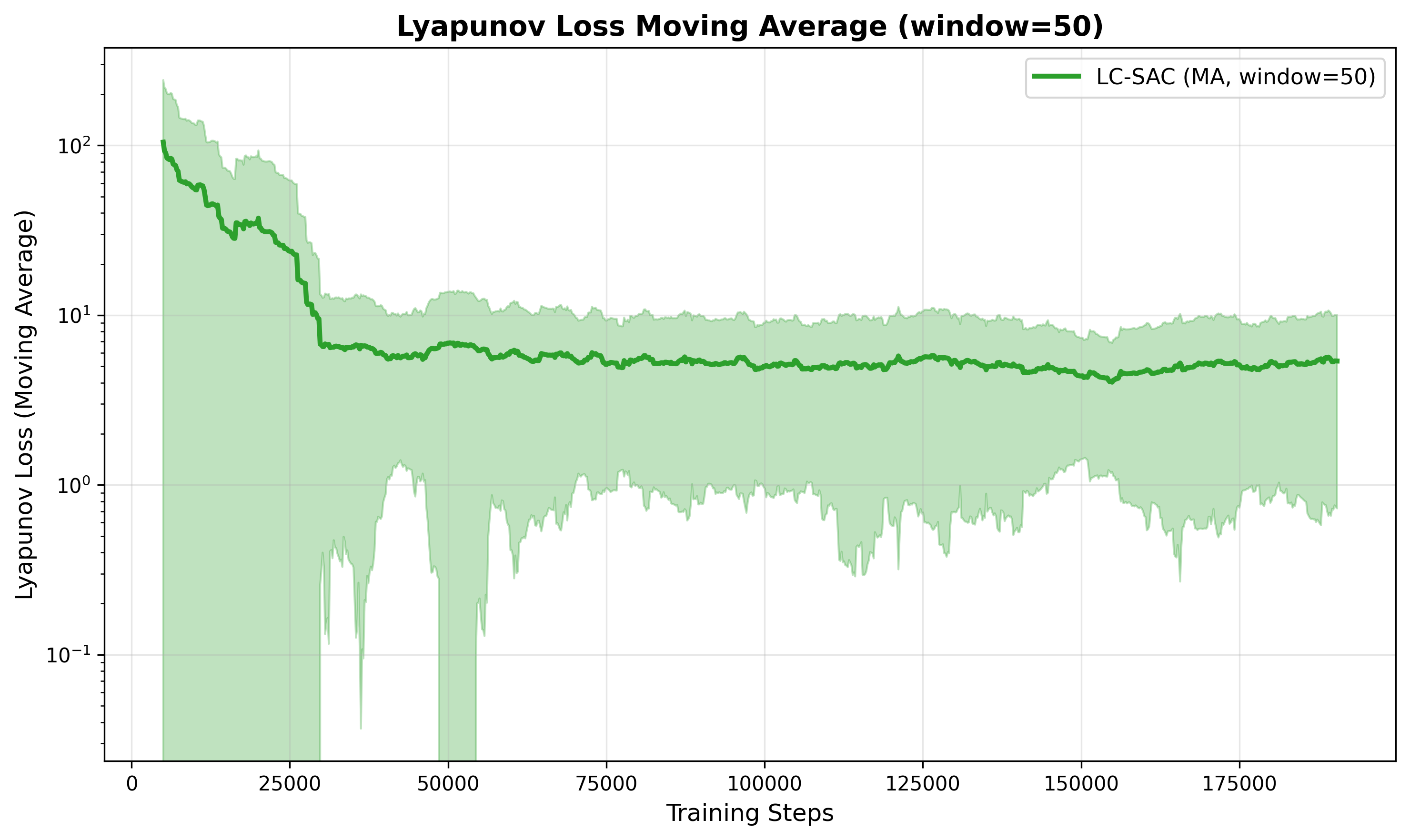
Integrating Lyapunov Function analysis into the Soft Actor-Critic (SAC) framework demonstrably improves the robustness and reliability of learned control policies. This approach effectively introduces a mathematical guarantee of stability, resulting in significantly enhanced performance – evaluation returns were substantially higher and more consistent when compared to a standard SAC algorithm, as evidenced by the presented figures. Crucially, the Lyapunov Loss, a direct measure of stability, not only decreased throughout training but also exhibited a notable stabilization, indicating that the learned policies were consistently maintaining stable behavior and resisting potentially destabilizing influences. This stabilization of the Lyapunov Loss serves as a valuable indicator of the improved safety and predictability of the control policies learned through this integrated framework.

The Lyapunov loss consistently decays across five trials, demonstrating the stability of the LC-SAC algorithm.

Towards Resilient Automation: Charting a Course for Adaptive and Intelligent Systems

The pursuit of robust control systems increasingly demands a shift towards adaptability. Traditional control methods often struggle when confronted with real-world unpredictability – unexpected disturbances, evolving dynamics, or entirely novel situations. Future research prioritizes the development of adaptive control strategies, systems capable of autonomously modifying their behavior in response to changing circumstances. These strategies move beyond pre-programmed responses, instead leveraging real-time data and intelligent algorithms to maintain stability and performance. This necessitates exploration of techniques allowing a controller to identify shifts in system characteristics or external conditions and then recalibrate its parameters accordingly, ensuring continued reliable operation even when faced with the unforeseen. Ultimately, the goal is to create controllers that don’t simply react to disturbances, but proactively anticipate and accommodate them, paving the way for truly resilient and autonomous systems.

Resilient control systems, capable of unwavering performance amidst complexity, are emerging from the synergistic combination of three powerful methodologies. Data-driven modeling leverages the wealth of information generated by real-world operation to create accurate system representations, even when traditional physics-based approaches fall short. This data is then fed into reinforcement learning algorithms, which allow the system to autonomously learn optimal control policies through trial and error. Crucially, these learned policies aren’t simply implemented; they are rigorously validated using Lyapunov stability analysis, a mathematical technique guaranteeing the system’s long-term stability and preventing catastrophic failures. This integrated approach moves beyond reactive control, enabling systems to proactively adapt to unforeseen disturbances and maintain reliable operation in truly uncertain environments, offering a pathway towards robust automation in diverse applications.

The convergence of adaptive control, data-driven modeling, and reinforcement learning extends far beyond theoretical advancements, holding the potential to fundamentally reshape fields reliant on robust automation. Autonomous vehicles, for instance, could navigate unpredictable real-world conditions with increased safety and efficiency, moving beyond pre-programmed routes to truly respond to dynamic environments. Similarly, in the realm of medical robotics, these techniques promise more precise and adaptable surgical tools, enabling minimally invasive procedures with greater accuracy and reduced risk to patients. Beyond transportation and healthcare, applications span industrial automation, aerospace engineering, and even disaster response, where robots equipped with resilient control systems could operate effectively in chaotic and uncertain situations – ultimately leading to increased reliability, enhanced performance, and the unlocking of capabilities previously considered unattainable in complex systems.

The pursuit of increasingly sophisticated algorithms, as demonstrated by the Lyapunov Constrained Soft Actor-Critic framework, echoes a fundamental tension. This research, blending Koopman operator theory with reinforcement learning for quadrotor trajectory tracking, highlights the necessity of embedding ethical considerations directly into the automated systems themselves. As Blaise Pascal observed, “Man is but a reed, the most fragile thing in nature; but he is a thinking reed.” The ‘thinking’ aspect-the intentional design incorporating Lyapunov stability constraints-is crucial. Without such foresight, the acceleration of algorithmic prowess, while impressive, risks producing systems adrift from meaningful direction, much like an unconstrained trajectory. Data becomes the mirror, algorithms the artist’s brush, and society the canvas, yet every model remains a moral act.

What Lies Ahead?

The pursuit of safe reinforcement learning, as exemplified by Lyapunov Constrained Soft Actor-Critic, inevitably confronts a fundamental tension. Scalability is readily achieved through abstraction; safety, however, demands relentless attention to detail, a granular understanding of the system’s limits. The integration of Koopman operator theory offers a powerful means of modeling complex dynamics, yet this modeling itself encodes assumptions, a particular worldview baked into the algorithm. The true measure of progress will not be simply faster trajectory tracking, but a demonstrable reduction in the implicit biases embedded within these automated systems.

Current approaches often treat safety as a post-hoc constraint, a box ticked after the learning process. A more robust paradigm demands that privacy and stability are not merely performance metrics, but foundational design principles. Future work must grapple with the question of verifiable safety-how to provide guarantees, not just probabilistic assurances, that a system will behave predictably in unforeseen circumstances. The challenge extends beyond the technical; it requires a rigorous ethical accounting of the values being automated.

Ultimately, the success of this line of inquiry will hinge on a shift in focus. The emphasis must move from maximizing performance to minimizing unintended consequences. Every automated decision, every optimized trajectory, reflects a choice. The field must acknowledge that acceleration without direction is not progress, but a race toward increasingly complex and potentially catastrophic failure.

Original article: https://arxiv.org/pdf/2602.04132.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/