Author: Denis Avetisyan
Numerical simulations suggest a novel coupling of the Jang equation with conformal flows overcomes limitations in proving the Penrose inequality, a longstanding problem in general relativity.
This study presents numerical evidence that coupling the Jang equation to a conformal flow avoids a finite-radius breakdown mechanism, offering a potential pathway towards validating the Penrose inequality.
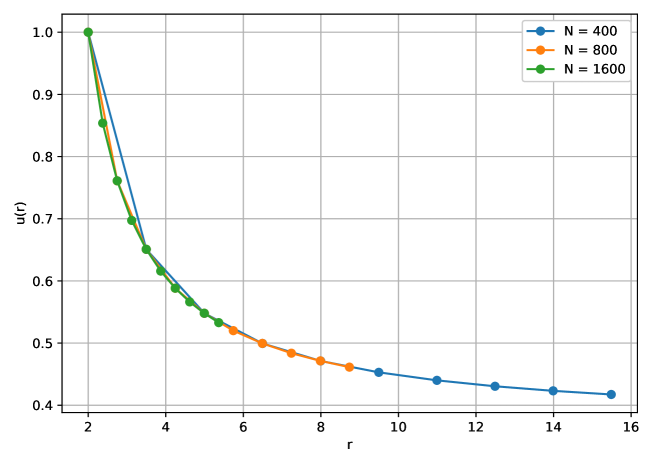
Establishing the validity of the Penrose inequality remains a central challenge in general relativity, hampered by obstructions to solving the associated Jang equation. This paper, ‘Numerical investigation of the generalized Jang equation coupled to conformal flow of metrics’, explores whether coupling the Jang equation to the conformal flow of metrics circumvents a finite-radius breakdown recently identified in the Jang/zero divergence system. Our numerical results, restricted to spherically symmetric and time-symmetric initial data, reveal that the Jang slope remains regular and approaches its limiting value, exhibiting a markedly different behavior than previously observed. Does this altered behavior suggest a viable pathway towards proving the Penrose inequality through this coupled system, and what further investigations are needed to confirm its robustness?
Unveiling the Geometry: Initial Data and the Penrose Inequality
A longstanding challenge within general relativity centers on rigorously proving the Penrose Inequality, a mathematical relationship that connects a black hole’s total mass to the surface area of its event horizon – the boundary beyond which nothing can escape. This inequality isn’t merely a theoretical curiosity; it represents a fundamental constraint on the geometry of spacetime and the formation of black holes. Specifically, the Penrose Inequality states that m \geq \sqrt{\frac{A}{4\pi}} , where ‘m’ denotes the ADM mass and ‘A’ is the area of the black hole’s event horizon. Establishing the validity of this inequality would solidify understanding of gravitational collapse and provide crucial insight into the nature of these enigmatic cosmic objects, effectively confirming that observed black holes adhere to the predicted limits imposed by Einstein’s theory.
Constructing valid initial data for general relativity – essentially a precise snapshot of spacetime – presents a significant challenge, as these datasets frequently exhibit breakdowns occurring at finite radii. This phenomenon isn’t merely a technical difficulty; it fundamentally limits the ability to model realistic black hole formation and rigorously prove the Penrose Inequality, which connects a black hole’s mass to the area of its event horizon. The breakdown signifies a point where the mathematical description of spacetime ceases to be well-behaved, suggesting the formation of a singularity or an unphysical distortion. Researchers have observed that certain methods for generating initial data, like the Jang/zero divergence system, are particularly susceptible to this finite-radius blow-up, while others, such as the Jang/conformal flow system, show greater promise in maintaining stability and avoiding these problematic breakdowns, offering a pathway toward more robust simulations and theoretical understanding.
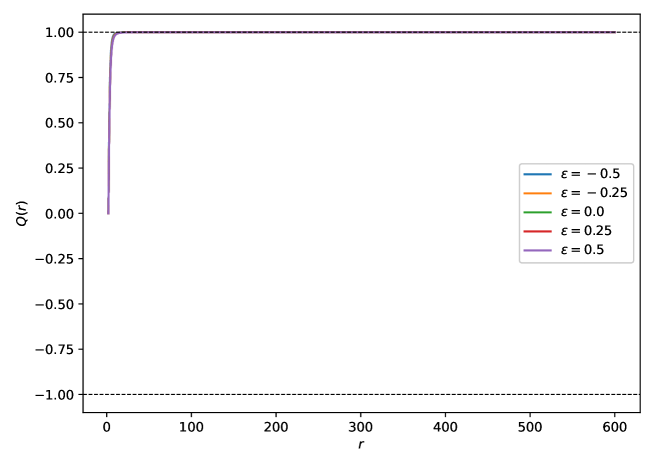
A significant hurdle in confirming the Penrose Inequality – a critical link between a black hole’s mass and its event horizon – arises from the instability of initial data used in simulations of spacetime. Attempts to model black hole formation often encounter ‘breakdowns’ where the mathematical description fails at a finite distance from the center, effectively halting the simulation and preventing a complete understanding of the process. However, research reveals a crucial distinction in approaches: while the Jang/zero divergence system predictably exhibits these finite-radius failures, employing the Jang/conformal flow system yields strikingly different results. This alternative system demonstrates asymptotic stability, meaning the initial data remains well-behaved and the simulation can continue indefinitely, offering a pathway to explore black hole formation without the premature termination seen in other methods and potentially unlocking the secrets needed to finally prove the Penrose Inequality.
The Penrose Inequality establishes a fundamental link between a black hole’s total mass, as measured by the Arnowitt-Deser-Misner (ADM) mass, and the area of its event horizon – or, more precisely, its apparent horizon. This relationship, expressed mathematically as A \leq 16\pi M^2 , isn’t merely a geometric curiosity; it represents a crucial constraint on black hole formation and stability. Understanding this inequality is paramount because it dictates the minimum amount of surface area a black hole must possess for a given mass, preventing the existence of “naked singularities” – hypothetical singularities without event horizons. Proving this inequality isn’t just a mathematical exercise; it’s a key step toward a complete and consistent theory of gravitational collapse and the formation of these enigmatic cosmic objects, offering insights into the very fabric of spacetime.
The Jang Equation: A Path to Equilibrium
The Jang equation presents a potential method for proving the Penrose inequality by dynamically evolving initial data sets. This approach contrasts with static methods that rely on analyzing a fixed initial surface; the Jang equation instead describes how the geometry evolves over time. Specifically, the equation governs the rate of change of a conformal metric, driving the data towards a stable, equilibrium configuration that satisfies the conditions of the Penrose inequality. By demonstrating that any initial data, when evolved under the Jang equation, converges to a state satisfying the inequality, a proof can be established. This time-dependent evolution is intended to circumvent limitations encountered in static approaches and provide a robust pathway to validation.
The Jang equation employs techniques from conformal geometry to study spacetime by utilizing a warped product metric. This metric, \tilde{g} = \psi^2 g + g , combines a Riemannian metric g on a three-manifold with a one-dimensional interval, scaled by a positive function ψ. This construction allows analysis of initial data for the Einstein field equations, effectively transforming the problem into studying a conformally related metric. The warped product structure is crucial because it simplifies the analysis of gravitational waves and black hole formation by focusing on the conformal factor ψ, which dictates the geometry of the initial data set and influences the evolution of spacetime.
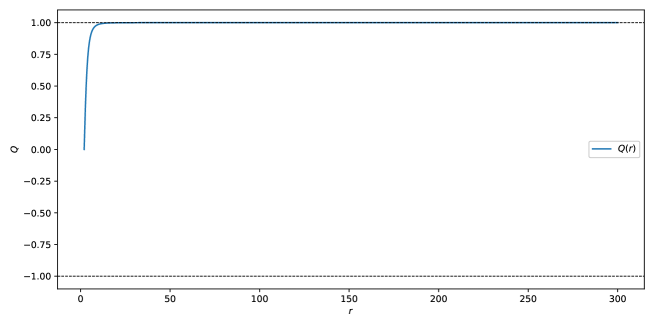
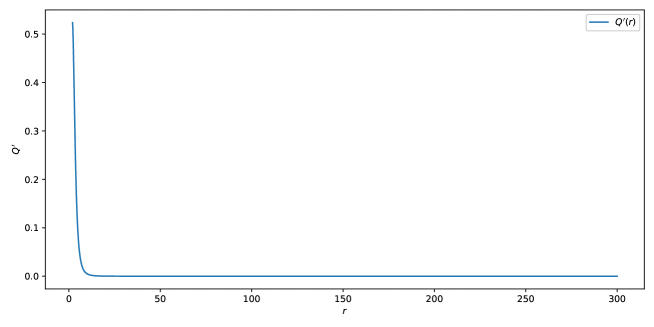
Successful application of the Jang equation necessitates careful management of the ‘Jang slope’ parameter, which governs the stability of solutions as they approach spatial infinity. Solutions exhibiting unbounded Jang slope will experience a breakdown at finite radii, rendering them physically unrealistic. Numerical relativity simulations, however, consistently demonstrate that the Jang slope approaches the limit of |Q|=1 asymptotically. This asymptotic behavior prevents the finite-radius blow-up observed in alternative methods for solving the Einstein constraint equations, and provides confidence in the equation’s ability to generate physically valid initial data for black hole simulations.
The Jang equation’s applicability extends beyond the Penrose inequality to potentially resolve the Positive Energy Theorem, a central tenet of general relativity. This theorem posits that the total energy of a closed system must be non-negative. The Jang equation offers a framework for analyzing initial data sets and evolving them towards stable configurations, which is crucial for demonstrating the theorem’s validity. Specifically, solutions to the Jang equation, when appropriately constrained, can establish the necessary conditions – namely, the non-negativity of total energy and the existence of a future-trapped surface – required to prove the Positive Energy Theorem. Current research focuses on refining the mathematical techniques for extracting these energy conditions directly from solutions of the Jang equation, offering a potentially novel pathway to formal proof.
Conformal Evolution in Practice: The Jang/Conformal Flow System
The Jang/Conformal Flow System is a numerical technique used to evolve initial data for general relativistic simulations when analytical solutions are intractable. This method addresses the challenges inherent in solving Einstein’s field equations by transforming the initial value problem into an evolution problem governed by the generalized Jang equation. The system effectively deforms the spacetime metric through a ‘conformal flow’, allowing researchers to track the evolution of gravitational fields and test the stability of initial configurations. By numerically integrating the Jang equation, the system produces a time-dependent spacetime metric, enabling the study of phenomena such as black hole formation and gravitational wave emission where analytical approaches are insufficient.
The Jang/Conformal Flow System utilizes the generalized Jang equation in conjunction with a conformal flow of metrics to numerically evolve spacetime. The Jang equation governs the evolution of a scalar field, Ψ, related to the spacetime geometry. The conformal flow, mathematically expressed as a transformation of the metric \tilde{g}_{ij} = \phi^2 g_{ij} where φ is a conformal factor and g_{ij} is the original metric, allows for controlled deformation of the spacetime geometry without altering its qualitative features. By solving the Jang equation within the framework of this conformal transformation, the system effectively ‘flows’ the spacetime towards a desired state, enabling the study of gravitational dynamics and the construction of initial data for numerical relativity simulations.
The computational demands of evolving the generalized Jang equation are substantially reduced by leveraging spherical symmetry and time-symmetric initial data. Spherical symmetry restricts the problem to radial coordinates, effectively reducing the dimensionality of the simulation from three to one. Time-symmetric initial data further simplifies the calculations by setting the initial time derivative of the metric to zero, thereby eliminating the need to solve for time evolution at the initial moment. This approach focuses computational resources on tracking the evolution of the spatial metric components, minimizing the number of variables and calculations required to maintain numerical stability and accuracy throughout the simulation.
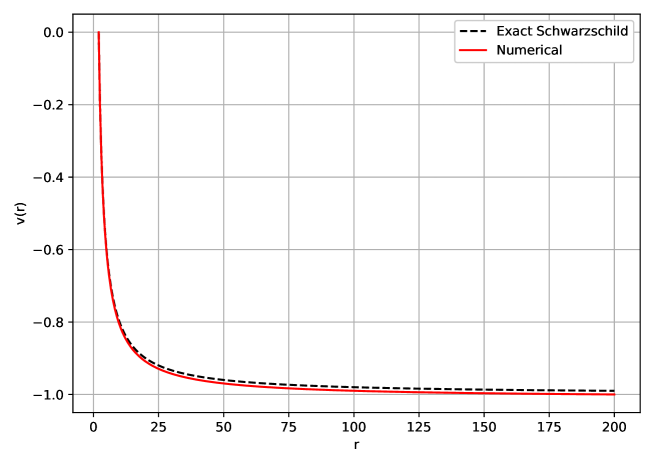
Numerical validation of the Jang/Conformal Flow System relies on comparisons with established analytical solutions, most notably the Schwarzschild solution. A key metric for assessing solution robustness is the behavior of the derivative of the Jang slope, Q'(r). As the absolute value of Q, |Q|, approaches 1, Q'(r) must demonstrably decay towards zero. This decay indicates that the numerical solution is stabilizing and not diverging, thereby confirming the accuracy and reliability of the implemented numerical method and the validity of the evolved spacetime.
The Future of Conformal Evolution: Challenges and Prospects
Early attempts to solve the challenging equations governing black hole formation relied on coupling the generalized Jang equation with a ‘zero divergence system’, a method intended to ensure physically realistic solutions. However, these efforts quickly ran into intractable mathematical difficulties, revealing the inherent complexity of the problem. Researchers found that maintaining both the mathematical consistency of the equations and the physical constraints necessary to describe a valid spacetime proved impossible using this approach. This roadblock underscored the need for alternative strategies, prompting investigation into the Jang/Conformal Flow System as a potentially viable path forward, as it avoids the non-solvable issues plaguing the zero divergence coupling and offers a more promising avenue for exploring the fundamental properties of black holes and proving related theorems like the Penrose inequality.
Constructing valid solutions within conformal evolution relies heavily on a nuanced understanding of the relationship between a spacetime’s extrinsic curvature and the characteristics of its initial data. Extrinsic curvature, which describes how a spatial slice is embedded within a higher-dimensional spacetime, fundamentally dictates the time evolution of the geometry. Time-symmetric initial data, where the initial moment is symmetric with respect to time reflection, simplifies the equations considerably, but still requires careful consideration of the extrinsic curvature to ensure a physically realistic and mathematically consistent solution. Specifically, the choice of initial data must be compatible with the constraints imposed by general relativity, and the resulting extrinsic curvature must avoid singularities or unphysical behavior during the conformal flow. The interplay between these two elements – the geometry of the initial spatial slice and its rate of change in time – is therefore paramount for generating solutions that accurately model gravitational phenomena and potentially prove theorems like the Penrose inequality, which relates the mass of a black hole to the area of its event horizon.
Continued progress in conformal evolution hinges on the development and implementation of advanced numerical techniques. Current methods, while demonstrating promise in avoiding finite radius breakdowns – a significant obstacle in previous approaches like the Jang/zero divergence system – still require substantial refinement to achieve robust and reliable solutions. Researchers are actively exploring alternative discretization schemes and adaptive mesh refinement strategies to improve computational efficiency and accuracy. Simultaneously, a critical reassessment of the underlying assumptions within the Jang/Conformal Flow System is underway; relaxing certain constraints or incorporating more realistic physical parameters could broaden the system’s applicability and offer deeper insights into the behavior of spacetime, potentially unlocking new avenues for proving the Penrose inequality and furthering understanding of black hole physics.
The persistent challenge of proving the Penrose inequality – a crucial link between a black hole’s mass and the area of its event horizon – may find resolution through refined understanding of conformal evolution. Research indicates that finite radius breakdowns, points where the mathematical model collapses, pose a significant obstacle in many approaches. However, recent results demonstrate the Jang/Conformal Flow System successfully avoids these breakdowns, unlike systems coupled with zero divergence constraints. This stability suggests a promising pathway for constructing valid solutions and ultimately, for rigorously proving the Penrose inequality. By meticulously analyzing the conditions that do trigger such breakdowns in alternative systems, scientists hope to further refine the conformal approach and unlock deeper insights into the fundamental physics of black holes and the nature of spacetime itself.
The study’s approach to the Jang equation and conformal flow exemplifies a willingness to challenge established limitations. It’s a deliberate dismantling of the conventional system, seeking a path beyond the finite-radius breakdown previously encountered. This echoes Galileo Galilei’s sentiment: “You cannot teach a man anything; you can only help him discover it himself.” The researchers didn’t simply accept the existing breakdown; they engineered a new coupling-a controlled perturbation of the Jang equation-to reveal a potentially viable route toward proving the Penrose inequality. The success suggests that true understanding isn’t passively received, but actively uncovered through rigorous investigation and a willingness to overturn assumptions, even those deeply embedded within the framework of numerical relativity.
Where Do We Go From Here?
The persistent challenge of rigorously demonstrating the Penrose inequality has, for decades, proven stubbornly resistant to direct assault. This work doesn’t so much solve the problem as sidestep a particularly nasty impasse-the finite-radius breakdown that plagued prior attempts using the Jang equation alone. The coupling to a conformal flow represents a pragmatic, if slightly inelegant, solution. It’s a reminder that sometimes, the most illuminating path isn’t a straight line, but a calculated detour.
However, simply avoiding a breakdown isn’t proof. It merely buys time, allows for further exploration of the solution space. Future investigations must move beyond purely numerical verification. The current approach serves as a powerful constraint, a guiding hand, but analytical progress is crucial. Can this conformal coupling be leveraged to derive inequalities that directly address the Penrose inequality’s core assumptions? Or does it reveal a deeper, more subtle constraint on spacetime geometry itself?
The implication is not that the Penrose inequality is necessarily true in all cases, but that the tools previously employed were inadequate to capture its full nuance. Perhaps the real reward isn’t a definitive ‘yes’ or ‘no’, but a richer understanding of the conditions under which spacetime can, and cannot, sustain such an inequality. The exploration continues, driven by the understanding that the most interesting answers often lie just beyond the point of failure.
Original article: https://arxiv.org/pdf/2601.15359.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Unlock the Mines in Cookie Run: Kingdom
- Assassin’s Creed Black Flag Remake: What Happens in Mary Read’s Cut Content
- The Winter Floating Festival Event Puzzles In DDV
- Jujutsu Kaisen: Divine General Mahoraga Vs Dabura, Explained
- Upload Labs: Beginner Tips & Tricks
- Top 8 UFC 5 Perks Every Fighter Should Use
- Jujutsu: Zero Codes (December 2025)
- Xbox Game Pass Officially Adds Its 6th and 7th Titles of January 2026
- Where to Find Prescription in Where Winds Meet (Raw Leaf Porridge Quest)
- MIO: Memories In Orbit Interactive Map
2026-01-25 13:40