Taming Attention: Stabilizing Transformers for Faster Training

by

Author: Denis Avetisyan

A new approach to controlling attention logit changes enables higher learning rates and improved performance in transformer models.

During training with MLA, the model’s middle head of the middle layer-specifically head 16 and layer 8-exhibited a peak logit value and an average absolute change in logit throughout training when utilizing a base learning rate of $3e-3$.
During training with MLA, the model’s middle head of the middle layer-specifically head 16 and layer 8-exhibited a peak logit value and an average absolute change in logit throughout training when utilizing a base learning rate of $3e-3$.

Parameter-specific learning rates enhance stability and scalability, particularly within efficient multi-latent attention architectures.

Maintaining stable training in transformer models is challenging, particularly given the propensity for unbounded growth in attention weights. This paper, ‘Controlling changes to attention logits’, investigates the critical role of regulating changes to attention logits via parameter-specific learning rates for query and key weights. Our approach enables increased base learning rates, outperforms existing methods in efficient Multi-Latent Attention (MLA) settings, and achieves competitive performance with standard normalization techniques in Multi-Head Attention. Could fine-grained control of attention dynamics unlock even more robust and scalable transformer architectures?

The Fragile Foundation: Instability in Attention Mechanisms

The remarkable performance of transformer models hinges on the attention mechanism, a process allowing the network to weigh the importance of different input elements. However, this very mechanism can introduce significant challenges during training. Specifically, the calculation of $Attention Logits$ – the raw, unnormalized scores determining these weights – is prone to instability. As gradients flow through the attention layers during backpropagation, they can either diminish exponentially – vanishing gradients – or grow without bound – exploding gradients. This phenomenon disrupts the learning process, making it difficult for the model to converge and hindering its ability to generalize effectively. Consequently, scaling transformers to larger datasets and model sizes becomes problematic, necessitating innovative regularization techniques to maintain stable and reliable training.

The pursuit of increasingly powerful transformer models is often hampered by training instability, particularly as model size and dataset scale grow. This instability manifests as exploding or vanishing gradients during the backpropagation process, effectively derailing the learning process. To counteract this, researchers commonly employ regularization techniques, with Gradient Clipping being a prominent example. This method involves limiting the magnitude of gradients during training, preventing them from becoming excessively large and disrupting the optimization. However, simply applying gradient clipping is often insufficient for the demands of large-scale training, necessitating more nuanced and robust approaches to maintain stable learning and unlock the full potential of these advanced architectures.

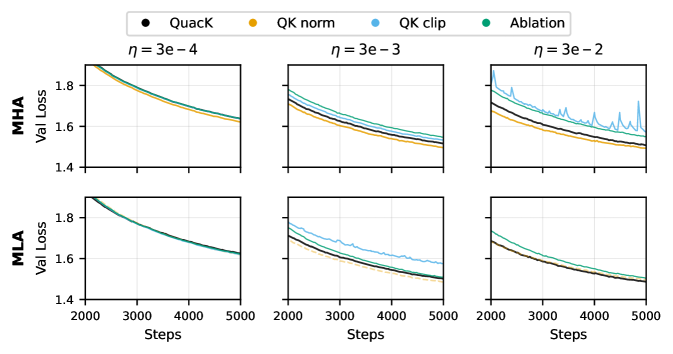
Conventional regularization techniques struggle to address the nuanced instabilities within the attention mechanism during transformer training. Existing methods often apply uniform constraints, failing to differentiate between crucial and inconsequential attention dynamics, and consequently limiting the achievable learning rate. Training large models with a base learning rate of $3e-2$-a value known to accelerate convergence-frequently results in divergence using these standard approaches. However, recent advancements demonstrate the ability to stabilize training at this aggressive learning rate through more targeted interventions, effectively modulating attention dynamics and unlocking the potential for faster and more robust model scaling. This finer-grained control allows for reliable optimization even with larger models and datasets, overcoming a key barrier to achieving state-of-the-art performance.

Stabilizing transformer pretraining requires decreasing the learning rates of query and key weights, as demonstrated by consistently maintained query-key norms across four models trained with a base learning rate of 3e-2.
Stabilizing transformer pretraining requires decreasing the learning rates of query and key weights, as demonstrated by consistently maintained query-key norms across four models trained with a base learning rate of 3e-2.

Controlled Shifts: The Principle of Logit Change

Logit Change Control is a technique designed to improve the stability of attention mechanisms during training. It operates by directly constraining the permissible variation in attention scores-specifically, the logits-between successive training steps. Uncontrolled changes in these logits can lead to instability and hinder convergence. By limiting the magnitude of these changes, the method encourages smoother updates to the attention weights, resulting in more predictable and reliable learning dynamics. This approach focuses on regulating the rate at which attention shifts, rather than directly manipulating the attention weights themselves, providing a principled method for stabilizing the attention process.

Logit change control is implemented by dynamically adjusting the learning rates applied to the $Query Weight$ and $Key Weight$ matrices during training. Specifically, the learning rate for each weight matrix is modulated based on its current norm. A higher norm indicates larger attention scores, triggering a reduction in the learning rate to constrain subsequent updates and prevent drastic changes in attention distributions. Conversely, lower norms allow for larger learning rates, facilitating more substantial updates when attention scores are small. This norm-based modulation effectively stabilizes training by ensuring smoother, more controlled adjustments to attention weights.

Learning Rate Modulation directly facilitates Logit Change Control by dynamically adjusting the step size during training, preventing excessively large shifts in attention scores. This approach contributes to more stable training dynamics and improved convergence. The QuacK method leverages a simplified implementation of Learning Rate Modulation, resulting in an approximate $10\%$ speedup compared to alternative techniques. This efficiency gain is attributable to the reduction in computational overhead associated with the streamlined modulation process, while maintaining equivalent or improved stability characteristics during attention mechanism training.

Training a small model with Algorithm 1 demonstrates that varying the norm used to modulate query and key weight learning rates-specifically, using either Frobenius or spectral norms with different values of τ-results in minimal performance differences as measured by validation loss.
Training a small model with Algorithm 1 demonstrates that varying the norm used to modulate query and key weight learning rates-specifically, using either Frobenius or spectral norms with different values of τ-results in minimal performance differences as measured by validation loss.

Normalization as a Stabilizing Force

Directly normalizing attention activations, as implemented in methods like $QK$ Norm, addresses instabilities that can arise during training of transformer models. This technique applies normalization to the query and key vectors before calculating attention weights, effectively rescaling these activations. By controlling the magnitude of these values, $QK$ Norm prevents excessively large or small activations which can lead to vanishing or exploding gradients. Consequently, this normalization facilitates faster convergence and improves the overall stability of the training process, particularly in models with a large number of parameters or complex architectures. The application of normalization to attention mechanisms helps maintain a more consistent signal flow and allows for the use of higher learning rates without compromising training stability.

The $QK$ Clip strategy enhances attention mechanism stability by imposing upper and lower bounds on the values within the query-key attention matrix. This clipping operation restricts the magnitude of attention weights, preventing excessively large or small values that can contribute to unstable gradients during training. By limiting these weights, $QK$ Clip aims to maintain a more manageable dynamic range for attention scores, promoting smoother convergence and potentially improving generalization performance. Empirical results indicate that, while effective, $QK$ Clip may exhibit slightly lower performance compared to normalization methods like $QK$ Norm, particularly within Multi-Latent Attention (MLA) architectures.

Normalization strategies for attention mechanisms are frequently implemented alongside Multi-Head Attention to enhance both performance and training stability. Weight measurement is commonly performed using the Frobenius Norm and Spectral Norm, providing metrics for regularization and control. In Multi-Latent Attention (MLA) architectures, the QuacK normalization technique demonstrates validation loss that is comparable to or better than that achieved with QK Norm, and consistently outperforms the QK Clip method, suggesting its efficacy in managing attention weight distributions within MLA models.

Training validation losses reveal that QK normalization consistently outperforms other attention mechanisms, offering stability at high learning rates and efficiency with MLA, making it a preferable alternative to QuacK despite QuacK's reasonable performance.
Training validation losses reveal that QK normalization consistently outperforms other attention mechanisms, offering stability at high learning rates and efficiency with MLA, making it a preferable alternative to QuacK despite QuacK’s reasonable performance.

Architectural Refinement: Towards Scalable Intelligence

Multi-Latent Attention presents a significant advancement in reducing the computational burden traditionally associated with transformer models. This approach leverages Down Projection, a technique where the key and value matrices are first projected to a lower dimensionality before attention calculations are performed. By operating in this reduced latent space, the model drastically minimizes the number of parameters and floating-point operations required, leading to faster processing and lower memory consumption. This isn’t simply a matter of compression; the method aims to retain crucial information while discarding redundancy, enabling models to scale more effectively without sacrificing performance. The result is a pathway toward deploying sophisticated transformer architectures on resource-constrained devices and handling significantly larger datasets, ultimately broadening the applicability of these powerful models.

Traditional positional embeddings in transformer models often struggle with extrapolating to sequence lengths exceeding those encountered during training, hindering performance on longer inputs. RoPE – Rotary Positional Embedding – offers a compelling solution by representing positional information through rotation matrices applied to query and key vectors. This innovative approach encodes relative positional differences, allowing the model to generalize effectively to unseen sequence lengths and maintain robust performance. Unlike absolute positional embeddings, RoPE’s relative encoding naturally handles longer sequences, significantly improving the model’s ability to process extended contexts without substantial performance degradation. The method’s inherent properties also contribute to improved efficiency, as the positional information is integrated directly into the attention mechanism, reducing computational overhead and fostering more scalable transformer architectures.

The convergence of architectural refinements and carefully designed training protocols is enabling the development of transformer models with unprecedented scalability and efficiency. By optimizing both the model’s internal structure and the learning process, researchers are overcoming limitations previously encountered when scaling these powerful networks. This synergistic approach not only reduces computational demands-allowing for faster training and deployment-but also unlocks the potential for tackling increasingly complex tasks. The result is a new generation of models capable of processing larger datasets and generating more nuanced outputs, ultimately expanding the scope of applications for artificial intelligence across diverse fields and pushing the boundaries of what’s computationally feasible.

The pursuit of stable training within transformer models, as detailed in the study of attention logit control, echoes a fundamental principle of elegant design. It isn’t about adding complexity to address instability, but about refining the existing structure until only the essential elements remain. As John von Neumann observed, “The best way to predict the future is to invent it.” This resonates with the paper’s approach – proactively controlling the attention logits through parameter-specific learning rates, rather than reactively addressing instability as it arises. The methodology demonstrates an invention of a more predictable training process, allowing for higher learning rates and improved performance, particularly with efficient Multi-Latent Attention (MLA). The work isn’t simply about improving a model; it’s about sculpting a more robust and predictable system.

Where To Next?

The pursuit of stable training in transformer models has, predictably, focused on managing the flux within attention. This work offers a refinement – not a revolution – by acknowledging that all parameters are not created equal. The principle is sound: constrain change where it matters most, and allow freedom elsewhere. However, the question remains whether this parameter-specific approach represents a local optimum in a vastly complex search space. Is ‘logit stability’ a genuinely fundamental constraint, or merely a symptom of deeper instabilities elsewhere in the architecture?

The demonstrated synergy with Multi-Latent Attention (MLA) is intriguing, suggesting a potential path toward efficient scaling. Yet, efficiency alone is a hollow victory if it comes at the cost of representational capacity. Future work must rigorously evaluate whether these constraints, while promoting stability, subtly prune the model’s ability to capture nuanced relationships within data. The elegance of µP scaling hints at underlying mathematical structure, but further exploration is needed to move beyond empirical observation towards a truly principled understanding.

Ultimately, the field confronts a familiar paradox: simplification often yields performance gains, but at the risk of obscuring fundamental truths. The art, then, lies not in adding complexity, but in identifying and excising the unnecessary-a ruthless pursuit of lossless compression, even within the seemingly boundless space of neural networks.

Original article: https://arxiv.org/pdf/2511.21377.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2025-11-29 21:26