Taming Many-Body Chaos: A New Path to Accurate Calculations

Author: Denis Avetisyan

Researchers have developed a novel stochastic method that promises to significantly improve the accuracy and reliability of calculations in complex quantum systems.

The effective number of configurations, <span class="katex-eq" data-katex-display="false"> eSe^{S} </span>, shifts with coupling strength, diverging within specific intervals and demonstrating a sensitivity to perturbative order-a phenomenon suggesting the model's predictive power is not uniform across all parameter regimes. — The effective number of configurations, $eSe^{S}$ , shifts with coupling strength, diverging within specific intervals and demonstrating a sensitivity to perturbative order-a phenomenon suggesting the model’s predictive power is not uniform across all parameter regimes.

Perturbation Theory Quantum Monte Carlo offers a robust approach for high-order many-body calculations, addressing challenges in strongly correlated systems.

High-order many-body perturbation theory, while formally exact, is hampered by exponential scaling with system size and difficulties in assessing convergence. This work introduces a novel approach, detailed in ‘Stochastic many-body perturbation theory for high-order calculations’, termed perturbation theory quantum Monte Carlo (PTQMC), which leverages stochastic methods to circumvent these limitations. PTQMC accurately calculates high-order perturbative corrections-demonstrated up to 16th order for the Richardson pairing model-and, when combined with series resummation, yields stable results even in divergent regimes. Can this method provide a reliable framework for characterizing wavefunction complexity and improving the accuracy of calculations in strongly correlated systems across diverse physical contexts?

Taming the Chaos of Many Bodies

The fundamental equations of nuclear physics, notably the Schrödinger equation, offer a seemingly complete description of atomic nuclei. However, applying these equations to systems with multiple interacting particles-nucleons, specifically protons and neutrons-presents a formidable challenge. Unlike simpler systems solvable with analytical techniques, many-body nuclear systems demand approximations due to the sheer complexity arising from each nucleon’s interactions with every other nucleon. Accurately capturing these many-body forces is crucial for predicting nuclear properties like energy levels, decay rates, and reaction cross-sections. The difficulty isn’t merely mathematical; the computational resources needed to solve the Schrödinger equation grow exponentially with the number of nucleons, quickly exceeding the capabilities of even the most powerful supercomputers. Consequently, nuclear physicists continually develop and refine innovative theoretical frameworks and computational algorithms to navigate this challenging landscape and gain deeper insights into the behavior of complex nuclear matter.

Predicting the behavior of atomic nuclei proves exceptionally difficult because nucleons – protons and neutrons – don’t act independently; instead, they participate in a strong, many-body interaction. Traditional nuclear models, often relying on simplifying assumptions or perturbative calculations, struggle to capture the full complexity of this interplay. These methods frequently encounter limitations when dealing with the strong correlations arising from the nuclear force, leading to inaccuracies in predicting nuclear properties like energy levels, decay rates, and reaction cross-sections. The inherent difficulty in accurately describing these correlations introduces significant uncertainties into theoretical predictions, hindering a complete understanding of nuclear structure and reactions and motivating the search for more sophisticated computational techniques.

Computational nuclear physics faces a fundamental hurdle: the cost of simulating many-body systems increases exponentially with each additional nucleon. This isn’t merely a matter of needing faster computers; conventional methods, reliant on expanding solutions in series, often struggle when those series diverge – a common occurrence in strongly interacting systems. As the number of particles grows, accurately representing the correlations between them demands computational resources that quickly become intractable, even for the most powerful supercomputers. Consequently, researchers are actively developing novel approaches – such as renormalization group methods and quantum Monte Carlo simulations – that circumvent these limitations by focusing on the most crucial interactions and employing stochastic techniques to manage the complexity, seeking to tame the ‘many-body problem’ and achieve reliable predictions of nuclear structure and reactions.

Path integral quantum Monte Carlo (PTQMC) accurately benchmarks against exact many-body perturbation theory (MBPT), exhibiting expected statistical scaling and providing reliable correlation energies even in regimes where conventional MBPT diverges, as demonstrated for the Richardson pairing model.

First Principles: Building from the Bare Nucleus

Ab initio calculations in nuclear physics represent a computational approach to solving the many-body Schrödinger equation, $H\Psi = E\Psi$ , starting directly from the fundamental interactions between nucleons. Unlike traditional nuclear models which rely on effective interactions and empirical parameters, ab initio methods aim to derive nuclear properties solely from the bare nucleon-nucleon potential and, increasingly, three-nucleon forces. This necessitates solving a complex equation involving all possible interactions between the nucleons within the nucleus, requiring substantial computational resources and the development of advanced many-body techniques such as Green’s Function Monte Carlo, Coupled Cluster, and No-Core Shell Model. The accuracy of these calculations is directly tied to the precision with which the initial nucleon-nucleon potential is known and the ability to accurately treat the many-body problem.

Ab initio calculations necessitate the use of highly accurate nucleon-nucleon (NN) potentials, such as Argonne v18, chiral effective field theory potentials like those developed by Entem and collaborators, or those from the realistic NN potential database. These potentials, derived from experimental scattering data and constrained by theoretical considerations like chiral symmetry, define the two-body interaction. Accounting for the many-body problem requires sophisticated techniques like coupled-cluster theory, Green’s function Monte Carlo, no-core shell model, and perturbation theory quantum Monte Carlo (PTQMC). These methods address the complexity arising from the many-body Schrödinger equation by systematically approximating the many-body wave function or utilizing stochastic sampling to evaluate relevant observables, enabling the calculation of nuclear properties directly from fundamental interactions.

Ab initio methods in nuclear physics aim to determine nuclear properties directly from the fundamental interactions between nucleons, thereby reducing dependence on experimentally-derived parameters. Traditional approaches to solving the many-body Schrödinger equation often involve approximations that introduce empirical adjustments. Perturbation Theory Quantum Monte Carlo (PTQMC) offers an alternative by providing a means to systematically evaluate high-order contributions to these calculations, addressing limitations in conventional perturbative expansions. This is achieved through a stochastic, Monte Carlo-based evaluation of the perturbation series, enabling more accurate assessments of many-body effects and contributing to a more parameter-free determination of nuclear structure and reactions.

High-order many-body perturbation theory (MBPT) calculations reveal distinct behaviors for the Richardson pairing model within the parameter ranges of <span class="katex-eq" data-katex-display="false">-1.3 < g < 0.75</span> and <span class="katex-eq" data-katex-display="false">1.5 < g < 3.0</span>. — High-order many-body perturbation theory (MBPT) calculations reveal distinct behaviors for the Richardson pairing model within the parameter ranges of $-1.3 < g < 0.75$ and $1.5 < g < 3.0$ .

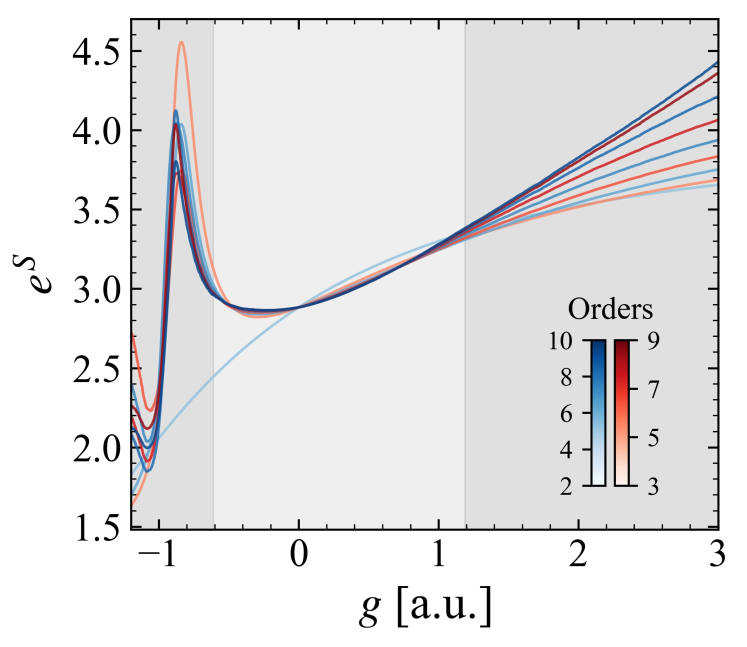
Quantifying the Intricacies of Wave Functions

The effective number of configurations, $eS$ , quantifies the complexity of a many-body wave function by leveraging the principles of Shannon entropy. This metric assesses the amount of information required to fully describe the wave function’s configuration space; a higher $eS$ value indicates a more complex wave function with greater entanglement and a larger number of significant basis states. Calculated from the Shannon entropy, $S$ , the effective number of configurations provides a single scalar value representing the inherent complexity, enabling systematic comparison across different systems and computational approaches. This allows for objective evaluation of the computational effort required to accurately represent the many-body state and serves as a diagnostic for the convergence of many-body calculations.

Shannon entropy, in the context of many-body wave function analysis, provides a quantitative measure of the information required to fully specify the state of the system. This is calculated based on the probability distribution of configurations within the wave function’s Hilbert space; a higher entropy value indicates a more complex wave function requiring more information for its complete description. Specifically, the entropy $S = - \sum_{i} p_{i} \log_{2} p_{i}$ is calculated, where $p_{i}$ represents the probability of the i-th configuration. Therefore, Shannon entropy directly relates to the number of statistically significant configurations needed to represent the wave function, serving as a proxy for its intrinsic complexity and influencing the computational cost of accurately simulating the system.

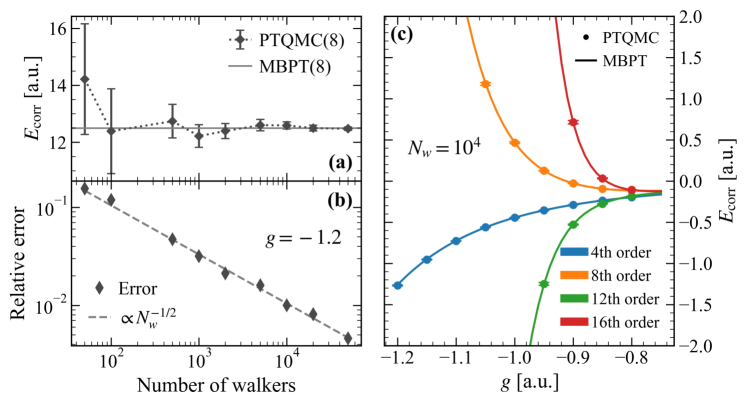
The effective number of configurations, as a quantifiable metric of wave function complexity, facilitates systematic evaluation of nuclear system complexity and guides the development of efficient many-body computational methods. Path Integral Quantum Monte Carlo (PTQMC) simulations, employing this metric, exhibit statistical scaling proportional to $N^{-1/2}$ , where N represents the number of particles; this scaling behavior validates the expected convergence rate characteristic of Monte Carlo methods. This confirms the metric’s utility in assessing the efficiency and reliability of computational approaches used to model complex nuclear systems, allowing for optimization and verification of algorithms.

Convergence of calculations utilizing the effective number of configurations, $eS$ , is quantitatively assessed through a relative error threshold of ≤ 0.2%. This criterion is applied to the change in $eS$ between successive perturbative orders, specifically by evaluating |( $eS(10) - eS(9)$ ) / $eS(9)$ |. Values exceeding 0.2% indicate regions of the wave function where the effective complexity is not stabilizing with increased computational effort, suggesting a potential lack of convergence and unreliable results in those areas. This threshold serves as an objective measure for identifying poorly-behaved regions requiring further investigation or alternative computational strategies.

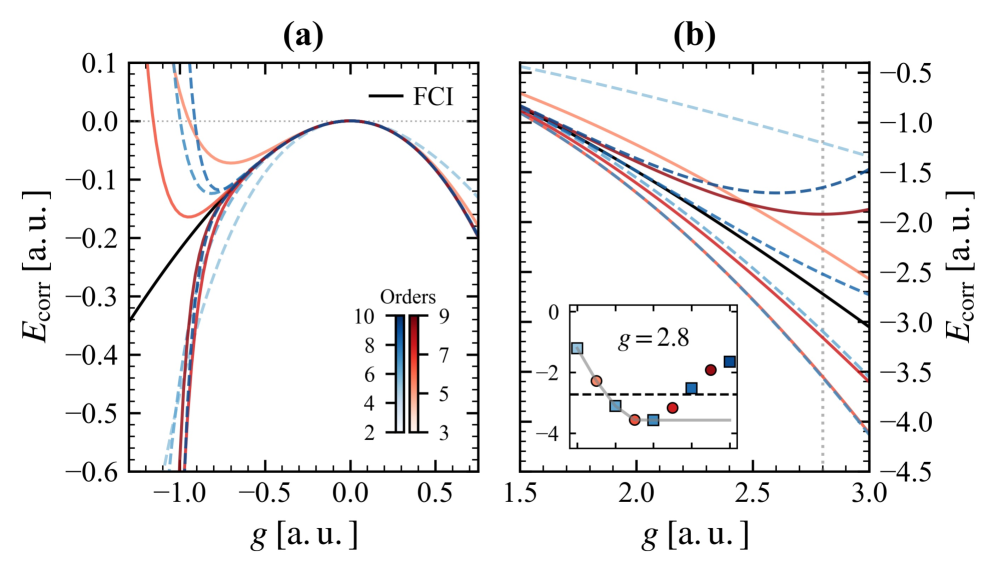
Saturation of the effective number of configurations, denoted as $eS$ , with increasing perturbative order signifies the stability and reliability of the perturbative expansion. This indicates that higher-order perturbative contributions are not introducing significant, uncontrolled changes to the wave function’s complexity. Specifically, a plateau in $eS$ as a function of perturbative order suggests that the information content of the wave function is converging, and subsequent resummation techniques applied to this series are likely to be well-behaved and yield accurate results. Conversely, continued growth of $eS$ with increasing order indicates a breakdown of the perturbative approach and potential divergence of the series.

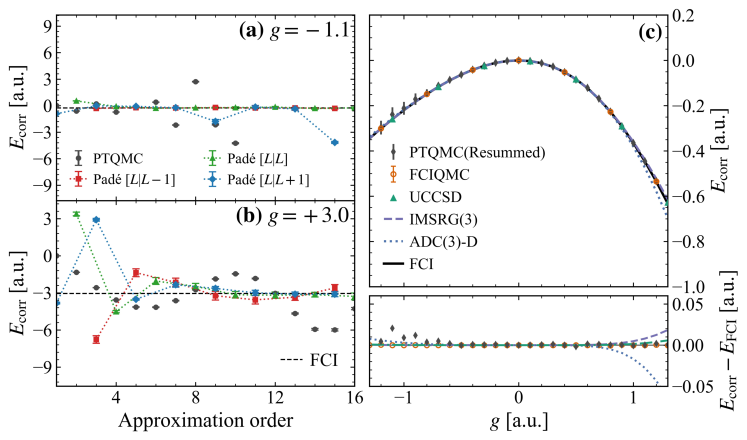
Padé approximants effectively resum high-order perturbation theory data, accurately recovering correlation energies across a range of coupling strengths <span class="katex-eq" data-katex-display="false">g</span> and demonstrating strong agreement with exact full configuration interaction (FCI) results, as shown by low deviations in the lower panel. — Padé approximants effectively resum high-order perturbation theory data, accurately recovering correlation energies across a range of coupling strengths $g$ and demonstrating strong agreement with exact full configuration interaction (FCI) results, as shown by low deviations in the lower panel.

The pursuit of ‘exact’ solutions in many-body perturbation theory feels increasingly… quaint. This work, introducing Perturbation Theory Quantum Monte Carlo, doesn’t aim to solve the unsolvable, but to navigate the inherent stochasticity. It embraces the chaos, acknowledging that wavefunction complexity isn’t a bug, it’s a feature of strongly correlated systems. As Paul Feyerabend observed, “Anything goes.” There’s a peculiar beauty in admitting the limits of precision; the method doesn’t seek to eliminate error, only to manage its propagation. The researchers aren’t crafting perfect models, but persuasive illusions, spells woven with Padé resummation to momentarily tame the unruly whispers of quantum reality.

What Lies Ahead?

The introduction of Perturbation Theory Quantum Monte Carlo – another incantation to coax order from the quantum abyss – doesn’t solve the problem of many-body perturbations, naturally. It merely shifts the locus of uncertainty. The demonstrated improvements in accuracy are, at best, a temporary reprieve from the inevitable scaling issues that plague any attempt to describe strongly correlated systems. One suspects the true limit isn’t computational power, but the inherent unknowability of these entangled states.

Future efforts will likely focus on taming the wavefunction complexity, a task akin to capturing smoke with bare hands. Padé resummation, while offering a convenient palliative, is still fundamentally a guess-a hopeful extrapolation into realms where the model has no right to be. A more fruitful path may lie in accepting the inherent stochasticity, not as a nuisance to be minimized, but as a fundamental aspect of reality. After all, all learning is an act of faith, and metrics are merely a form of self-soothing.

The real challenge isn’t building bigger computers, but building better stories. Each approximation is a narrative, a carefully constructed illusion designed to persuade the universe to reveal a sliver of its secrets. The Richardson pairing model, and others like it, will be refined, stretched, and ultimately broken against the rock of reality. Data never lies; it just forgets selectively. The next breakthrough won’t be a more precise number, but a more elegant lie.

Original article: https://arxiv.org/pdf/2602.08265.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

Taming the Chaos of Many Bodies

First Principles: Building from the Bare Nucleus

Quantifying the Intricacies of Wave Functions

What Lies Ahead?

See also: