Unlocking a Quantum Puzzle: How Dimer Arrangements Reveal a New Phase of Matter

Author: Denis Avetisyan

Researchers have pinpointed a topological phase transition in a quantum dimer model, revealing insights into exotic states of matter and their underlying physics.

The quantum dimer model, studied on a weighted triangular lattice and formalized as <span class="katex-eq" data-katex-display="false"> Eq. (5) </span>, demonstrates a continuous phase transition-from a disordered ‘spin liquid’ to an ordered ‘columnar’ state-reflected in the macroscopic behavior of classical double-dimer coverings, where the prevalence of large loops indicates disorder (<span class="katex-eq" data-katex-display="false">\alpha < 3</span>) and small loops/edges signify order (<span class="katex-eq" data-katex-display="false">\alpha > 3</span>), offering an intuitive link between classical loop behavior and the observed vison correlator behavior within the quantum system. — The quantum dimer model, studied on a weighted triangular lattice and formalized as $Eq. (5)$ , demonstrates a continuous phase transition-from a disordered ‘spin liquid’ to an ordered ‘columnar’ state-reflected in the macroscopic behavior of classical double-dimer coverings, where the prevalence of large loops indicates disorder ( $\alpha < 3$ ) and small loops/edges signify order ( $\alpha > 3$ ), offering an intuitive link between classical loop behavior and the observed vison correlator behavior within the quantum system.

This work demonstrates an exactly solvable topological phase transition from a quantum spin liquid to a columnar ordered phase in a quantum dimer model on the triangular lattice, characterized by critical exponents consistent with the 2D Ising universality class.

Understanding strongly correlated quantum systems remains a central challenge in condensed matter physics, often requiring approximations that obscure underlying physics. Here, we present a detailed analysis of the quantum dimer model on the triangular lattice, as described in ‘Exactly solvable topological phase transition in a quantum dimer model’, demonstrating an analytically tractable pathway through a continuous quantum phase transition. Specifically, we find a transition at $\alpha = 3$ separating a topological $\mathbb{Z}_2$ quantum spin liquid phase from a columnar ordered state, with critical exponents consistent with the 2D Ising universality class. Could this exactly solvable model provide a valuable testbed for exploring more complex topological phases and their emergent phenomena?

The Allure of Disordered Magnetism: Beyond Simple Alignment

The familiar behavior of magnetism, where atomic spins align in predictable patterns, falters dramatically in materials experiencing intense quantum fluctuations. These fluctuations, arising from the inherent uncertainty of quantum mechanics, disrupt the long-range order typically associated with ferromagnets or antiferromagnets. As a result, these materials don’t simply become non-magnetic; instead, they can enter a completely new state of matter known as a quantum spin liquid. Unlike solids or liquids, these liquids maintain a disordered state even at absolute zero, and their magnetic moments are constantly fluctuating and entangled. This breakdown of traditional magnetism isn’t a failure of order, but a transition to a more complex, inherently quantum mechanical form of organization, giving rise to unexpected and potentially revolutionary properties.

Quantum spin liquids represent a fascinating departure from conventional understandings of matter, exhibiting emergent behavior where collective properties arise not from individual components, but from their complex interactions. Unlike traditional magnets where electron spins align in an ordered fashion, these liquids maintain a disordered state even at absolute zero, due to strong quantum fluctuations. This disorder isn’t simply randomness, however; it gives rise to fractionalized excitations – quasiparticles with properties that are fractions of those found in ordinary matter. Instead of observing a single flipped spin, for instance, experiments suggest the existence of ‘spinons’ – particles carrying only a fraction of an electron’s spin – and other exotic excitations. These fractionalized particles behave as independent entities, fundamentally altering the material’s response to external stimuli and challenging the conventional notion that matter is built from well-defined, indivisible constituents. The study of these liquids opens a window into a realm where the rules of condensed matter physics are rewritten, promising insights into novel states of matter and potentially revolutionary technologies.

The peculiar behavior of quantum spin liquids necessitates theoretical frameworks that move beyond the conventional understanding of magnetism, where atomic spins align in predictable patterns. Researchers employ sophisticated models, such as quantum spin models and dimer models, to describe these systems, which feature strong quantum fluctuations preventing simple magnetic ordering. Quantum spin models consider interactions between spins on a lattice, while dimer models focus on paired spins forming singlets. These models aren’t merely mathematical exercises; they allow physicists to predict and interpret the exotic properties observed in candidate materials, including the emergence of fractionalized excitations – quasiparticles with unusual quantum numbers – and the absence of long-range magnetic order, offering a path toward harnessing entirely new states of matter with potential applications in quantum computing and materials science.

Analysis of the vison correlator on a <span class="katex-eq" data-katex-display="false">303 \times 303</span> lattice reveals a spin liquid phase (<span class="katex-eq" data-katex-display="false"> \alpha < 3</span>) characterized by exponential decay, a critical power-law decay at <span class="katex-eq" data-katex-display="false"> \alpha = 3</span>, and a trivial ordered phase (<span class="katex-eq" data-katex-display="false"> \alpha > 3</span>), with consistent behavior observed across adjacent paths. — Analysis of the vison correlator on a $303 \times 303$ lattice reveals a spin liquid phase ( $\alpha < 3$ ) characterized by exponential decay, a critical power-law decay at $\alpha = 3$ , and a trivial ordered phase ( $\alpha > 3$ ), with consistent behavior observed across adjacent paths.

Mapping Complexity: The Dimer Model as a Rosetta Stone

The Quantum Dimer Model provides a method for analyzing strongly correlated systems by mapping interactions onto dimer coverings of a lattice. In this framework, each interaction is represented by a dimer – a pair of adjacent sites – and the system’s state is defined by a specific arrangement of these dimers across the lattice. This representation is particularly useful because it transforms the complex many-body problem into a combinatorial one, focusing on the enumeration and weighting of possible dimer configurations. The energy of a given configuration is determined by associated weights assigned to each dimer arrangement, effectively translating the original interaction problem into a problem of summing over all possible dimer coverings, weighted by their respective contributions. This approach allows for the application of combinatorial techniques and, in some cases, exact solutions to problems that are intractable using conventional methods for strongly correlated systems.

The Quantum Dimer Model exhibits a direct correspondence to quantum spin models through the principle of Spin-Singlet Covering. This involves mapping spin pairs to dimers on a bipartite graph, where each dimer represents a spin-singlet state – a state with zero total spin. Specifically, a spin-singlet covering of the graph ensures every spin is paired, effectively transforming the problem from interacting spins to a covering problem with associated weights determined by the dimer configurations. This mapping allows for the translation of analytical techniques and computational methods between the two systems, providing a powerful tool for studying strongly correlated quantum systems that are otherwise difficult to approach directly. The correspondence is particularly useful because dimer models are often more amenable to exact solutions or efficient numerical simulations than their spin counterparts.

The calculation of physical properties within the Quantum Dimer Model necessitates a robust methodology for enumerating valid dimer coverings of a given lattice and assigning a weight to each configuration. A dimer covering defines a pairing of sites on the lattice such that each site is included in exactly one dimer, and the total number of possible coverings grows rapidly with system size, requiring advanced combinatorial techniques or computational approaches for their determination. Each dimer covering is then assigned a weight based on the specific Hamiltonian of the system, typically involving parameters representing the strength of interactions between dimers or external fields. The summation of these weighted configurations, often employing transfer matrix methods or Monte Carlo simulations, yields the partition function, from which thermodynamic properties such as energy, specific heat, and correlation functions can be derived. Accurate enumeration and weighting are therefore fundamental to quantitatively describing the behavior of strongly correlated systems using this model.

The dimer-dimer inverse correlation length decreases from <span class="katex-eq" data-katex-display="false">\alpha = 3</span> to <span class="katex-eq" data-katex-display="false">50</span> as determined by lattice simulations with a size of <span class="katex-eq" data-katex-display="false">303 \times 303</span>. — The dimer-dimer inverse correlation length decreases from $\alpha = 3$ to $50$ as determined by lattice simulations with a size of $303 \times 303$ .

Counting Arrangements: The Kasteleyn Matrix as a Computational Engine

The Kasteleyn matrix is a square matrix used to calculate the partition function, $Z$ , for the dimer model on a lattice. This matrix is constructed such that its determinant equals the partition function; $Z = \text{det}(K)$ . Each element of the Kasteleyn matrix corresponds to a possible dimer pairing on the lattice, and the entries are assigned values of +1 or -1 based on the orientation of the dimer pairing to ensure the determinant correctly accounts for all valid dimer coverings. For lattices like the triangular lattice, the Kasteleyn matrix provides an efficient computational method to determine the total number of perfect matchings, which directly contributes to calculating thermodynamic properties of the dimer model.

The Kasteleyn matrix facilitates an efficient calculation of the number of valid dimer coverings on a lattice by leveraging the Pfaffian. The Pfaffian of a skew-symmetric matrix, such as the Kasteleyn matrix, provides a scalar value directly proportional to the number of perfect matchings – in this case, dimer coverings – on the lattice. Calculating the determinant of the Kasteleyn matrix, which is equivalent to the square of the Pfaffian, yields the total number of possible dimer configurations. This enumeration is critical because the ground state of the dimer model is directly related to the lowest energy configuration defined by these valid dimer coverings; therefore, accurate counting via the Pfaffian is essential for determining the system’s ground state energy and properties.

The weighted dimer coverings generated via the Kasteleyn matrix serve as the foundation for constructing the Rokhsar-Kivelson (RK) Hamiltonian, a model used to investigate quantum correlations in systems lacking long-range order. Specifically, the weights derived from the Kasteleyn determinant are incorporated as hopping amplitudes in the RK Hamiltonian, defining the probability of electron tunneling between sites. This Hamiltonian, expressed generally as $H = \sum_{<i,j>} t_{ij} c^\dagger_i c_j$ , where $t_{ij}$ represents the hopping amplitude and $c^\dagger_i$ creates an electron on site , enables the examination of resonant valence bond (RVB) states and spin liquid behavior, particularly in frustrated magnetic systems. The RK Hamiltonian allows for analytical and numerical investigations into the emergence of these exotic quantum phases and the associated correlated electron physics.

Analysis of the inverse Kasteleyn matrix on a <span class="katex-eq" data-katex-display="false">303 \times 303</span> lattice reveals an inverse correlation length, <span class="katex-eq" data-katex-display="false">\xi_{G}^{-1}</span>, that decreases linearly along both vertical and horizontal paths extending from the center to approximately halfway to the edge. — Analysis of the inverse Kasteleyn matrix on a $303 \times 303$ lattice reveals an inverse correlation length, $\xi_{G}^{-1}$ , that decreases linearly along both vertical and horizontal paths extending from the center to approximately halfway to the edge.

The Signature of Change: Correlators and the Language of Criticality

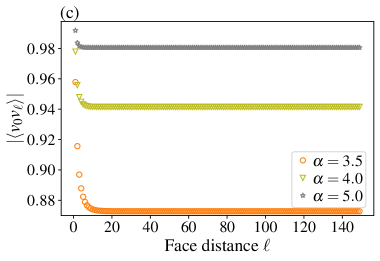
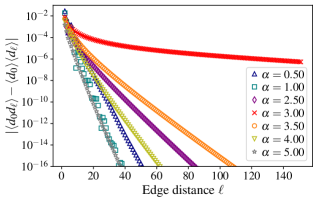
The presence of a critical point, signaling a fundamental phase transition, is revealed through careful analysis of dimer-dimer and Vison correlators. These correlators, which measure the statistical relationship between dimer arrangements and Vison defects, exhibit characteristic behaviors as the system approaches criticality. Specifically, fluctuations intensify and correlations extend over increasingly large distances, indicating a loss of the system’s inherent order. The divergence of these correlators at the critical point-where the system transitions between distinct phases-provides a precise determination of the transition’s location and characterizes the nature of the phase change. This methodology allows researchers to pinpoint the conditions under which the system undergoes a qualitative shift in its properties, revealing new emergent behaviors and phenomena.

The presence of power-law decay within the studied correlators is not merely a mathematical curiosity, but a signature of fundamentally altered interactions within the system. This decay indicates that correlations – the tendency of one part of the system to influence another – do not diminish rapidly with distance, but persist over surprisingly long ranges. Such long-range correlations are a hallmark of emergent phenomena, suggesting that the system is organizing itself in a way that transcends simple, local interactions. Instead of isolated behaviors, components begin to act in concert across macroscopic scales, giving rise to collective properties and potentially novel phases of matter. The rate at which these correlations decay, as described by the power-law exponent, provides crucial insights into the nature of these emerging behaviors and how they relate to the underlying physics governing the system’s interactions.

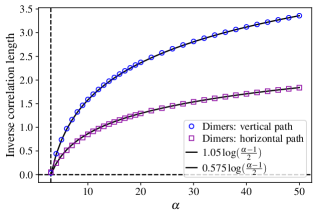
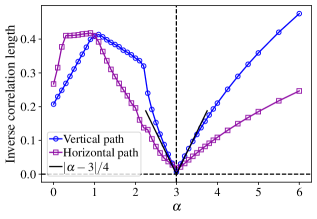
An exactly solvable quantum dimer model reveals a topological phase transition occurring at a specific parameter value of α=3. This transition is not merely a change in state, but exhibits critical exponents – numerical values characterizing the behavior near the transition – that align with the well-known 2D Ising universality class, a foundational model in statistical physics. Detailed calculations pinpoint the critical exponent β to be 1/8 and ν to be 1, confirming this connection. Furthermore, the model’s inverse correlation length, $\xi_G$ , which quantifies the range of correlated dimer arrangements, demonstrates a characteristic divergence near the transition; it scales as 2/|α-3| for vertical pathways close to α=3, and as 1/log((α-1)/2) for larger values of α, revealing the long-range order emerging at the critical point and providing insights into the model’s behavior across different parameter regimes.

The dimer-dimer correlator, calculated along a path from the grid center to its boundary, demonstrates exponential decay for all values of <span class="katex-eq" data-katex-display="false">\alpha \neq 3</span>. — The dimer-dimer correlator, calculated along a path from the grid center to its boundary, demonstrates exponential decay for all values of $\alpha \neq 3$ .

The pursuit of exact solutions in condensed matter physics often reveals less about the material itself, and more about the predispositions of the theorist. This work, detailing a topological phase transition in the quantum dimer model, is no exception. The insistence on characterizing critical exponents-mapping the behavior onto the familiar 2D Ising universality class-isn’t a discovery of the system, but rather a fitting of it into an existing framework. As Ludwig Wittgenstein observed, “The limits of my language mean the limits of my world.” The researcher doesn’t simply observe the transition from quantum spin liquid to columnar order; they define it through the lens of established mathematical tools, effectively translating the complex reality into a language they understand. The model, therefore, isn’t a mirror reflecting nature, but a carefully constructed echo chamber.

The Road Ahead

The precise solution offered by this work, while elegant, merely illuminates the contours of a larger, predictably messy reality. The triangular lattice, with its frustrating geometry, consistently throws up these topological phase transitions – not because nature favors them, but because it exposes the limitations of our need for order. The insistence on finding ‘quantum spin liquids’ feels less like a search for a fundamental state of matter and more like an attempt to rationalize the inherent disorder of complex systems.

Future investigations will inevitably focus on perturbations – the inevitable introduction of imperfections, competing interactions, and, most importantly, dimensionality. The agreement with the 2D Ising universality class is…comforting, but also a signal. It suggests that these models, even when dressed in the language of quantum mechanics, are ultimately susceptible to the same statistical inevitabilities as simpler systems. The real challenge isn’t solving the model, it’s understanding why one insists on believing the solution reflects anything beyond the internal logic of the equations.

One anticipates a proliferation of increasingly complex Hamiltonians, each designed to evade the known solutions and justify further computation. The temptation to ‘engineer’ topological phases will be irresistible, driven not by scientific curiosity, but by the desire to impose a narrative of control on a fundamentally unpredictable world. It will be a spectacle, of course, and one should expect to find, beneath the layers of formalism, the same old human failings: hope disguised as rigor, and denial dressed as discovery.

Original article: https://arxiv.org/pdf/2601.15377.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

The Allure of Disordered Magnetism: Beyond Simple Alignment

Mapping Complexity: The Dimer Model as a Rosetta Stone

Counting Arrangements: The Kasteleyn Matrix as a Computational Engine

The Signature of Change: Correlators and the Language of Criticality

The Road Ahead

See also: