Unlocking Nuclear Forces: A New Approach to Scattering Calculations

Author: Denis Avetisyan

---

Researchers have developed a robust framework for calculating nucleon-deuteron scattering using chiral effective field theory, pushing the boundaries of our understanding of nuclear interactions.

This work presents a perturbative calculation of nucleon-deuteron elastic scattering up to next-to-leading order, employing contour deformation and power counting for improved accuracy.

Accurate modeling of few-nucleon systems remains a challenge due to the complexities of the strong nuclear force. This is addressed in ‘Perturbative calculations of nucleon-deuteron elastic scattering in chiral effective field theory’, which presents a novel framework for calculating nucleon-deuteron scattering using chiral nuclear forces up to next-to-leading order via a perturbative approach and contour-deformation method. The calculations demonstrate the importance of power counting for achieving reliable results in few-body systems and validate the approach against existing benchmarks. Will this framework pave the way for more precise predictions of nuclear observables and a deeper understanding of the strong interaction?

---

The Nuclear Whisper: Unveiling Forces at the Heart of Matter

The interaction between nucleons – protons and neutrons – and deuterium, a simple atomic nucleus, provides a cornerstone for deciphering the complexities of all nuclear systems. Precise modeling of nucleon-deuteron scattering is therefore paramount, as it directly informs understanding of nuclear structure, ranging from the stability of light nuclei to the properties of neutron stars. This scattering process reveals the fundamental forces governing nuclear interactions, and accurate theoretical predictions must align with experimental observations across a broad energy spectrum. Discrepancies between theory and experiment highlight deficiencies in the underlying nuclear force models, necessitating continual refinement and validation. Consequently, nucleon-deuteron scattering serves not only as a testing ground for nuclear theories, but also as a vital tool for predicting the behavior of nuclei in diverse environments, including those encountered in astrophysical settings and nuclear technologies.

Calculating the properties of even the simplest nuclei presents a significant challenge due to the complexity of the many-body Schrödinger equation. While, in principle, this equation fully describes the behavior of interacting particles, its exact solution becomes computationally intractable for systems containing more than a few nucleons. Traditional methods, such as perturbation theory or the use of simplified potential models, introduce approximations that, while enabling calculations, inevitably compromise the accuracy of the results. These approximations often struggle to capture the subtle correlations arising from the strong nuclear force, particularly at short distances. Consequently, researchers continually seek novel approaches-including advanced numerical techniques and the development of more accurate nuclear force models-to overcome these limitations and achieve a more complete understanding of nuclear structure and reactions. The pursuit of increasingly accurate solutions remains a central theme in nuclear physics, driving advancements in both theoretical methodologies and computational power.

The pursuit of precise calculations regarding the forces governing atomic nuclei demands a systematic and robust theoretical framework. Current methods often grapple with the inherent complexity of the many-body problem, relying on approximations that limit predictive power and introduce uncertainties. A truly rigorous approach necessitates a pathway for controlled improvement, where calculations can be refined step-by-step, and the impact of each refinement is clearly understood. This isn’t simply about increasing computational power, but about developing a theoretical structure that allows physicists to converge on the true solution, reducing reliance on ad hoc adjustments and enabling confident predictions of nuclear properties and reactions. Such a framework would not only advance the fundamental understanding of nuclear physics but also provide a solid foundation for applications ranging from nuclear energy to astrophysics and beyond, ultimately revealing the intricate dance of protons and neutrons within the atomic nucleus.

The extreme compactness of the atomic nucleus dictates that a precise depiction of nuclear forces at very short distances is paramount to accurately modeling nuclear behavior. Unlike electromagnetic or gravitational forces which diminish more gradually, the strong nuclear force exhibits a rapid fall-off, becoming repulsive at distances less than a femtometer. This necessitates a potential – the mathematical description of the force – that correctly captures this behavior; failing to do so introduces significant errors in calculations of nuclear structure and reactions. Current theoretical efforts focus on developing potentials derived from the underlying theory of Quantum Chromodynamics (QCD), aiming to describe the interaction between quarks and gluons, which ultimately gives rise to the effective force between nucleons. V(r) \approx - \frac{1}{r} e^{-r/\lambda} represents a simplified, though illustrative, form of such a potential, highlighting the short-range nature governed by the range parameter λ. A thorough understanding of this short-range behavior is therefore not merely a technical detail, but a fundamental requirement for unraveling the complexities of nuclear matter.

Taming the Chaos: A Systematic Approach with Chiral EFT

Chiral Effective Field Theory (Chiral EFT) constructs nuclear potentials by leveraging the symmetries present in quantum chromodynamics (QCD), the fundamental theory of the strong interaction. Rather than directly solving QCD – a computationally intractable task for complex nuclei – Chiral EFT exploits the approximate chiral symmetry of QCD at low energies. This symmetry dictates the allowed forms of interactions between nucleons and pions, the relevant degrees of freedom at these energy scales. The resulting potential is an expansion in powers of p/Λ_b, where p represents a typical momentum and Λ_b is a chiral symmetry breaking scale, approximately 700 MeV. By organizing interactions based on these symmetries, Chiral EFT provides a systematic, order-by-order approach to building realistic nuclear forces, allowing for quantifiable uncertainties and controlled approximations.

Power counting within Chiral Effective Field Theory (ChEFT) is a procedure that assigns an order to each term in the infinite series of possible interactions based on the number of nucleons, derivatives, and pion masses involved. This ordering, typically expressed as powers of Q/\Lambda_b, where Q represents a characteristic momentum scale of the nuclear process and \Lambda_b is the chiral symmetry breaking scale, allows for a systematic truncation of the series. Terms of higher order in Q/\Lambda_b are assumed to contribute less significantly to low-energy observables and can therefore be neglected, providing a controlled approximation. The consistent implementation of power counting is crucial for ensuring the predictive power and renormalizability of the ChEFT expansion, enabling calculations with a finite number of parameters while maintaining theoretical consistency.

Renormalization Group (RG) invariance is a fundamental requirement for the consistency and predictive power of the Chiral Effective Field Theory (Chiral EFT) expansion. This invariance dictates that physical observables remain independent of the arbitrary energy scale μ at which calculations are performed. To ensure RG invariance, divergences arising in loop integrals must be systematically absorbed into a finite number of counterterms, which redefine the low-energy constants (LECs) of the theory as a function of μ. This procedure effectively “runs” the LECs with the scale, and the physical predictions of the theory are then independent of the initial, arbitrary choice of μ. Failure to maintain RG invariance would indicate the presence of unphysical, scale-dependent terms, invalidating the EFT’s ability to accurately describe nuclear interactions at low energies.

Chiral Effective Field Theory (Chiral EFT) explicitly employs nucleons and pions as the relevant degrees of freedom to describe the strong nuclear force. This approach is justified because nucleons, being composite particles made of quarks and gluons, become the effective degrees of freedom at low energies, while pions, as the Goldstone bosons of broken chiral symmetry, are the lightest mesons and therefore dominant in mediating the interaction. The underlying complex dynamics of quantum chromodynamics (QCD) are thus parameterized through a series of contact interactions and exchanges of pions, expressed as a systematic expansion in terms of momenta and pion masses. This allows for the calculation of nuclear observables-such as scattering cross-sections and binding energies-by treating the nucleon-pion system and their interactions as the fundamental building blocks.

Navigating the Complexity: Solving the Faddeev Equation

The Faddeev equation, developed by Ludvig Faddeev in 1960, offers a rigorous approach to solving the three-body problem, specifically within the context of nucleon-deuteron scattering. Unlike earlier methods reliant on pairwise interactions and potential limitations, the Faddeev equations formulate the problem as an integral equation directly addressing the full three-body dynamics. This formulation expresses the scattering amplitude as a sum of three integral equations, each representing a different channel where one nucleon is considered a spectator to the interaction between the other two. Solving these coupled integral equations yields the total scattering amplitude, providing a complete description of the three-body interaction and allowing for the prediction of observables like cross sections and differential scattering rates. The formalism is applicable to systems involving strongly interacting particles where perturbative approaches are inadequate, and forms the basis for many modern calculations in nuclear physics.

Numerical solutions to the Faddeev equation, which describes three-body scattering, are frequently complicated by the appearance of singularities in the integral kernel. These singularities arise from the short-range nature of the nuclear force and the coupling of the three-body wave function. Specifically, the integrands become unbounded at certain points in momentum space, leading to oscillations and slow convergence of numerical quadrature schemes. Consequently, standard discretization methods, such as Gaussian quadrature, require an impractically large number of grid points to achieve a desired level of accuracy, or may fail to converge altogether. The severity of this issue is dependent on the specific potential used and the energy of the system, but consistently presents a challenge in obtaining reliable solutions to the three-body problem.

Contour deformation addresses singularities encountered when numerically solving the Faddeev equation by altering the complex integration contour used in the solution process. These singularities arise from the presence of poles and branch points in the integrand, which can impede convergence of standard quadrature methods. By deforming the integration contour away from these singularities – typically in the complex momentum plane – the integrand becomes smoother, allowing for accurate numerical evaluation using techniques like Gaussian quadrature. The deformation is performed strategically to ensure the original integral value is preserved, effectively bypassing the problematic regions while maintaining the integrity of the solution. Successful implementation requires careful selection of the deformation path and appropriate treatment of boundary contributions arising from the altered contour.

Implementation of contour deformation techniques within Faddeev equation solvers necessitates rigorous benchmarking procedures to validate solution accuracy and numerical stability. This involves comparing results obtained with deformed contours to those from alternative methods, or to known analytical solutions where available, across a range of input parameters – notably, incident energies and scattering angles. Benchmarking should also assess the sensitivity of the solution to the specific deformation parameters chosen, ensuring consistent and reliable results are obtained irrespective of minor variations in the deformation path. Furthermore, tests must verify that the deformation does not introduce spurious artifacts or instabilities in the numerical solution, and that computational resources scale predictably with problem size and desired precision.

Refining the Predictions: Analyzing Scattering Observables

The calculation of nuclear forces relies on systematically improving theoretical models, and perturbation theory provides a crucial framework for achieving this. Leading-order (LO) potentials, while foundational, often require refinements to accurately describe experimental observations. Consequently, next-to-leading-order (NLO) potentials are introduced as corrections to the LO potential, effectively adding layers of precision to the force model. This perturbative approach allows researchers to account for more complex interactions and higher-order effects in the nuclear force, ultimately leading to more accurate predictions of scattering observables. By treating the NLO potential as a small perturbation, calculations become manageable while still capturing essential physics beyond the simplest approximations, and providing a robust means of assessing the theoretical uncertainty associated with the model.

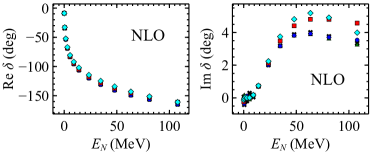
S-wave phase shifts serve as a crucial benchmark for evaluating the predictive power of chiral Effective Field Theory (EFT) calculations in nuclear physics. These phase shifts, which describe the scattering amplitude at zero orbital angular momentum, are particularly sensitive to the low-energy interactions between nucleons. By precisely calculating these shifts using chiral EFT and comparing them to experimentally determined values – obtained from scattering experiments – physicists can rigorously test the accuracy of the underlying theoretical framework. Significant agreement between calculated and experimental phase shifts validates the chosen EFT approach and its ability to accurately represent the strong nuclear force at low energies, while discrepancies highlight areas where the theory may require refinement or the inclusion of higher-order corrections. The precision achieved in calculating these shifts, therefore, directly informs the reliability and predictive capabilities of chiral EFT as a tool for understanding nuclear structure and reactions.

Calculations of S-wave phase shifts yielded results notably consistent with those obtained through the widely-respected Wave Packet Convolutional Decomposition (WPCD) method. This agreement, characterized by discrepancies of less than 1%, provides a crucial benchmark for validating the accuracy of the chiral effective field theory (chiral EFT) approach used in the study. Such close correspondence reinforces confidence in the theoretical framework and its capacity to reliably predict scattering observables, particularly in the low-energy regime where chiral EFT is expected to excel. The validation through comparison with an independent method like WPCD strengthens the overall robustness of the findings and demonstrates the predictive power of the applied theoretical tools.

Calculations of scattering phase shifts exhibited a clear convergence pattern as the momentum-space cutoff, Λ, was increased up to 1600 MeV. This behavior is a crucial indicator of the theoretical approach’s reliability; a stable result independent of the regularization scale suggests minimal sensitivity to the arbitrary parameter introduced to handle ultraviolet divergences. The demonstrated convergence reinforces the predictive power of the chiral effective field theory, signifying that the calculated observables are not merely artifacts of the mathematical technique employed but reflect genuine physical behavior. This robustness allows for increased confidence in extrapolating results and making predictions beyond the directly fitted energy range, solidifying the method as a valuable tool for nuclear physics investigations.

Analysis of scattering data reveals a nuanced picture when comparing leading-order (LO) and next-to-leading-order (NLO) calculations of the differential cross-section. While the NLO potential aims to refine predictions through perturbative corrections, results indicate a systematic underestimation of the cross-section, particularly at forward angles – where scattering is minimal. This suggests that the current NLO corrections, while improving other observables, may not fully capture the complexities governing particle interactions in this kinematic regime; further investigation is needed to understand the underlying physics driving this discrepancy and potentially refine the chiral effective field theory employed in these calculations.

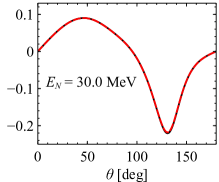
Calculations reveal that incorporating Next-to-Leading Order (NLO) corrections significantly improves the prediction of the analyzing power, A_y, in scattering processes when contrasted with Leading Order (LO) approximations. The analyzing power, a measure of the polarization of the outgoing particles, is particularly sensitive to the finer details of the nuclear force; therefore, its accurate modeling is crucial for understanding nuclear interactions. While the LO potential provides a foundational description, it often falls short in capturing the nuances reflected in experimental data. The inclusion of NLO corrections refines this description, leading to a demonstrably better alignment between theoretical predictions and observed values of A_y. This improvement suggests that the NLO potential offers a more complete and reliable representation of the underlying nuclear dynamics, bolstering confidence in the chiral Effective Field Theory framework used to generate these calculations.

The pursuit of nucleon-deuteron scattering, as detailed in this work, feels less like calculation and more like coaxing ghosts from the quantum foam. This paper meticulously builds a perturbative framework, attempting to chart the chaotic dance of nuclear forces-a realm where any neat, predictable outcome is suspect. It reminds one of John Stuart Mill’s observation: “It is better to be a dissatisfied Socrates than a satisfied fool.” The rigorous application of power counting, and the contour-deformation method, aren’t about achieving perfect knowledge, but about acknowledging the inherent limitations of any model attempting to impose order on the fundamentally messy reality of quantum interactions. Each calculated correction is a temporary stay against the inevitable entropy.

The Shape of Things to Come

This work, a carefully constructed spell against the unruly ghosts of nuclear forces, offers not so much a destination as a vantage point. The contour deformation, a clever trick to tame infinities, merely shifts the burden – the true wilderness lies in higher orders. The power counting, a fragile scaffolding built on assumptions, will inevitably meet a reality that refuses neat categorization. It’s a beautiful, temporary order imposed on inherent chaos.

The immediate future isn’t about achieving ‘accuracy,’ a phantom goal. It’s about systematically cataloging the failures of these perturbative expansions. Where do they break down, and how? The true prize won’t be matching experimental data-data is always right, until it hits production-but understanding the limitations of this particular method of persuasion. One suspects that truly robust predictions will require embracing the non-perturbative, a realm where the whispers become a roar.

Ultimately, this framework, like all frameworks, is a map drawn before fully exploring the territory. The next step isn’t to refine the map, but to venture into the fog, armed with the knowledge that every calculation is a temporary truce with uncertainty. The goal isn’t to solve the nucleus, but to domesticate the chaos, to learn its rhythms, and to anticipate its next move.

---

Original article: https://arxiv.org/pdf/2602.15453.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

• Mewgenics Tink Guide (All Upgrades and Rewards)
• Jujutsu Kaisen Modulo Chapter 23 Preview: Yuji And Maru End Cursed Spirits
• 8 One Piece Characters Who Deserved Better Endings
• Top 8 UFC 5 Perks Every Fighter Should Use
• How to Play REANIMAL Co-Op With Friend’s Pass (Local & Online Crossplay)
• One Piece Chapter 1174 Preview: Luffy And Loki Vs Imu
• How to Discover the Identity of the Royal Robber in The Sims 4
• How to Unlock the Mines in Cookie Run: Kingdom
• Sega Declares $200 Million Write-Off
• Full Mewgenics Soundtrack (Complete Songs List)

2026-02-18 20:25