Unlocking the Secrets of Baryons: A New Look at Diquark Mass

Author: Denis Avetisyan

A lattice QCD study provides crucial insights into the fundamental building blocks of matter by precisely determining the mass of scalar diquarks and characterizing their interactions.

The interplay between quarks and diquarks is governed by a potential energy landscape-a fundamental force shaping the architecture of matter itself-that dictates their binding and subsequent decay over time.

This research utilizes an extended HAL QCD method with a static quark to investigate the quark-diquark potential and address the challenges of color confinement in baryonic systems.

Understanding the internal dynamics of hadrons remains a fundamental challenge in quantum chromodynamics, particularly concerning the formation and properties of diquark correlations. This is addressed in ‘Diquark mass and quark-diquark potential by lattice QCD using an extended HAL QCD method with a static quark’, which presents a lattice QCD investigation determining a scalar diquark mass of approximately 1.241 GeV and characterizing the resulting quark-diquark potential as Cornell-type. Utilizing an extended HAL QCD method, this study circumvents the difficulties inherent in directly observing color-confined states. How might a more precise understanding of diquark masses and potentials refine our models of baryonic structure and strong interaction phenomena?

The Allure of the Unseen: Probing the Depths of Hadronic Matter

The fundamental constituents of matter – protons, neutrons, and the myriad particles discovered through high-energy physics – are not themselves elementary, but are instead complex systems governed by the strong force. This force, meticulously described by the theory of Quantum Chromodynamics (QCD), dictates interactions between quarks and gluons, binding them together to form hadrons. Unlike electromagnetism, which weakens with distance, the strong force increases with separation, confining quarks within these particles and preventing their observation in isolation. Therefore, a comprehensive understanding of QCD is not merely a theoretical pursuit, but a necessary condition for deciphering the very structure of matter, from the stability of atomic nuclei to the properties of exotic states like pentaquarks and tetraquarks – and ultimately, for a complete picture of the universe’s building blocks.

The formation of diquarks – hypothesized composite particles made of two quarks – presents a significant challenge to conventional calculations within the framework of Quantum Chromodynamics (QCD). Standard perturbative methods, which rely on approximating solutions based on small deviations from a simpler system, break down when applied to the strong interaction regime. This failure stems from the large coupling constant governing the strong force; unlike electromagnetism where interactions weaken with distance, the strong force remains strong even at relatively large separations within a diquark. Consequently, the infinite series used in perturbative calculations fail to converge, yielding meaningless results. Understanding diquark formation, therefore, demands sophisticated non-perturbative techniques capable of handling the full complexity of the strong interaction without relying on approximations that are invalid in this energy regime.

When exploring the potential existence of diquarks, conventional methods rooted in perturbation theory – techniques that rely on approximating solutions – prove inadequate due to the immense strength of the strong nuclear force. Consequently, physicists turn to non-perturbative approaches, most notably Lattice Quantum Chromodynamics (QCD). This computational technique discretizes spacetime into a four-dimensional lattice, allowing for the direct numerical solution of the equations governing the strong interaction. By simulating the behavior of quarks and gluons on this lattice, researchers can investigate the properties of diquarks – their masses, sizes, and potential roles in the structure of hadrons – in a regime where analytical calculations fail. These complex simulations offer a crucial pathway to understanding whether diquarks are merely theoretical constructs or genuine, observable particles contributing to the fundamental building blocks of matter, and offer insights into the non-perturbative nature of $QCD$ .

Calculations from wall-sourced two-point correlators reveal effective mass differences <span class="katex-eq" data-katex-display="false">\Delta m_{C\Gamma}</span> for baryonic states across different diquark channels. — Calculations from wall-sourced two-point correlators reveal effective mass differences $\Delta m_{C\Gamma}$ for baryonic states across different diquark channels.

Lattice QCD: A First-Principles Glimpse into Hadron Structure

Lattice Quantum Chromodynamics (Lattice QCD) offers a non-perturbative approach to studying the strong nuclear force, which governs interactions between quarks and gluons. This method addresses limitations of perturbative techniques applicable only at high energies. Lattice QCD discretizes spacetime into a four-dimensional lattice of points, replacing continuous space and time with a finite, manageable grid. This discretization allows for numerical solutions to the QCD equations of motion via Monte Carlo simulations. By performing calculations on this discrete spacetime, properties of hadrons-composite particles made of quarks and gluons-can be predicted directly from the fundamental parameters of QCD, such as quark masses and the strong coupling constant, without relying on phenomenological models. The accuracy of these predictions depends on the lattice spacing, with smaller spacing leading to more accurate results and requiring greater computational resources.

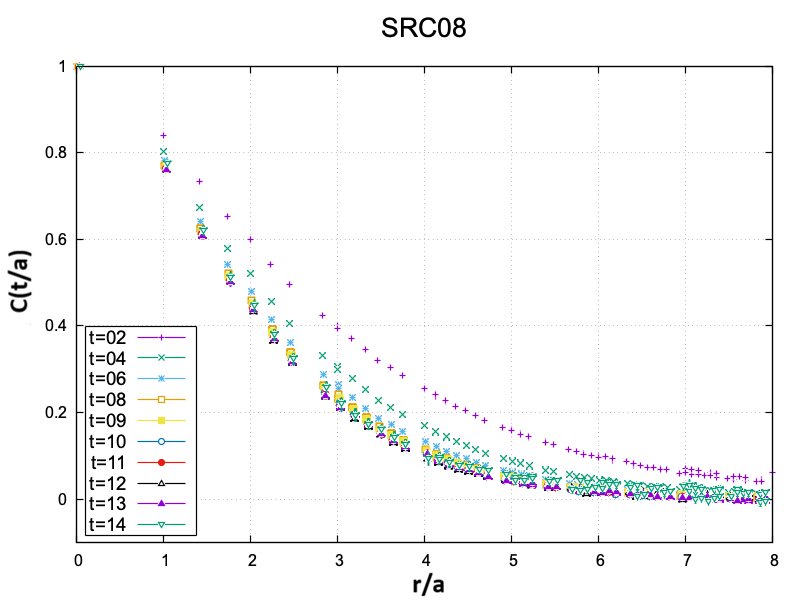
The investigation of diquark states within Lattice QCD relies heavily on the construction and analysis of correlation functions. Specifically, the Two-Point Correlator, denoted as $C_2(t) = \sum_x \langle 0 | O(x,t) O^\dagger(0,0) | 0 \rangle$ , is central to this process. This function quantifies the probability amplitude for a particle to propagate from an initial state at time $t=0$ to a final state at time $t$ . By analyzing the exponential decay of $C_2(t)$ , researchers can extract crucial information about the diquark’s mass and other relevant properties. The construction of appropriate operators $O(x,t)$ within the correlator, which couple to the desired diquark state, is critical for obtaining reliable results and necessitates a thorough understanding of the underlying quark-model assumptions and symmetries.

The accurate determination of diquark masses and properties from correlation function analysis within Lattice QCD necessitates a robust theoretical framework and careful control of discretization effects. Achieving this requires simulations performed at a sufficiently fine lattice spacing; analyses utilizing ensembles with a lattice spacing of approximately 0.1209 fm have proven effective in minimizing these effects. This spacing allows for a more accurate representation of the continuous spacetime limit, improving the precision with which diquark states – bound states of two valence quarks – can be characterized and their associated parameters, such as mass and decay constants, extracted. Systematic uncertainties arising from the discrete nature of spacetime are thus reduced, enabling reliable comparisons with experimental data and other theoretical calculations.

Convergence of four-point correlators demonstrates that exponentially smeared sources with shorter smearing lengths (<span class="katex-eq" data-katex-display="false">\exp(-r)</span>) converge faster than those with longer lengths (<span class="katex-eq" data-katex-display="false">\exp(-r/3)</span>) or a wall source. — Convergence of four-point correlators demonstrates that exponentially smeared sources with shorter smearing lengths ( $\exp(-r)$ ) converge faster than those with longer lengths ( $\exp(-r/3)$ ) or a wall source.

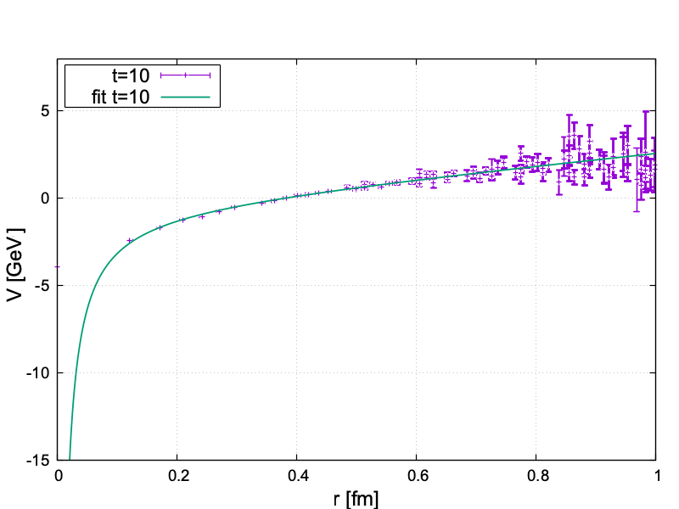
Modeling the Interaction: The Cornell Potential and HAL QCD

The interaction between quarks and diquarks is frequently modeled using the Cornell potential, a non-relativistic potential that effectively describes the strong force. This potential consists of two primary terms: a Coulombic term, $- \frac{\alpha}{r}$ , representing the short-range interaction, and a linear confining term, $\sigma r$ , which dominates at larger separations. The Coulombic component arises from the exchange of gluons, while the linear term models the color flux tube formation responsible for quark confinement. The strength of the Coulombic interaction is defined by the fine-structure constant α, and the string tension is represented by σ. This combination provides a reasonable approximation of the quark-quark and quark-diquark interactions within hadrons, allowing for calculations of their properties and decay modes.

The HAL QCD method addresses the difficulties inherent in defining a bound state pole within quark-diquark models by employing a momentum-space formulation and focusing on calculating observable quantities rather than directly solving for bound state energies. This is achieved through the calculation of the four-point Green’s function, or four-point correlator, which allows for the extraction of the Nambu-Bethe-Salpeter (NBS) wavefunction Ψ and the corresponding prepotential $V$ . By analyzing these quantities, the method circumvents the need for explicitly locating a pole in the scattering matrix, providing a systematic and well-defined pathway to construct and analyze quark-diquark interactions without relying on potentially ambiguous pole definitions. Calculations within this framework, performed with a pion mass of 1014 MeV and a nucleon mass of 2026 MeV, demonstrate the viability of this approach for studying hadron structure.

The HAL QCD method determines quark-diquark interactions by calculating the four-point correlation function $\Gamma_4$ , which provides information about the scattering amplitude. From $\Gamma_4$ , the Nambu-Bethe-Salpeter (NBS) wavefunction, Ψ, is extracted, describing the bound state. The potential governing the interaction is then determined via the prepotential, derived from the NBS wavefunction. These calculations, performed with a pion mass of 1014 MeV and a nucleon mass of 2026 MeV, allow for the systematic determination of the quark-diquark potential without direct reference to a pole position, circumventing a key challenge in defining bound states within quantum field theory.

Addressing Ambiguities: The Extended HAL QCD Method

Conventional HAL QCD calculations, while effective for baryon spectroscopy, encounter ambiguities stemming from the selection of input parameters. Specifically, the precise value assigned to the charm quark mass $m_c$ significantly impacts results; variations within the theoretically allowed range can lead to discrepancies in calculated energy levels and hadron properties. This sensitivity arises because the HAL QCD method relies on constructing effective potentials from scattering amplitudes, and the parameters used to regularize these calculations, including $m_c$ , introduce model dependence. Consequently, the robustness of predictions is limited by the uncertainty in these input parameters, necessitating careful consideration and potentially leading to systematic errors in extracted physical quantities.

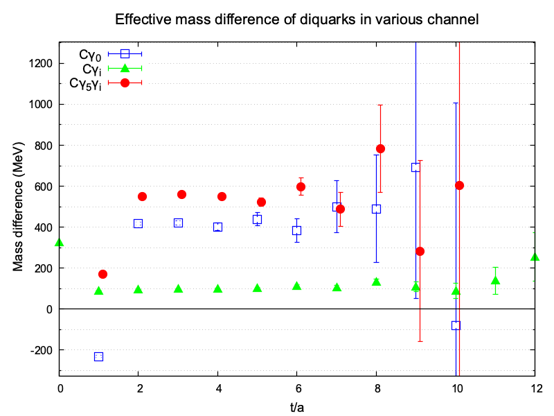
The Extended HAL QCD method addresses parameter ambiguities inherent in conventional HAL QCD calculations by incorporating a static quark. This approach utilizes the properties of a static quark – infinite mass and a fixed position – to provide a well-defined reference point within the HAL QCD framework. By including this static quark, calculations become less sensitive to the arbitrary choices of parameters like the charm quark mass, which typically introduce uncertainties in determining hadron properties. The inclusion of a static quark effectively stabilizes the calculations and allows for a more robust and reliable determination of quantities such as diquark masses and interactions, ultimately improving the predictive power of the HAL QCD method.

The Extended HAL QCD method facilitates a more precise determination of scalar diquark mass, yielding a value of approximately 1.241 GeV. This result is notable as it represents roughly two-thirds of the nucleon mass, which is approximately 1.35 GeV. The correlation between diquark mass and nucleon mass suggests a significant contribution of diquark correlations to the overall structure and mass of nucleons, providing quantitative data for theoretical models aiming to describe baryon structure. This established mass value serves as a benchmark for validating and refining future calculations and theoretical predictions regarding diquark and nucleon properties.

Implications for Dense Matter: Color Superconductivity

The emergence of scalar diquarks-composite particles formed by two quarks-significantly alters the equation of state for matter at extraordinarily high densities, such as those found within neutron stars. These diquarks aren’t simply bound states; their unique properties allow them to condense into a fundamentally new state of matter. This condensation effectively reduces the number of independent degrees of freedom, lowering the energy per baryon and influencing the star’s mass-radius relationship. The presence of these scalar diquarks suggests a softening of the equation of state, potentially impacting the maximum mass a neutron star can achieve before collapsing into a black hole, and opening possibilities for the existence of stable, hyperdense stellar objects beyond current theoretical limits. The influence extends to the star’s cooling rate and internal structure, making scalar diquark condensation a crucial factor in understanding the behavior of matter under the most extreme conditions in the universe.

The condensation of scalar diquarks into a Color Superconductivity phase represents a dramatic shift in the behavior of matter at extraordinarily high densities, such as those found within neutron stars. This phase isn’t simply a change of state; it fundamentally alters the strong force interactions between quarks, effectively reducing the usual confinement and allowing them to move with remarkably little resistance. Consequently, neutron stars exhibiting this color superconductivity are predicted to possess altered cooling rates, modified mass-radius relationships, and potentially even different gravitational wave signatures during mergers. The implications extend to the behavior of quark matter in hypothetical ‘strange stars’ and offer a novel perspective on the equation of state governing ultra-dense astrophysical objects, potentially resolving long-standing puzzles regarding their internal structure and evolution.

Recent calculations of string tension within dense matter reveal a value of 510 MeV, a notable increase from the conventionally accepted figure of approximately 440 MeV. This seemingly subtle difference has significant ramifications for the behavior of matter at extreme densities, particularly within neutron stars. String tension dictates the energy cost associated with breaking a flux tube – a confined magnetic field line – and a higher value implies stronger interactions between constituent quarks. Consequently, this enhanced interaction strength influences the equation of state of dense matter, potentially altering the mass-radius relationship of neutron stars and affecting the dynamics of color superconductivity – a state where quarks pair up due to strong interactions, leading to zero electrical resistance. These findings suggest that the internal structure and observational properties of dense astrophysical objects may deviate from predictions based on the lower, conventional string tension, offering a new avenue for probing the fundamental physics of matter under extreme conditions.

The pursuit to define the quark-diquark potential, as detailed in this study, mirrors the inevitable entropy of any complex system. The HAL QCD method, extended to grapple with color confinement, isn’t merely a technical solution but a testament to adaptation in the face of decay. As Friedrich Nietzsche observed, “That which does not kill us makes us stronger.” This rings true; each methodological hurdle overcome, each refinement to address the limitations of confinement, strengthens the understanding of these baryonic systems. The determined mass of the diquark – 1.241 GeV – isn’t a final answer, but a marker along the timeline, a point of truth established amidst the inherent instability of quantum chromodynamics.

What Lies Ahead?

The determination of a diquark mass, as presented, is not an arrival, but a calibration. It establishes a point on the decay curve of color confinement, acknowledging that even stable baryons are, in time, susceptible to the entropic pull toward constituent quarks. The calculated potential, while illuminating the interaction, merely maps the contours of a fundamentally unstable system. Technical debt accumulates, even in the most rigorous calculations-approximations, however elegant, introduce fissures that widen with subsequent refinements.

Future iterations must confront the limitations inherent in static quark approximations. A truly dynamic picture-one accounting for the internal motion and relativistic effects-will necessitate significantly increased computational resources. The challenge isn’t simply to achieve greater precision, but to understand whether the observed diquark is a fleeting resonance, a transient phase of temporal harmony, or a genuinely stable entity within the broader landscape of hadronic matter.

Ultimately, this work highlights a crucial point: the search for stable color-singlet combinations is less about discovering fundamental building blocks, and more about charting the inevitable fragmentation of complex systems. Uptime, in any system-computational or physical-is a rare and temporary reprieve from the universal tendency toward disorder. The next step requires embracing this decay, not resisting it, and mapping the pathways through which confinement eventually yields to the freedom of constituent quarks.

Original article: https://arxiv.org/pdf/2601.10091.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/