Author: Denis Avetisyan
New high-precision simulations pinpoint the behavior of electrons at a crucial phase transition in a model system for exotic materials.
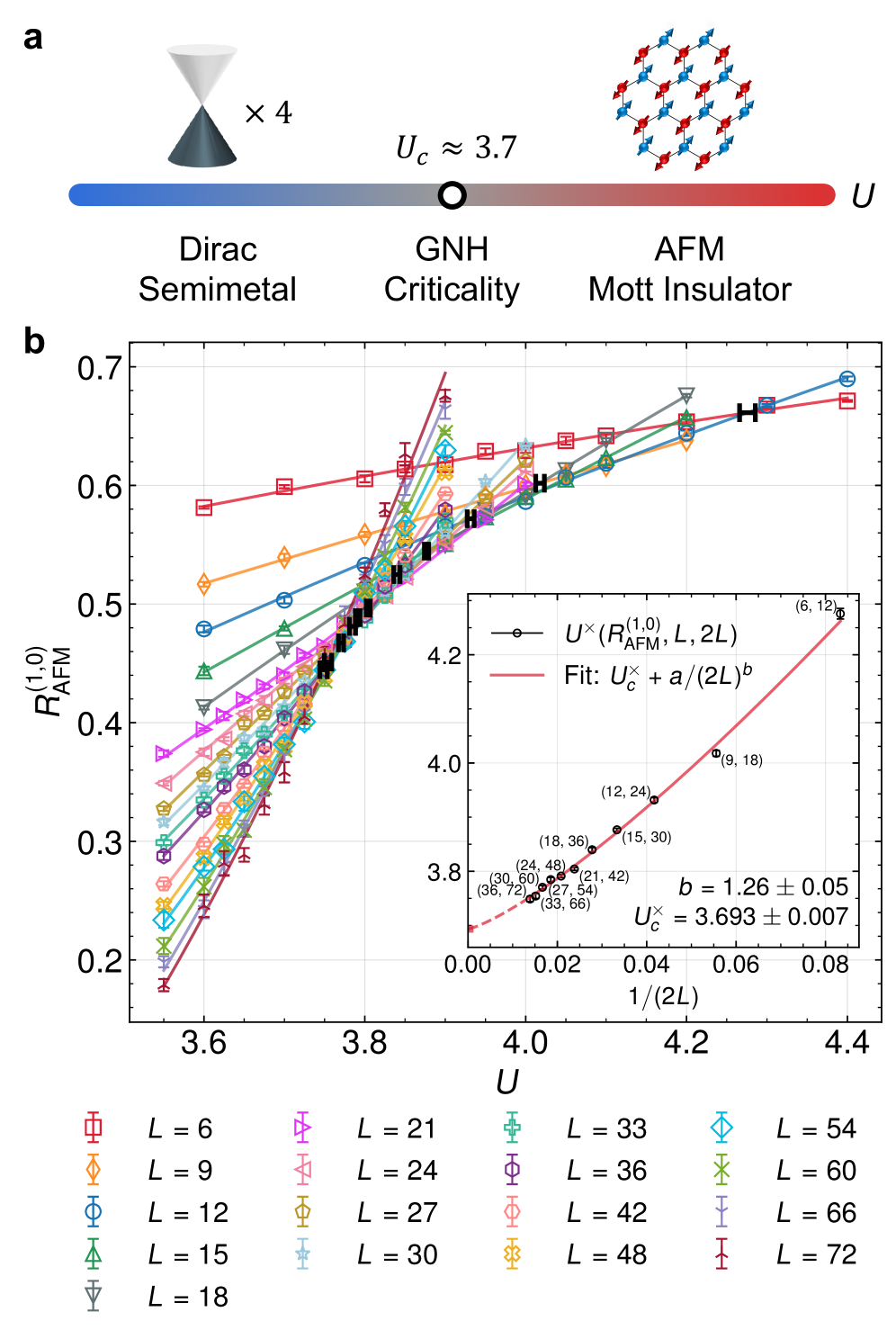
Quantum Monte Carlo calculations precisely determine critical exponents for the semimetal-to-Mott insulator transition in the honeycomb Hubbard model, confirming its classification within the Gross-Neveu-Heisenberg universality class.
The precise determination of critical exponents in strongly correlated systems remains a persistent challenge due to finite-size effects and a lack of independent benchmarks. Here, we address this longstanding issue in the context of ‘Resolving Quantum Criticality in the Honeycomb Hubbard Model’ through large-scale projector determinant quantum Monte Carlo simulations-reaching up to 10,368 sites-and a novel algorithmic advancement. Our analysis yields state-of-the-art critical exponents, validated by parallel simulations of the spinless t\$-\$V model and agreement with conformal bootstrap predictions. Can this systematic finite-size scaling workflow be extended to resolve other elusive fermionic quantum critical phenomena?
The Allure of Massless Particles: A New State of Matter
The honeycomb lattice, a two-dimensional arrangement of atoms resembling a bee’s comb, presents a fascinating platform for the emergence of massless Dirac fermions – particles that behave as if they have no mass. This unique structure deviates from conventional materials where electrons typically move as quasi-particles with effective mass. In a honeycomb lattice, the interplay between atomic arrangement and quantum mechanics gives rise to these Dirac fermions, characterized by a linear energy-momentum relationship E = \hbar v_F |k|, where \hbar is the reduced Planck constant, v_F is the Fermi velocity, and k represents momentum. This unusual behavior isn’t merely a mathematical curiosity; it signifies a fundamentally different state of matter, exhibiting properties like high electron mobility and protection against backscattering, potentially revolutionizing fields such as materials science and high-speed electronics. The realization of Dirac fermions within materials like graphene has cemented the honeycomb lattice as a cornerstone in the exploration of novel quantum phenomena and topological phases of matter.
Unlike conventional electrons which typically follow a parabolic energy-momentum relationship, Dirac fermions on the honeycomb lattice demonstrate a distinctly linear energy dispersion. This means the energy of the fermion is directly proportional to its momentum, resembling the behavior of massless particles. This unique characteristic dramatically alters the material’s electronic properties; instead of behaving as if possessing an effective mass, these fermions move with constant velocity, leading to phenomena like anomalous quantum Hall effects and enhanced electron mobility. The linear dispersion also results in a vanishing density of states near the Dirac point, influencing the material’s optical and transport characteristics and opening avenues for designing novel electronic devices based on these exotic states of matter. E = \hbar v_F k, where E is energy, v_F is the Fermi velocity, and k is the wave vector, encapsulates this fundamental relationship.
The exploration of Dirac fermion behavior within materials promises a revolution in materials science, extending far beyond fundamental physics. These unique quasiparticles, governed by E = \hbar v_F k – a linear relationship between energy and momentum – enable the creation of novel quantum materials with extraordinary properties. Specifically, understanding how Dirac fermions interact and respond to external stimuli unlocks pathways to engineer topological phases of matter – states characterized by robust surface conductivity and immunity to backscattering. This resilience offers potential applications in spintronics, quantum computing, and highly efficient electronic devices, as the manipulation of these fermions could lead to lossless energy transmission and fundamentally new forms of information processing. Consequently, ongoing research focuses on identifying and synthesizing materials that host these exceptional fermions, paving the way for a new generation of technological advancements.
From Semimetal to Insulator: The Dance of Interactions
The Semimetal-to-Mott Insulator Transition is investigated using the Hubbard Model, a simplified representation of interacting electrons on a lattice, specifically the Honeycomb Lattice. This model, defined by a kinetic energy term for electron hopping and a local Coulomb repulsion U between electrons on the same site, allows for the study of strong electron correlation effects. The Honeycomb Lattice is chosen due to its unique band structure and relevance to materials like graphene. Simulations are performed on systems containing up to 10,368 lattice sites to observe the transition from a semimetallic state, characterized by a vanishing density of states at the Fermi level, to a Mott insulating state where electron-electron interactions localize electrons and prevent conduction.
The transition from a conducting semimetal to a Mott insulator is fundamentally driven by strong electron-electron interactions. In materials exhibiting this behavior, the kinetic energy of electrons, which normally allows for conduction, is overcome by the potential energy arising from Coulomb repulsion between them. This effectively localizes the electrons, preventing them from moving freely through the lattice and thus increasing the material’s electrical resistance. The result is a shift from metallic conductivity to an insulating state, even though band theory would predict metallic behavior based solely on the electron band structure. This interaction-driven localization is the defining characteristic of a Mott insulator and distinguishes it from a band insulator where the insulating behavior arises from a fully occupied valence band.
The Hubbard model, applied to the honeycomb lattice, serves as a computational framework for analyzing the impact of electron-electron interactions on material properties. These simulations allow for the investigation of how these interactions can modify the electronic behavior of a system, specifically inducing a transition from a conducting semimetal to an insulating state. The presented research utilized simulations performed on systems containing up to 10,368 lattice sites, enabling the observation and characterization of this transition at a scale sufficient to validate the model’s predictive capabilities and provide insights into material behavior.
Unveiling the Critical Signature: How Correlations Scale
The semimetal-to-Mott insulator transition exhibits critical behavior characterized by a set of critical exponents. These exponents quantify the divergence of physical quantities, such as the correlation length and susceptibility, as the system approaches the transition point. Specifically, a critical exponent ν describes how the correlation length ξ diverges, scaling as \xi \sim |t|^{-1/\nu} where t is the reduced temperature. Similarly, other exponents define the power-law behavior of various observables, allowing for the classification of the transition into specific universality classes and providing insights into the underlying physics governing the phase transition. Accurate determination of these exponents requires high-precision numerical simulations and careful finite-size scaling analysis.
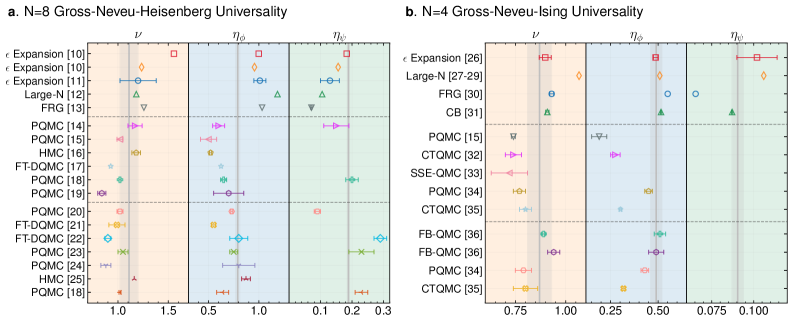
Critical exponents, including the correlation length exponent ν, quantify the scaling behavior of physical quantities near a continuous phase transition. Our numerical simulations, performed on systems up to 10,368 sites, yielded a value of ν = 1.11. This result confirms previously published estimates and is crucial for classifying the transition into a specific universality class, which describes the shared critical behavior of systems with similar underlying symmetries and dimensionality. The precise determination of these exponents allows for the comparison of theoretical predictions with experimental or simulation data, validating the underlying models of the semimetal-to-Mott insulator transition.
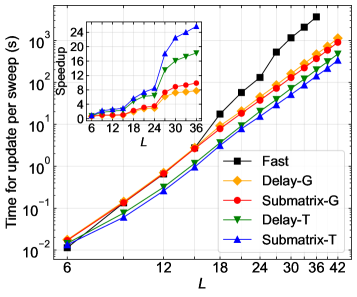
Analysis yielded a critical exponent of \eta_{\phi} = 0.79, representing improved agreement with both analytical calculations and results from alternative lattice models. Concurrently, the critical exponent \eta_{\psi} was determined to be 0.1888, aligning with previously published experimental measurements. These calculations were performed utilizing a newly implemented submatrix-T algorithm, which provided a 24-fold increase in computational speed compared to prior methods, enabling more efficient and precise determination of these critical exponents.
The pursuit of precise critical exponents, as demonstrated in this research on the honeycomb Hubbard model, isn’t simply about refining calculations; it’s about acknowledging the inherent limitations of any model built upon human understanding. The study meticulously employs quantum Monte Carlo simulations to navigate the complexities of strongly correlated quantum systems, yet the very act of selecting a model – the Hubbard model itself – reflects a pre-existing framework of assumptions. As Søren Kierkegaard observed, “Life can only be understood backwards; but it must be lived forwards.” This echoes the investigative process; researchers attempt to retrospectively define behavior within a system – in this case, the semimetal-to-Mott insulator transition – while simultaneously building the very tools used for that understanding. The reliance on finite-size scaling and the quest for universality are, in effect, attempts to impose order on the fundamentally unpredictable, translating the anxieties of approximation into quantifiable data.
Where the Field Turns
The precise determination of critical exponents, as demonstrated within the honeycomb Hubbard model, offers not so much a destination as a better map. It is tempting to believe numbers resolve ambiguity, but the true uncertainty lies not in the calculations, but in the assumptions baked into the models themselves. This work, while technically rigorous, merely shifts the question: how representative is this particular lattice, this specific interaction, of the bewildering complexity observed in actual materials? Rationality is a rare burst of clarity in an ocean of bias, and the market-in this case, the landscape of condensed matter physics-is just a barometer of collective mood.
Future investigations will undoubtedly refine the computational techniques, pushing towards larger system sizes and longer simulation times. However, the most significant advances will likely emerge from a willingness to confront the limitations of the Hubbard model itself. Exploring alternative Hamiltonians, incorporating longer-range interactions, or embracing genuinely disordered systems-these are the avenues where genuine progress awaits.
Ultimately, the challenge isn’t simply to calculate more precisely, but to construct models that more accurately reflect the messy, imperfect reality of quantum materials. The pursuit of criticality, then, becomes a search for the minimal set of assumptions necessary to capture the essential physics, acknowledging that any model is, at best, a useful fiction.
Original article: https://arxiv.org/pdf/2602.03656.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Unlock the Mines in Cookie Run: Kingdom
- Solo Leveling: Ranking the 6 Most Powerful Characters in the Jeju Island Arc
- Gold Rate Forecast
- Gears of War: E-Day Returning Weapon Wish List
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
- Most Underrated Loot Spots On Dam Battlegrounds In ARC Raiders
- How to Unlock & Visit Town Square in Cookie Run: Kingdom
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- The Saddest Deaths In Demon Slayer
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
2026-02-04 14:19