Author: Denis Avetisyan
Researchers have achieved a comprehensive solution for describing string behavior in a complex, three-dimensional space, bridging the gap between theoretical physics and concrete calculations.
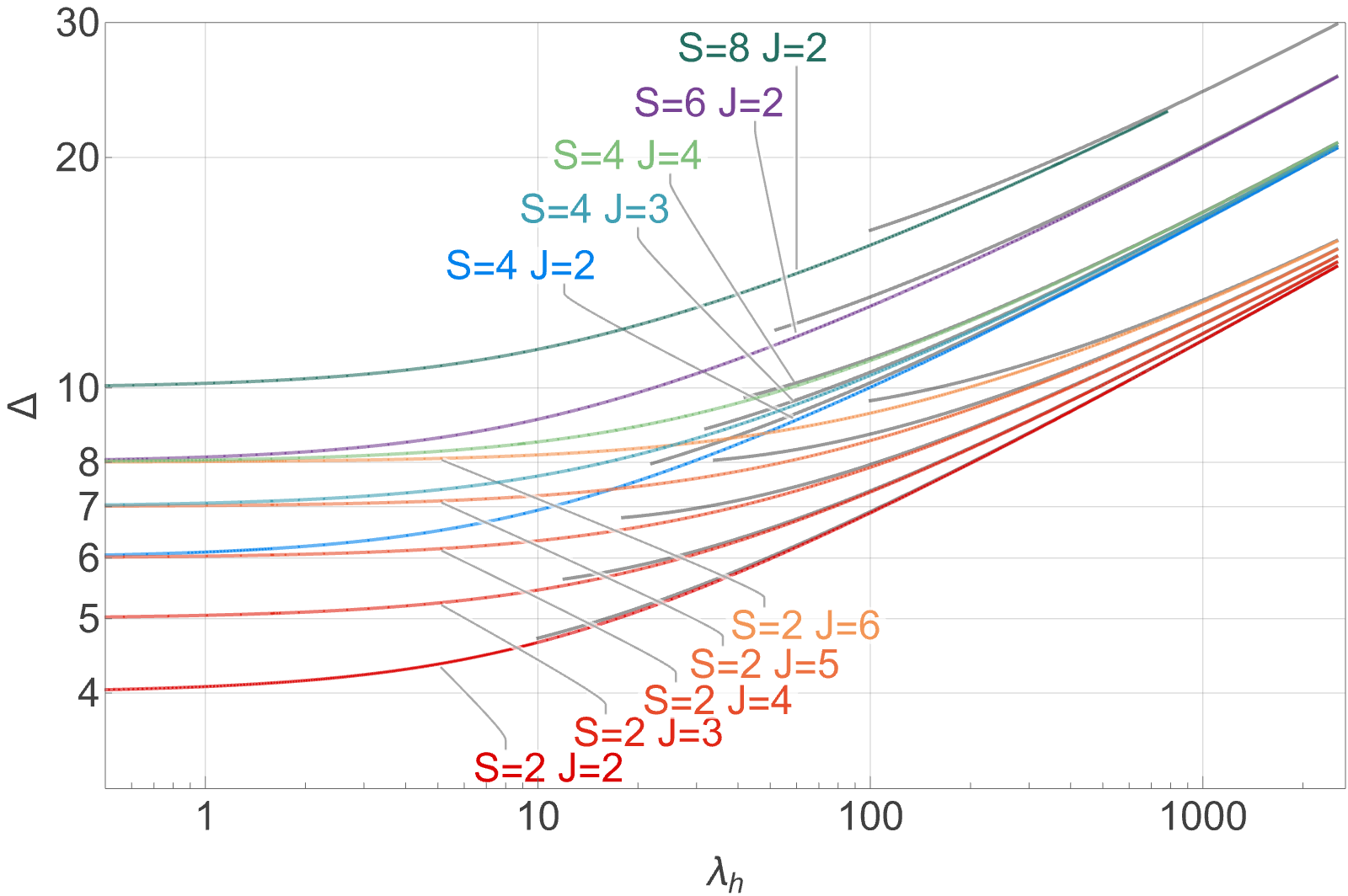
This work presents the first complete solution of the AdS3 Quantum Spectral Curve across a wide range of coupling strengths, providing a full spectrum of string states and advancing the AdS/CFT correspondence.
Despite longstanding expectations from the AdS/CFT correspondence, a complete analytic understanding of string dynamics in Anti-de Sitter space has remained elusive. This is addressed in ‘Short Strings in Three-Dimensional Anti-de Sitter Space: from Weak to Strong Coupling’, where the authors present the first numerical solution of the Quantum Spectral Curve for strings on AdS_3 \times S^3 \times T^4 across the entire coupling range. The resulting spectrum reveals universal scaling behaviour at strong coupling, connecting to flat-space string theory, and demonstrates integrable spin-chain physics at weak coupling, with precise subleading corrections. Will this approach unlock a broader understanding of quantum gravity and holographic duality in more complex spacetimes?
The Fragile Symmetry of Weak Interactions
Perturbative string theory, the dominant approach to exploring this complex framework, fundamentally depends on a mathematical condition known as ‘weak coupling’. This regime arises when interactions between strings are relatively feeble, allowing physicists to treat these interactions as small corrections to a simpler, solvable system. By employing a technique analogous to approximations used in other areas of physics, such as quantum electrodynamics, calculations become tractable – meaning they can be performed with existing mathematical tools. Essentially, the theory is expanded around a point of minimal interaction, yielding increasingly accurate results as more correction terms are included. While this approach has provided profound insights into the nature of strings and the potential unification of forces, it’s important to note that the weak coupling regime represents only one facet of string theory’s full, potentially far more intricate, behavior.
The foundation of perturbative string theory rests on the ability to simplify immensely complex calculations through approximation within the ‘weak coupling’ regime. This approach mirrors techniques used in other areas of physics, where a system’s behavior is understood by starting with a readily solvable point – a simplified baseline – and then incrementally adding complexities as small corrections. These corrections, representing deviations from the baseline, are calculated order by order, building up a progressively more accurate picture of the system’s true dynamics. Essentially, the weak coupling regime allows physicists to treat string interactions as minor perturbations to a free string, vastly reducing the computational burden and making theoretical progress possible; the more weakly the strings interact, the more accurate this approximation becomes, allowing for predictions about the universe at its most fundamental level.
While perturbative string theory provides valuable insights within the realm of weak interactions – where calculations remain manageable – a complete understanding of string dynamics necessitates venturing beyond this simplified regime. Recent theoretical advancements demonstrate that exploring strong coupling – characterized by intense interactions – demands novel analytical tools and approaches. These calculations, often leveraging concepts from duality and holography, reveal connections between seemingly disparate physical systems and offer glimpses into the non-perturbative nature of strings. Such investigations aren’t merely extending existing techniques; they’re forging entirely new mathematical frameworks to tackle the complexities arising when strings are subject to extreme forces, ultimately aiming to unlock a more complete picture of the universe at its most fundamental level.
Operator Dimensions and the Echoes of Conformal Symmetry
The Virasoro-Shapiro amplitude is a computational technique used to determine deviations from the expected scaling dimensions of operators in a conformal field theory. This method relies on analyzing the exchange of energy and momentum between operators, effectively calculating corrections to the operator’s dimension based on the system’s dynamics. The amplitude provides a systematic way to quantify these corrections, enabling precise calculations of how operator dimensions are modified due to interactions and external influences, and is particularly useful in contexts where exact solutions are unavailable, offering an approximation scheme based on conformal symmetry principles.
The Virasoro-Shapiro amplitude exploits the principles of conformal symmetry to quantify deviations from the expected scaling dimensions of operators. Conformal symmetry dictates how fields transform under coordinate changes, and its preservation, even when slightly broken, allows for precise calculations of dimension corrections. These calculations reveal that operators do not adhere strictly to free-field scaling, exhibiting shifts in their dimensions due to interactions. Critically, the amplitude’s results align with predictions derived from classical string theory, specifically regarding the expected magnitude and form of these corrections, thereby providing a consistency check and a pathway for relating field theory to string theory.
The Virasoro-Shapiro amplitude utilizes Superconformal Primary states as fundamental inputs for determining corrections to operator dimensions. These states, possessing specific transformation properties under conformal transformations, allow for the computation of deviations from expected scaling behavior. Calculations based on these states yield a leading order coefficient of 2\sqrt{S} for the dimension correction, where S represents the central charge. This result is significant as it directly corresponds to predictions derived from classical string theory, validating the method’s efficacy in probing corrections to operator dimensions within a conformal field theory framework.
Discretization and Integrability: Approximating String Dynamics
The Spin Chain model provides an approximation of string dynamics in Anti-de Sitter (AdS3) backgrounds by representing the string worldsheet as a one-dimensional chain of spins. This discretization allows for the transformation of the complex, continuous problem of string theory into a more tractable, combinatorial framework. Specifically, states of the string are mapped to eigenstates of the spin chain Hamiltonian, enabling calculations of string scattering amplitudes and correlation functions. The model leverages integrability – a property of certain quantum systems – to facilitate exact solutions and provide insights into the behavior of strings in these spacetimes. The effectiveness of this approximation relies on identifying appropriate mappings between string theory parameters and the parameters defining the spin chain, such as the chain length and the strength of interactions between spins.
The spin chain approximation addresses the complexities of string dynamics by representing the string’s two-dimensional worldsheet as a one-dimensional chain of discrete sites, each possessing an associated spin. This discretization replaces the need to solve continuous partial differential equations – typically arising in classical string theory – with a combinatorial problem involving a finite number of degrees of freedom. Each point on the discretized worldsheet is then treated as a spin, and interactions between neighboring spins define the system’s Hamiltonian. Consequently, calculations shift from solving functional equations to evaluating matrix elements and performing algebraic manipulations on the resulting spin chain operators, significantly simplifying the analysis of string behavior.
The spin chain approximation to string dynamics in AdS3 backgrounds is fundamentally valid within the weak coupling regime; however, recent advancements utilizing the Quantum Spectral Curve (QSC) have expanded its applicability to strong coupling scenarios. QSC calculations have revealed a λh^{-1/2} correction to the energy spectrum, where λ represents the ‘t Hooft coupling and h is the conformal dimension. Critically, these calculations demonstrate a numerical uncertainty in determining the scaling dimension Δ of only 10-10, representing a significant improvement in precision and validating the method’s efficacy even outside the traditional weak coupling limit.
The pursuit of a complete spectrum, as demonstrated in this exploration of AdS3 Quantum Spectral Curve solutions, echoes a fundamental truth about complex systems. Just as structures inevitably evolve and adapt, the successful navigation across varying coupling ranges-from weak to strong-reveals a system’s inherent capacity for resilience. This mirrors the idea that incidents aren’t failures, but steps toward maturity. As Jean-Jacques Rousseau observed, “The more we sweat in peace, the less we bleed in war.” Similarly, the rigorous mathematical work presented here-the ‘sweat’ of theoretical physics-strengthens the framework for understanding string theory and the holographic principle, allowing it to withstand the challenges of increasingly complex conditions.
What Lies Ahead?
The resolution of the AdS3 Quantum Spectral Curve across a broader coupling range is not an arrival, but a refinement of the map. This work demonstrates a coherence between seemingly disparate descriptions – integrable spin chains and string theory in AdS3 – yet it does not eliminate the fundamental questions. The achieved spectrum, while comprehensive, exists within a specific framework. The universe, of course, rarely conforms to convenient frameworks.
Integrability, though a powerful tool, is a special case. Most systems are not so neatly ordered. The persistence of this approach invites inquiry into the fate of spectra as integrability breaks down, as the elegant curves fray into noise. One might consider this not a failure, but an honest depiction of decay – stability, after all, is often merely a delayed disintegration.
Future investigations will likely turn toward the inclusion of R-R charges, and the exploration of non-integrable deformations. These are not merely technical extensions; they represent a confrontation with the inevitable. Systems age not because of errors in the calculation, but because time is inevitable. The true challenge lies not in perfecting the description of a stable state, but in understanding the graceful – or ungraceful – manner of its passing.
Original article: https://arxiv.org/pdf/2601.21992.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Gold Rate Forecast
- How to Unlock the Mines in Cookie Run: Kingdom
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
- How To Upgrade Control Nexus & Unlock Growth Chamber In Arknights Endfield
- Jujutsu: Zero Codes (December 2025)
- Most Underrated Loot Spots On Dam Battlegrounds In ARC Raiders
- Top 8 UFC 5 Perks Every Fighter Should Use
- Gears of War: E-Day Returning Weapon Wish List
- All Pistols in Battlefield 6
- Byler Confirmed? Mike and Will’s Relationship in Stranger Things Season 5
2026-01-31 14:19