Author: Denis Avetisyan
A novel geometric approach simplifies the classification of multi-qubit entanglement, offering a faster alternative to traditional decomposition methods.
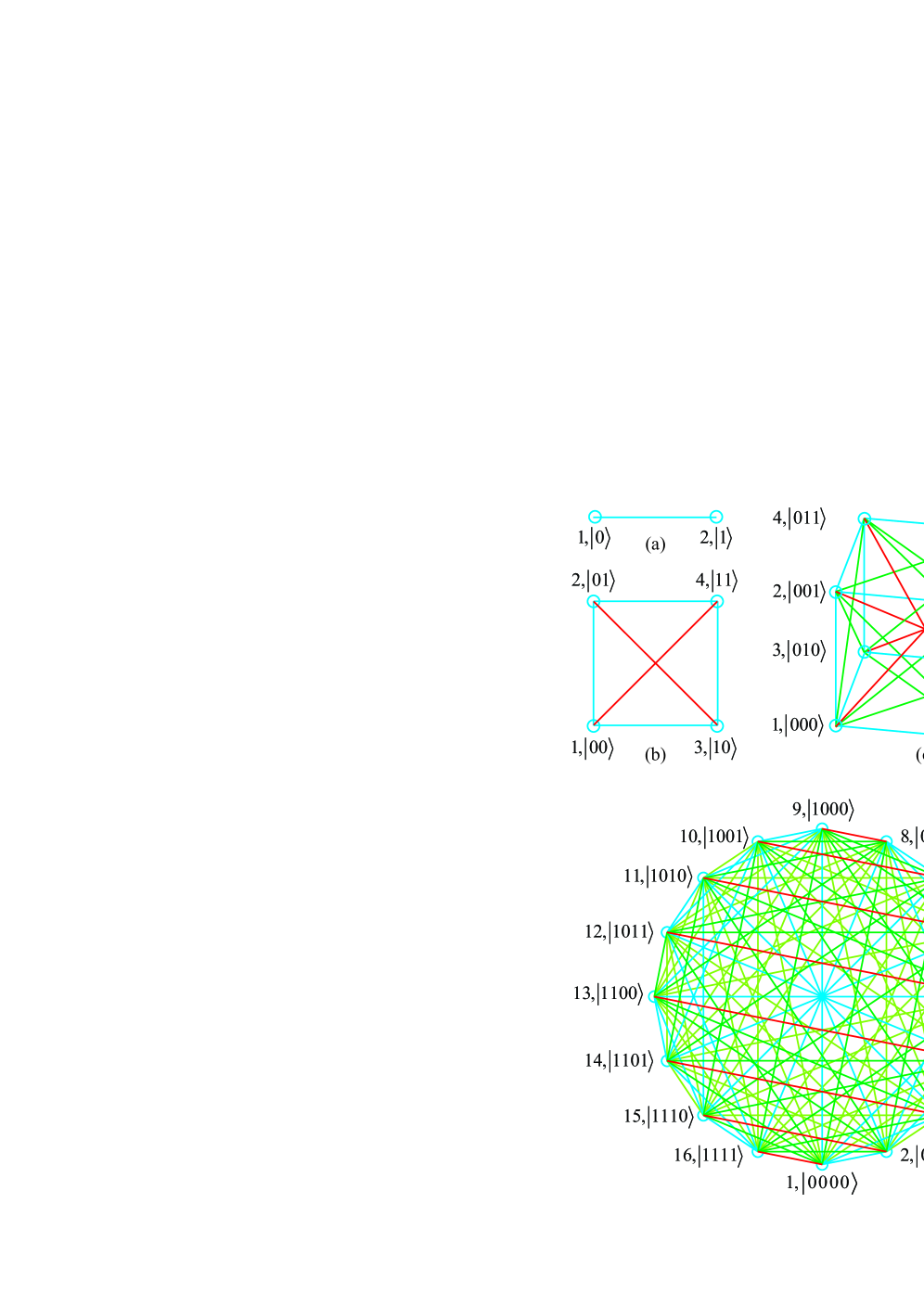
This review introduces a ‘support taxonomy’ based on Boolean cube geometry to efficiently analyze the separability conditions of qubit registers.
Determining the separability of multi-qubit states remains a computationally intensive challenge in quantum information science. This is addressed in ‘On the quantum separability of qubit registers’, which introduces a framework leveraging Boolean cube geometry to classify qubit states based on the combinatorial structure of their computational basis support. The authors demonstrate that this ‘support taxonomy’ allows for efficient identification of both separable states and those fundamentally exhibiting multipartite entanglement, offering a scalable alternative to methods like Schmidt decomposition. Could this geometric approach unlock new strategies for entanglement diagnostics, circuit design, and even quantum error correction?
The Paradox of Entanglement: A Fragile Connection
Quantum entanglement demonstrates a profoundly counterintuitive connection between particles, regardless of the distance separating them. This phenomenon posits that two or more particles become linked in such a way that they share the same fate, meaning a measurement performed on one instantly influences the state of the other – a correlation that defies classical physics’ insistence on locality and independence. Traditionally, objects are considered distinct and influenced only by their immediate surroundings; entanglement, however, suggests a deeper, non-local reality where particles can be intrinsically linked, exhibiting coordinated behavior even when spatially separated by vast distances. This challenges the long-held assumption that an object’s properties are determined solely by its own internal state and immediate environment, hinting at a fundamental interconnectedness woven into the fabric of the quantum world and prompting revisions to our understanding of how information and correlations operate at the most basic level of reality.
The remarkable connection forged through quantum entanglement, while seemingly instantaneous, proves surprisingly vulnerable to environmental interactions. This fragility manifests as decoherence – the loss of quantum information due to the system’s coupling with its surroundings. Essentially, any unintended measurement or disturbance collapses the entangled state, destroying the correlation between particles and hindering its use for transmitting or processing information. This creates a fundamental paradox: entanglement offers a potentially revolutionary pathway for quantum technologies, yet maintaining this connection long enough to perform useful computations or secure communications remains a significant hurdle. The fleeting nature of entanglement demands increasingly sophisticated methods of isolation and error correction to shield these delicate quantum states from the disruptive influence of the outside world, representing a key focus of current research.
The promise of quantum technologies – from secure communication to exponentially faster computation – hinges on the ability to reliably create and maintain entanglement, a notoriously delicate quantum state. While entanglement demonstrably links particles regardless of distance, its susceptibility to decoherence – the loss of quantum information due to environmental interactions – presents a significant hurdle. Researchers are actively investigating the precise limits of entanglement longevity and fidelity under various conditions, striving to develop error correction protocols and robust qubit designs. Determining these boundaries isn’t merely an academic exercise; it directly informs the scalability of quantum devices and the feasibility of practical applications. Without a comprehensive understanding of what degrades entanglement and how to mitigate these effects, the full potential of quantum technologies will remain unrealized, necessitating continued innovation in materials science, control systems, and quantum error correction techniques.
Mapping Entanglement: The Geometry of State Structure
The n-cube Support provides a geometrical framework for analyzing quantum state entanglement by representing a quantum state’s wavefunction as a point within an n-dimensional hypercube, where each dimension corresponds to a degree of freedom of the |ψ⟩ state. The Support, defined as the minimal set of vertices required to represent the state, directly correlates with the state’s separability; states with Supports concentrated in a lower-dimensional subspace are more likely to be separable or possess limited entanglement. Analyzing the Support’s geometry – its size, dimensionality, and distribution within the n-cube – allows for the determination of entanglement characteristics without requiring complete state reconstruction, offering an alternative to traditional methods like full state tomography which scale exponentially with system size.
Atomically-precise states (APS) and position-dependent states (PDS) exhibit varying degrees of separability directly correlated to their structural composition. APS, characterized by localized atomic configurations, can be separable or entangled depending on the distribution of atomic correlations within the state. Similarly, PDS, where the quantum state is dependent on the spatial location of constituent particles, demonstrate that increased spatial separation generally leads to decreased entanglement, although specific functional dependencies dictate the precise degree of separability. Analysis reveals that the number of independent spatial or atomic components within these states directly impacts the complexity of entanglement, allowing for prediction of separability without full state reconstruction.
Assessing entanglement via the geometrical representation of quantum states offers a substantial computational advantage over traditional methods like full-state tomography. Full-state tomography requires a computational complexity scaling as O(2^{2.5n}), where ‘n’ represents the number of qubits. In contrast, the described approach, leveraging state structure and its n-cube Support, achieves a complexity of O(nk), where ‘k’ defines a parameter related to the state’s structure. This reduction in complexity allows for a significantly faster determination of entanglement properties, particularly as the number of qubits increases, making it a more feasible option for larger quantum systems.
Defining Separability: Amplitude-Dependent States and Beyond
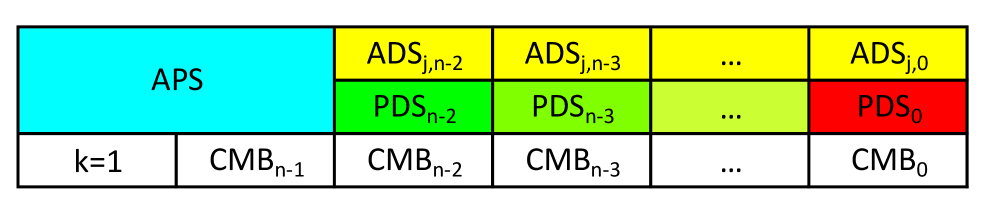
Amplitude-Dependent Separability (ADS) states function as a critical benchmark in quantum information science due to their capacity for precise control over the degree of separability exhibited by a quantum state. These states are specifically engineered such that their separability is not a fixed property, but rather varies depending on the amplitudes of the constituent quantum components. This controllability is achieved through careful manipulation of state preparation, allowing researchers to systematically investigate the transition between separable and entangled states. By defining states with precisely known amplitude-dependent separability characteristics, researchers can validate theoretical models and assess the performance of entanglement detection methods, ultimately providing a standardized framework for quantifying and manipulating quantum separability.
Schmidt Decomposition is a mathematical technique used to represent a quantum state as a sum of product states, each weighted by a singular value. This decomposition is crucial for characterizing amplitude-dependent separability because it reveals the rank of the density matrix representing the bipartite quantum state. The singular values, \sigma_i, obtained from the decomposition directly quantify the contribution of each product state to the overall state. Critically, these singular values are directly linked to the entanglement entropy, specifically the von Neumann entropy S = -Tr(\rho \log_2 \rho), where ρ is the density matrix. A state with only one singular value is necessarily separable, while multiple non-zero singular values indicate entanglement. The number of significant singular values – those above a defined threshold – directly corresponds to the minimal number of entangled pairs needed to represent the state, providing a quantifiable measure of its entanglement and separability.
The construction of guaranteed fully inseparable states is achievable through the identification of “forbidden” support sizes – specific numbers of qubits for which a separable state cannot exist given the system’s constraints. This technique allows for a reduction in the computational complexity of determining separability; instead of analyzing the full n-qubit Hilbert space, the problem is effectively reduced to an n-c-qubit space, where c represents the number of qubits exhibiting localized, classical behavior. By precluding certain support sizes as potential hosts for separable states, the search space for proving inseparability is significantly constrained, leading to more efficient algorithms and analyses.
Constructing Entanglement: Quantum Gates and Multi-Qubit States
The generation of highly entangled states, including Greenberger-Horne-Zeilinger (GHZ) states, is fundamentally achieved through the application of single- and multi-qubit quantum gates. Specifically, the |0\rangle and |1\rangle states are manipulated using the Hadamard gate, which creates superpositions. These superposed qubits are then acted upon by the Controlled-NOT (CNOT) gate, enabling entanglement between them. By applying a sequence of Hadamard and CNOT gates to multiple qubits initialized in the |0\rangle state, a GHZ state – a maximally entangled state where all qubits are correlated – can be reliably constructed. The specific arrangement and number of these gates determine the resulting entangled state and its properties.
The creation of multi-qubit entanglement is achieved by sequentially applying single- and multi-qubit quantum gates, with the tensor product operation serving as the mathematical framework for describing the resulting combined state. Specifically, the tensor product \otimes defines the state of a multi-qubit system given the individual qubit states after each gate application. For example, applying a Hadamard gate to a qubit in the |0⟩ state yields (|0⟩ + |1⟩)/\sqrt{2} . Subsequent application of a Controlled-NOT (CNOT) gate, utilizing this first qubit as control and a second qubit initialized to |0⟩ , results in an entangled Bell state defined by the tensor product \frac{1}{\sqrt{2}} (|00⟩ + |11⟩) . This process is extensible to larger numbers of qubits, allowing for the construction of more complex entangled states like GHZ states through repeated application of gates and tensor product operations.
The ability to construct and manipulate multi-qubit entangled states is a foundational requirement for practical quantum information processing. Quantum algorithms, including those designed for simulation, optimization, and cryptography, rely on the creation of specific entangled states as initial resources or intermediate steps in computation. Scalable quantum computers necessitate techniques for reliably generating and maintaining entanglement across a large number of qubits, as entanglement is fragile and susceptible to decoherence. Furthermore, the fidelity of these constructed states directly impacts the accuracy and reliability of quantum computations; therefore, advancements in entanglement construction are crucial for overcoming current limitations in quantum technology and achieving fault-tolerant quantum computation.
Quantum Information: Towards Practical Applications
Combinatorial Quantum Information offers a fundamentally new toolkit for dissecting the behavior of intricate quantum systems, moving beyond traditional approaches often limited by exponential scaling. This field leverages the principles of combinatorics – the study of arrangements and combinations – to map and analyze the vast Hilbert spaces that describe quantum states. By focusing on the underlying symmetries and structures within these spaces, researchers can drastically reduce the computational burden of simulating and understanding quantum phenomena. Instead of tracking every possible quantum state, combinatorial methods identify and exploit patterns, enabling the efficient calculation of key properties and the prediction of system behavior. This is achieved through techniques like tensor networks and graphical models, which represent quantum states as networks of interconnected components, allowing for the simplification of complex calculations and the effective study of many-body quantum systems – a crucial step towards realizing practical quantum technologies.
The progression of Quantum Information Processing hinges critically on the development of robust analytical techniques, and combinatorial methods offer precisely this advancement. These approaches enable researchers to dissect and understand the behavior of increasingly complex quantum systems – a prerequisite for building practical quantum technologies. By providing tools to manage and interpret quantum states, these techniques facilitate the design of more efficient quantum algorithms and error correction schemes. Ultimately, this enhanced analytical capability is not merely a theoretical exercise; it directly addresses the substantial engineering challenges inherent in scaling quantum systems from a few qubits to the millions required for impactful computation, bringing the promise of quantum technologies – from drug discovery to materials science – closer to realization.
The progression towards practical quantum technologies hinges on effectively translating theoretical advancements into tangible results, a process now significantly accelerated by combinatorial quantum information techniques. Historically, the computational demands of analyzing even moderately complex quantum systems presented a substantial barrier; however, recent innovations have dramatically reduced this complexity to O(nk), where ‘n’ represents the number of quantum particles and ‘k’ a much smaller parameter characterizing entanglement. This reduction isn’t merely an incremental improvement; it unlocks the possibility of simulating and controlling systems previously considered intractable, paving the way for breakthroughs in areas like materials science, drug discovery, and secure communication. By streamlining computational processes, researchers can now focus on designing and implementing quantum algorithms with greater efficiency, fostering a future where the promise of quantum computation becomes a widespread reality.
The pursuit of classifying quantum states, as detailed in this work concerning qubit separability, echoes a fundamental tenet of rigorous inquiry. This research, by introducing the support taxonomy and offering a computationally efficient alternative to Schmidt decomposition, doesn’t claim to prove separability, but rather offers a systematic method for disproving non-separability. As Wilhelm Röntgen stated, “I have made the discovery myself, and I am not going to let anyone steal it.” This sentiment mirrors the meticulous process of refining understanding through repeated testing and challenging assumptions, ultimately moving closer to a robust depiction of quantum reality. The focus on variance within the Boolean cube geometry-a method to identify outliers in quantum states-highlights the importance of acknowledging the complexities beyond simplified averages.
What’s Next?
The present work offers a geometrical shortcut – a ‘support taxonomy’ – for navigating the treacherous terrain of quantum separability. It is, of course, a compromise. Any classification scheme, however elegant, merely organizes ignorance. The Boolean cube provides a convenient, if ultimately limited, framework. One suspects the true structure of entanglement, if it exists as a neatly defined thing at all, will prove far more…fractal. The efficiency gained through this approach buys time, certainly, but time for what? For more elaborate simulations, or for a fundamental rethinking of what ‘separable’ even means in the face of genuinely complex quantum states?
The reliance on Schmidt decomposition, even as a benchmark, highlights a persistent anxiety within the field. The speed-up achieved is valuable, but it’s crucial to ask: optimal for whom? For those seeking incremental progress on existing architectures? Or for those daring to envision quantum information processing beyond the limitations of current models? The taxonomy itself begs expansion. What novel insights emerge when applied to higher-dimensional systems, or to states incorporating temporal correlations?
Ultimately, this work serves as a useful tool – a sophisticated map, if you will. But a map is not the territory. The real challenge remains: to move beyond classifying states, and to harness the peculiar, non-classical correlations that define them. The pursuit of ‘quantum advantage’ demands more than just faster computation; it requires a deeper understanding of the very nature of quantum reality, and a willingness to abandon cherished assumptions when the data – inevitably – contradicts them.
Original article: https://arxiv.org/pdf/2601.15364.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Unlock the Mines in Cookie Run: Kingdom
- Assassin’s Creed Black Flag Remake: What Happens in Mary Read’s Cut Content
- Upload Labs: Beginner Tips & Tricks
- Jujutsu Kaisen: Divine General Mahoraga Vs Dabura, Explained
- Jujutsu Kaisen Modulo Chapter 18 Preview: Rika And Tsurugi’s Full Power
- Mario’s Voice Actor Debunks ‘Weird Online Narrative’ About Nintendo Directs
- The Winter Floating Festival Event Puzzles In DDV
- How to Use the X-Ray in Quarantine Zone The Last Check
- ALGS Championship 2026—Teams, Schedule, and Where to Watch
- Top 8 UFC 5 Perks Every Fighter Should Use
2026-01-23 07:41