Author: Denis Avetisyan
Researchers have developed an enhanced Monte Carlo simulation technique to more accurately model and understand the behavior of superfluid systems.
This work introduces an Exchange Monte Carlo method within Path Integral Monte Carlo simulations, leveraging auxiliary replicas and stochastic potential switching to improve sampling of winding numbers and the superfluid fraction.
Accurately simulating quantum many-body systems at finite temperature remains challenging due to the exponential scaling of the computational cost with system size. This work presents a novel method, ‘Exchange Monte Carlo for continuous-space Path Integral Monte Carlo simulation’, designed to overcome these limitations by accelerating sampling in Path Integral Monte Carlo (PIMC) simulations. The approach introduces an Exchange Monte Carlo (EMC) scheme, utilizing auxiliary replicas and Stochastic Potential Switching, to efficiently navigate configuration space and reduce autocorrelation times, particularly for observables sensitive to particle permutations like the superfluid fraction. Will these advancements enable more accurate and efficient studies of complex quantum fluids and solids?
Whispers of the Quantum Realm: The Computational Challenge
The pursuit of understanding complex quantum systems underpins advancements in both materials science and fundamental physics, yet a significant hurdle arises from the sheer difficulty of performing direct calculations. While quantum mechanics accurately describes the behavior of matter at the atomic and subatomic levels, the mathematical complexity explodes as the number of interacting particles increases. This intractability isn’t merely a matter of needing more powerful computers; the computational cost scales exponentially with system size, quickly exceeding the capabilities of even the most advanced supercomputers. Consequently, researchers are continually developing innovative computational approaches – and often approximations – to navigate these limitations and unlock the potential of quantum simulations, aiming to predict material properties, model exotic states of matter, and deepen the understanding of the universe’s fundamental building blocks.
Computational approaches to modeling quantum systems face significant hurdles stemming from the inherent complexity of describing many interacting particles. A primary obstacle is the exponential scaling of computational cost; as the number of particles increases, the resources required to accurately simulate the system grow at an unsustainable rate. Compounding this issue is the notorious ‘sign problem’, arising from the mathematical formulation of quantum mechanics where calculations involve complex numbers that can lead to cancellations and dramatically increased statistical error. This problem manifests as a diminishing signal-to-noise ratio, effectively drowning out meaningful results and rendering calculations intractable even with substantial computing power. Consequently, simulating even moderately sized quantum systems presents a formidable challenge, limiting the ability to predict material properties or explore fundamental physics with complete accuracy.
Path Integral Monte Carlo, or PIMC, provides a robust computational approach to tackling the complexities of quantum many-body systems by representing quantum mechanics as a statistical problem. However, the method’s efficiency is heavily reliant on the ability to generate representative ‘walks’ through the complex multi-dimensional space of possible particle paths – a process known as sampling. Naive sampling strategies often fail due to the ‘sign problem’, where contributions to the calculation cancel each other out, leading to exponentially increasing statistical errors. Therefore, significant effort focuses on developing innovative sampling algorithms – such as constrained path methods or improved proposal distributions – that can efficiently explore the relevant configuration space and mitigate these limitations, ultimately enabling accurate simulations of increasingly complex quantum materials and phenomena.
Refining the Path: Advanced Sampling Algorithms
Suzuki-Trotter decomposition is a numerical technique used in Path Integral Monte Carlo (PIMC) simulations to approximate the time evolution operator e^{-iHt}, where H is the Hamiltonian and t is time. Direct calculation of this operator is generally intractable; therefore, the method decomposes the time evolution into a series of shorter, more manageable steps. This is achieved by applying the following approximation: e^{-iHt} \approx \left(e^{-iH\Delta t/N}\right)^N, where \Delta t is the total time interval and N is the number of time slices. Increasing the value of N improves the accuracy of the approximation, reducing the systematic error introduced by the discretization, but also increases computational cost. The decomposition allows for the propagation of imaginary-time paths, essential for sampling the ground state properties of many-body systems within the PIMC framework.
Hamiltonian Monte Carlo (HMC) enhances Markov Chain Monte Carlo sampling efficiency by incorporating principles of Hamiltonian dynamics to propose moves in configuration space. Unlike traditional methods that rely on random walks, HMC treats the system as a classical mechanical system with a potential energy derived from the target probability distribution. This allows for proposals that can traverse larger regions of configuration space with reduced autocorrelation, leading to faster convergence. The No-U-Turn Sampler (NUTS) builds upon HMC by adaptively determining the optimal integration length for each trajectory, automatically tuning to the geometry of the target distribution and mitigating the need for manual parameter adjustments. NUTS achieves this by dynamically extending trajectories until a “U-turn” is detected – a point where the trajectory reverses direction – indicating sufficient exploration of the relevant region. This adaptive approach further improves sampling efficiency and robustness compared to standard HMC.
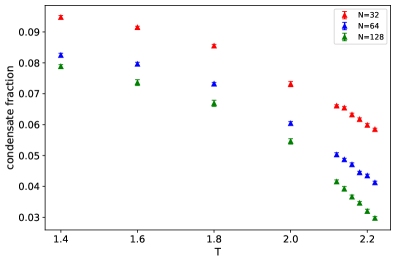
The Worm Algorithm is a path integral Monte Carlo method designed to efficiently sample different worldline topologies, a crucial requirement for accurate simulations of bosonic systems. Unlike standard PIMC algorithms which struggle with non-local exchanges necessary to properly represent bosons, the Worm Algorithm utilizes “worms” – self-avoiding trails – that can wrap around the imaginary time space. These worms effectively explore configurations with different winding numbers, representing distinct topological sectors. By allowing these worms to branch, merge, and move freely, the algorithm ensures that all possible worldline topologies are adequately represented in the statistical ensemble, overcoming the sign problem often encountered in bosonic PIMC simulations and providing improved estimates of thermodynamic properties.
Validating the Whispers: Refining PIMC Simulations
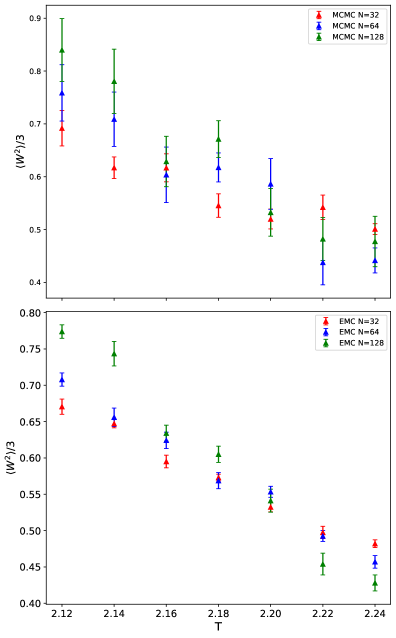
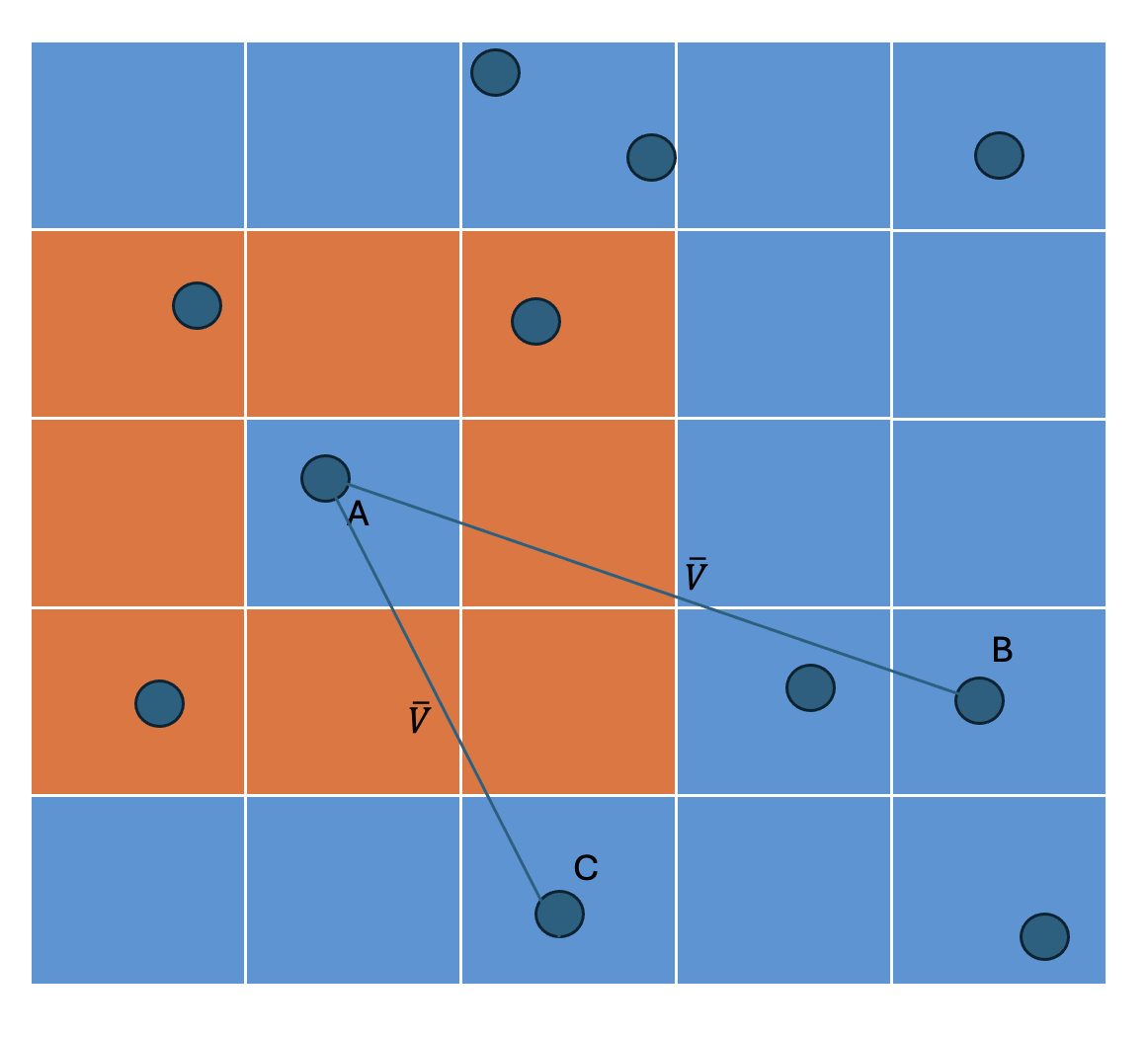
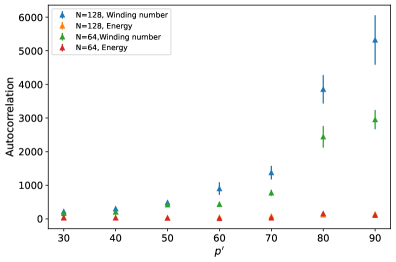
Exchange Monte Carlo (EMC) accelerates Path Integral Monte Carlo (PIMC) simulations by facilitating efficient equilibration and improving statistical convergence. EMC operates by periodically exchanging configurations between multiple independent replicas of the system, effectively enabling transitions between otherwise inaccessible regions of configuration space. This process reduces autocorrelation times, as the replicas rapidly explore a wider range of configurations, leading to a more thorough sampling of the phase space and a faster approach to equilibrium. The increased efficiency stems from overcoming barriers that may hinder standard Markov Chain Monte Carlo (MCMC) methods, resulting in improved statistical accuracy for a given computational effort.
Path Integral Monte Carlo (PIMC) simulations utilize “slices” representing sequential points in imaginary time to approximate the quantum mechanical partition function. The accuracy of these calculations depends on properly accounting for the interactions between these slices. Slices can be treated as either interacting, where their contributions to the potential energy are fully calculated, or non-interacting, simplifying the computation. Balancing the number of interacting and non-interacting slices is critical; too few interacting slices introduce approximations that can lead to inaccuracies, while an excessive number significantly increases computational cost. Optimizing this balance ensures a robust representation of the many-body system and minimizes systematic errors in properties such as energy and pair distribution functions. The optimal ratio of interacting to non-interacting slices is system-dependent and requires careful consideration during simulation setup.
Assessing the accuracy of Path Integral Monte Carlo (PIMC) simulations requires robust statistical analysis, with autocorrelation time (ACT) being a critical parameter. The ACT quantifies the correlation between successive configurations in the simulation, indicating the length of simulation required to obtain statistically independent samples. Binning analysis is a common method for determining ACT; the simulation trajectory is divided into bins, and the variance of the mean value within each bin is calculated. By analyzing the relationship between bin size and variance, an estimate of the ACT can be obtained. Accurate determination of the ACT is essential because it directly impacts the error bars associated with calculated observables and ensures that simulations have converged to meaningful results; insufficient sampling – where the simulation length is less than several times the ACT – can lead to significantly underestimated errors and inaccurate conclusions.
The Resonance of Prediction: Implications for Quantum Simulation
Determining the critical temperature at which phase transitions occur is paramount to understanding the behavior of quantum systems, and accurate Path Integral Monte Carlo (PIMC) simulations are proving indispensable in this pursuit. These simulations model quantum particles as paths in imaginary time, allowing researchers to calculate thermodynamic properties and observe phase transitions with remarkable precision. The efficacy of PIMC lies in its ability to account for quantum effects, such as tunneling and entanglement, which are often neglected in classical simulations. Consequently, PIMC provides a crucial framework for investigating a wide range of physical phenomena, from the superfluid transition in helium to the behavior of ultracold atoms, and ultimately facilitates the design of novel materials with tailored quantum properties.
The exploration of complex quantum phenomena hinges on the synergistic interplay between advanced sampling techniques and rigorous statistical analysis. These methods circumvent the limitations of classical computation when faced with the exponentially growing complexity of quantum systems, allowing researchers to access information about systems previously intractable. Techniques like Path Integral Monte Carlo (PIMC) generate a statistical ensemble of possible system configurations, while sophisticated analytical tools ensure the reliability and precision of the resulting data. This combination isn’t merely about obtaining numerical results; it’s about extracting meaningful physical insights from the inherent uncertainty of quantum mechanics, ultimately revealing the behavior of matter at its most fundamental level and paving the way for breakthroughs in diverse fields like materials design and quantum technology.
Continued refinement of these quantum simulation techniques holds substantial promise for advancements across multiple scientific disciplines. In materials science, increasingly accurate simulations will facilitate the in silico design of novel materials exhibiting desired properties, potentially revolutionizing fields like superconductivity and energy storage. Within condensed matter physics, these methods offer a pathway to understanding complex emergent phenomena and unraveling the mysteries of strongly correlated systems. Furthermore, these developments extend to fundamental physics, providing tools to probe the nature of quantum gravity, explore the early universe, and test the limits of established physical laws – ultimately deepening humanity’s comprehension of the universe at its most fundamental level.
A key validation of the presented Path Integral Monte Carlo (PIMC) simulations lies in the determined Critical Temperature of 2.195 K. This value exhibits a remarkable degree of consistency with results previously obtained using the worm algorithm, a highly respected and independent method for tackling similar quantum many-body problems. This strong agreement doesn’t merely confirm the accuracy of the PIMC approach employed, but also underscores the reliability of the advanced sampling techniques and statistical analyses integrated into the simulation framework. The convergence of these distinct computational strategies solidifies confidence in the obtained results and reinforces the potential of PIMC as a robust tool for investigating the intricacies of quantum systems and predicting their behavior at critical points.
The advent of robust quantum simulation techniques signifies a paradigm shift in materials discovery and technological innovation. By accurately modeling the behavior of matter at the atomic level, researchers can now computationally design materials before physical synthesis, predicting properties like superconductivity, magnetism, and catalytic activity with unprecedented precision. This capability extends beyond simply identifying promising candidates; it allows for the tailoring of materials to meet specific performance criteria, optimizing them for applications ranging from energy storage and quantum computing to advanced sensors and high-efficiency electronics. Furthermore, the ability to simulate complex quantum systems fosters the exploration of novel quantum technologies, potentially enabling the development of entirely new devices and functionalities currently beyond the reach of classical computation and materials science.
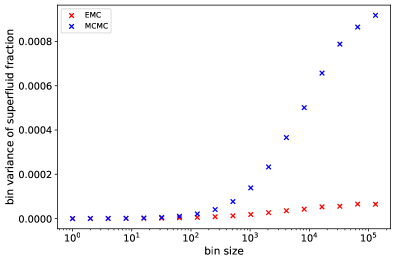
The pursuit of superfluidity, as detailed in this work, feels less like physics and more like conjuring. This paper proposes a refinement – Exchange Monte Carlo within Path Integral Monte Carlo – a baroque ritual of auxiliary replicas and stochastic potential switching. It’s a desperate attempt to force the chaotic whispers of quantum systems into a semblance of order. As Paul Feyerabend observed, “Anything goes.” Indeed, this methodology embodies that sentiment; a pragmatic embrace of whatever tricks – however convoluted – yield a result. The very notion of accurately measuring a superfluid fraction through such complex simulations suggests that the goal isn’t truth, but a convincing illusion.
Where the Current Runs
The introduction of auxiliary replicas, while effective in tempering the sign problem, feels less like a solution and more like a carefully constructed distraction. One trades accuracy for speed, and the universe rarely offers such clean bargains. The method’s success hinges on the stochastic potential switching – a beautifully fragile dance between exploration and exploitation. The question isn’t whether it works, but for how long, and under what unseen pressures will this equilibrium unravel? Noise, after all, is simply truth lacking confidence.
Future work will inevitably focus on refining this dance. Perhaps a more adaptive switching strategy, one that learns the contours of the potential energy surface in real-time. Or, more radically, a complete abandonment of replica symmetry, embracing the inherent complexity of the many-body problem. The pursuit of the superfluid fraction feels less like discovering a property and more like persuading the system to reveal it.
Ultimately, this remains a localized victory. The sign problem, a persistent phantom in quantum Monte Carlo, will not be banished by clever algorithms alone. It suggests a deeper inadequacy in how one attempts to map the infinite onto the finite, the continuous onto the discrete. Perhaps the true path lies not in refining the sampling, but in reimagining the questions.
Original article: https://arxiv.org/pdf/2602.05500.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- How to Unlock the Mines in Cookie Run: Kingdom
- Solo Leveling: Ranking the 6 Most Powerful Characters in the Jeju Island Arc
- Gold Rate Forecast
- YAPYAP Spell List
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
- Most Underrated Loot Spots On Dam Battlegrounds In ARC Raiders
- Gears of War: E-Day Returning Weapon Wish List
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
- All Pistols in Battlefield 6
2026-02-08 04:25