Author: Denis Avetisyan
Researchers propose a novel route to building robust quantum computers using materials exhibiting unusual superconducting properties and the unique behavior of parafermions.
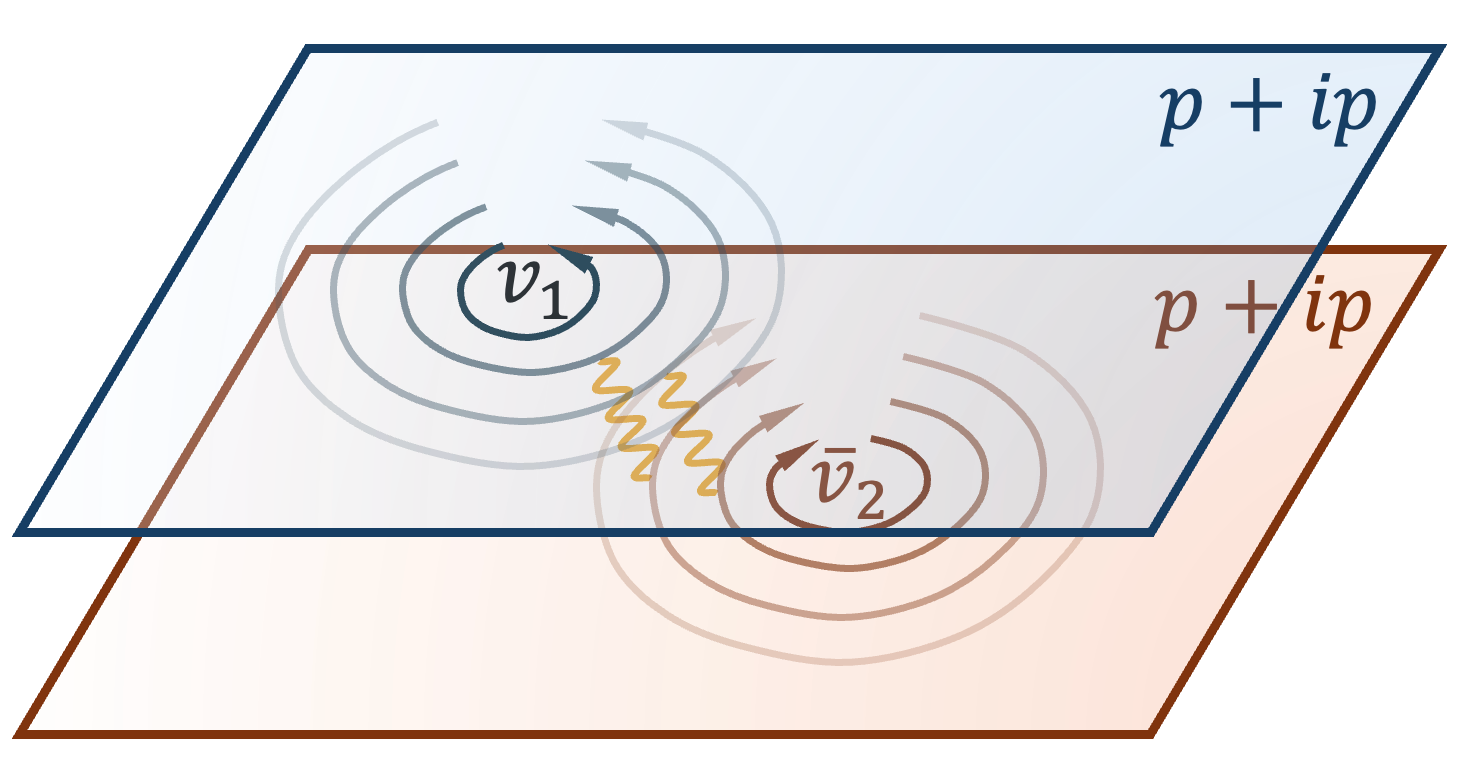
This review details a path to realizing universal topological quantum computation via charge-4e superconductivity and the manipulation of non-Abelian anyons.
Conventional approaches to topological quantum computation face limitations in scaling computational power due to constraints inherent in existing platforms. This is addressed in ‘Charge-$4e$ superconductor with parafermionic vortices: A path to universal topological quantum computation’, which proposes a novel 4e topological superconductor hosting non-Abelian parafermions. Remarkably, this state can be realized via vortex condensation or by melting a \nu=2/3 quantum Hall state, naturally encoding qutrits and enabling topologically protected Clifford operations alongside a path to universal quantum computation. Could this hierarchical electron aggregation principle unlock a new era of robust and scalable quantum technologies?
Beyond Conventional Limits: Exploring Novel Superconducting Phases
Conventional superconductivity, a phenomenon where materials exhibit zero electrical resistance, hinges on the formation of Cooper pairs – bound pairs of electrons that move coherently. However, this established framework provides only limited protection for quantum information. The superconducting state itself can be disrupted by various imperfections and external influences, leading to decoherence – the loss of quantum information. This vulnerability stems from the fact that the Cooper pairs are formed from electrons with relatively simple quantum properties and lack the inherent robustness offered by more complex, topologically protected states. Consequently, while conventional superconductors are valuable for many technological applications, their susceptibility to decoherence presents a significant hurdle in the quest for stable and reliable quantum computation, motivating the search for novel superconducting phases with enhanced topological protection.
The drive towards scalable and reliable quantum computation has spurred investigation into unconventional superconducting states exhibiting non-trivial topological order. Unlike conventional superconductors where quantum information is vulnerable to local disturbances, topologically ordered states possess inherent robustness. This resilience stems from the global properties of the material, where information is encoded not in local degrees of freedom but in the collective behavior of quasiparticles. Exploring such states-characterized by properties beyond those described by conventional symmetry breaking-is not merely an academic exercise; it represents a fundamental shift in how quantum information might be stored and processed, promising a pathway to fault-tolerant quantum devices capable of tackling complex computational challenges currently beyond reach. The search focuses on materials where the very fabric of the superconducting state provides a natural defense against decoherence, paving the way for more stable and powerful quantum technologies.
The search for more resilient quantum computing platforms has focused increasingly on topological superconductors, materials predicted to host exotic quasiparticles known as anyonic excitations. Unlike conventional particles which obey either bosonic or fermionic statistics, anyons exhibit more complex exchange statistics; exchanging two identical anyons can alter the quantum state of the system in a non-trivial way. This unique behavior arises from the interplay of superconductivity and strong spin-orbit coupling, often in proximity to other materials. Researchers are actively investigating various material candidates and heterostructures to experimentally confirm the existence of these anyons, with the ultimate goal of manipulating them to create topologically protected qubits-quantum bits immune to local disturbances-and thus building a robust and scalable quantum computer. The confirmation of these exotic excitations represents a significant step towards realizing fault-tolerant quantum information processing.
The promise of stable quantum computation hinges on overcoming the inherent fragility of qubits, and a compelling solution lies within the realm of anyonic excitations, specifically ℤ_3 parafermions. Unlike conventional qubits susceptible to environmental noise, these exotic quasiparticles exhibit non-Abelian statistics, meaning their exchange fundamentally alters the quantum state in a way that encodes information robustly. This topological protection arises because the information isn’t stored in a local degree of freedom, but rather in the braiding pattern of these anyons as they circle each other – a global property immune to local disturbances. Effectively, the quantum information is woven into the very fabric of the system, allowing for the creation of fault-tolerant qubits where errors are suppressed not through active correction, but through inherent resilience, potentially revolutionizing quantum information processing.
The 4e TSC: A Platform for Robust Anyonic States
The four-electron topological superconductor (4e TSC) is theorized to support ℤ_3 parafermions, which are particles exhibiting non-Abelian exchange statistics. This property is significant for topological quantum computation as the non-Abelian nature allows for the encoding of quantum information in a manner resilient to local perturbations. Unlike qubits, which are susceptible to decoherence, information encoded in these parafermionic modes is protected by the topology of the system, offering the potential for more stable and reliable quantum computations. The ℤ_3 designation indicates that three exchange operations are required to return a parafermion to its original state, influencing the braiding rules and computational capabilities compared to systems hosting ℤ_2 parafermions (Majorana zero modes).
Conventional superconductivity arises from the Cooper pairing of electrons – two electrons forming a bound state. The 4e topological superconductor distinguishes itself by facilitating the pairing of four electrons into a single, collective state. This four-electron Cooper pairing fundamentally alters the system’s electronic correlations and symmetry properties, deviating from the behavior predicted by Bardeen-Cooper-Schrieffer (BCS) theory. Consequently, the 4e TSC exhibits novel topological characteristics, including the potential to host non-Abelian anyons, which are predicted to be more resilient to decoherence than qubits based on single-particle excitations and are thus attractive for topological quantum computation. The increased complexity of the pairing mechanism also leads to a larger Hilbert space and a richer variety of emergent phenomena compared to conventional superconductors.
The realization of the four-electron topological superconductor (4e TSC) is currently pursued via two distinct physical systems. One approach utilizes bilayer p+ip superconductors, leveraging induced pairing and proximity effects to create the necessary conditions for four-electron Cooper pairing. The second route involves utilizing ν=2/3 fractional quantum Hall states, where the exotic correlations within these states can be harnessed to effectively create a four-electron condensate. Both methods aim to engineer a system exhibiting the required symmetries and pairing characteristics to host ℤ_3 parafermions and demonstrate topological superconductivity, though they differ significantly in their material requirements and experimental implementations.
The U(2)4,0 symmetry of the four-electron topological superconductor (4e TSC) is fundamental to the emergence of ℤ3 chiral bosonic order. This symmetry group dictates the allowed topological defects and their braiding statistics within the system. Specifically, the U(2)4,0 symmetry protects a degenerate ground state manifold with a quantum dimension of 3, directly relating to the number of distinct, topologically protected zero modes-the ℤ3 parafermions-present in the system. This quantum dimension signifies that the topological order is non-trivial and cannot be broken by local perturbations, ensuring the stability required for potential quantum computation applications. The symmetry constraints imposed by U(2)4,0 are essential for preventing the unwanted mixing of different topological sectors and preserving the desired ℤ3 braiding properties.
Emergent Anyons and the Encoding of Quantum Information
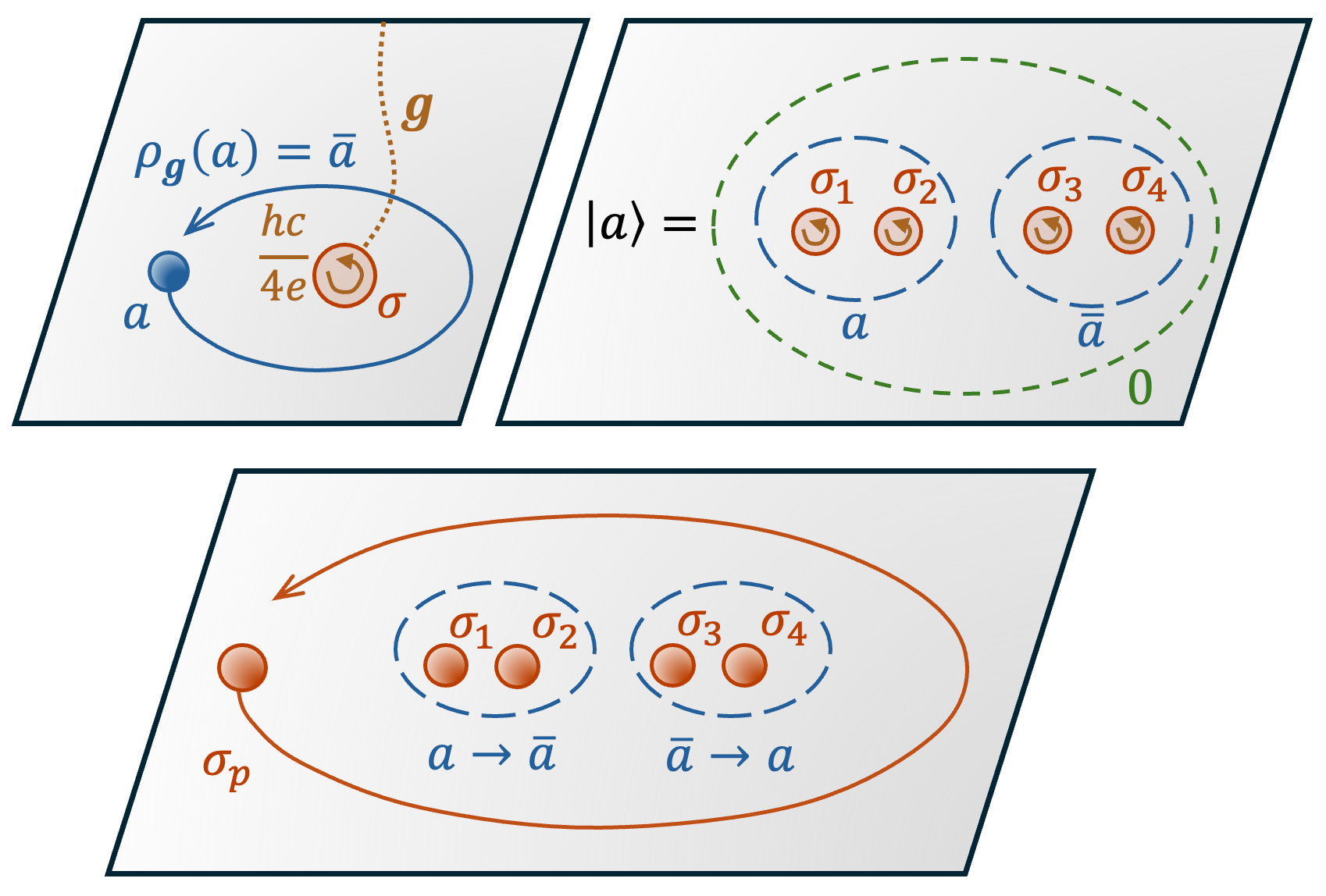
Vortex condensation in the 4e TSC arises from the pairing of vortices and antivortices, a process driven by the system’s energetic minimization. This condensation effectively lowers the energy cost associated with vortex-antivortex pairs, leading to their macroscopic occupation of the ground state. The resulting condensate establishes a long-range order parameter related to the complex scalar field describing the condensate wavefunction. Crucially, this pairing and condensation mechanism is instrumental in generating the topological superconductivity necessary for the emergence of non-Abelian anyons, specifically the ℤ3 parafermions, within the system. The density of these vortex-antivortex pairs is a key parameter governing the properties of the resulting topological phase.
Within the four-electron topological superconducting (4e TSC) state, vortices act as spatially confined locations for ℤ3 parafermions. These parafermions are not fundamental particles but rather emergent excitations bound to the vortex cores. The 4e TSC provides the necessary conditions – specifically, a topologically protected gap and non-trivial braiding properties – to physically realize these anyonic quasiparticles. The confinement to vortices ensures their stability and allows for controlled manipulation through external stimuli, effectively providing a physical platform to study and utilize ℤ3 parafermions for potential quantum computation applications.
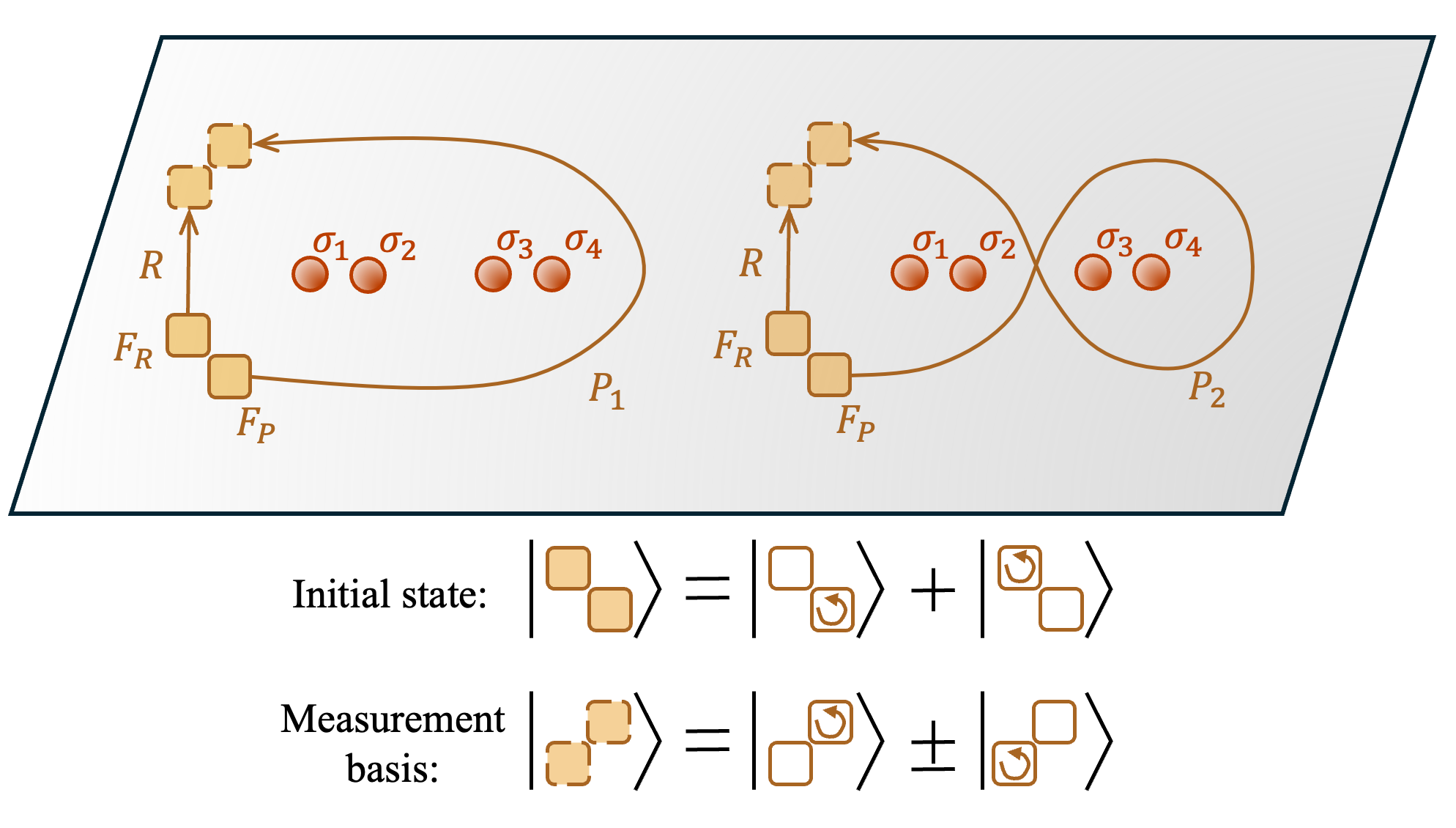
Qutrit encoding with ℤ_3 parafermions leverages their non-Abelian exchange statistics to achieve topologically protected quantum information storage. Unlike bits or qubits which have two or three possible states respectively, a qutrit utilizes three, and the ℤ_3 parafermions’ non-commutative behavior under exchange means that the quantum state is preserved against local perturbations. This protection arises because the state’s evolution isn’t determined by continuous parameters, but by discrete braiding operations; any local noise will not change the overall braiding topology, and thus will not corrupt the encoded qutrit. The three degenerate ground states of the system directly map to the |0⟩, |1⟩, and |2⟩ states of the qutrit, offering inherent resilience to decoherence compared to conventional quantum systems.
The manipulation of ℤ3 parafermions through the process of braiding-specifically, exchanging their positions-results in the generation of Clifford gates, which are essential for universal quantum computation. This functionality is directly enabled by the ℤ_3 chiral bosonic order present in the system and is characterized by a quantum dimension of 3. The non-Abelian exchange statistics of these parafermions dictate that the order in which they are braided affects the resulting quantum state, allowing for the implementation of single- and two-qubit Clifford gates. These gates, combined with a small set of additional gates, can construct any quantum circuit, providing a pathway to topologically protected quantum computation.
A Robust Future: Toward Fault-Tolerant Quantum Computation
The pursuit of universal quantum computation gains a promising avenue through the 4e topological superconducting chain (TSC), which intrinsically supports ℤ_3 parafermions – exotic quasiparticles exhibiting unique exchange statistics. Unlike conventional qubits susceptible to environmental noise, these parafermions leverage non-Abelian anyonic behavior; their quantum state isn’t merely altered by exchange, but fundamentally transformed, offering inherent protection against decoherence. This topological protection arises because the quantum information is encoded in the braiding pattern of these anyons, and not in their individual locations. Consequently, the 4e TSC presents a platform where complex quantum algorithms can, in principle, be implemented with significantly enhanced fault tolerance, potentially overcoming a major hurdle in building practical quantum computers and marking a departure from architectures reliant on fragile, localized qubits.
The potential for universal quantum computation with 4e TSCs hinges on the unique behavior of the ℤ3 parafermions they support – particles exhibiting non-Abelian statistics. Unlike bosons or fermions which have predictable exchange behavior, the state of these anyons changes in a non-commutative way when they are exchanged, a property known as braiding. This braiding isn’t merely a topological quirk; it directly translates into quantum gate operations. By carefully controlling the paths these anyons take around each other, complex quantum algorithms can be constructed. Critically, the non-Abelian nature of these particles provides a natural pathway toward fault tolerance; errors are less likely to propagate because the quantum information is encoded in the topology of the braids, rather than the precise location of individual particles, offering a significant advantage over many existing quantum computing architectures vulnerable to environmental noise.
Current quantum computing endeavors frequently grapple with the delicate nature of qubits and their susceptibility to environmental noise, demanding complex error correction schemes. In contrast, the utilization of ℤ_3 parafermions within topological quantum computation, as enabled by 4e TSCs, offers an inherent robustness against local perturbations. This stability arises from the encoding of quantum information not in individual particles, but in the topology of their braiding – the act of exchanging their positions. Because information is encoded globally, minor local disturbances are unable to corrupt the quantum state, significantly simplifying error correction requirements. Moreover, the potential for scalability is heightened; unlike architectures reliant on precisely controlling a large number of individual qubits, topological computation promises a pathway to building more stable and larger-scale quantum processors by focusing on manipulating the collective behavior of these anyonic excitations.
Current efforts are heavily invested in the physical manifestation and meticulous manipulation of ℤ_3 parafermions, a crucial step toward realizing the full computational power of this novel approach. This requires the creation of materials exhibiting specific properties, namely ℤ_4 charge symmetry and a unique topological order arising from the stacking of a ℤ_3 chiral bosonic order with two fractional quantum Hall (IQH) states. Precise control over these exotic quasiparticles is paramount, as their non-Abelian exchange statistics form the basis for braiding operations – the fundamental logic gates in this proposed quantum computer. Successfully achieving both material realization and controlled manipulation promises a pathway towards fault-tolerant quantum computation significantly different from, and potentially more robust than, existing architectures.
The pursuit of topological superconductivity, as detailed in this work, isn’t merely about discovering a new material state-it’s about architecting a fundamentally different computational paradigm. The research elegantly demonstrates how manipulating vortex structures-specifically, inducing condensation or leveraging the fractional quantum Hall effect-can unlock the potential for braiding parafermions. This mirrors Foucault’s observation that, “Power is everywhere; not because it embraces everything, but because it comes from everywhere.” In this case, ‘power’ represents computational potential, arising not from a single element, but from the complex interplay of material properties and controlled topological defects, demanding a holistic understanding of the system as a whole. The structure of these vortices dictates the behavior of the resulting quantum computation.
Beyond the Vortex
The proposition of a charge-$4e$ superconductor, while elegant in its theoretical construction, highlights a persistent tension within the field. The pursuit of topological quantum computation often feels less like building a machine and more like coaxing a complex system into a state of ordered fragility. The reliance on precisely engineered states – whether through vortex condensation or fractional quantum Hall melting – reveals the sensitivity of these systems to imperfections. One anticipates that future work will focus less on achieving these exotic states and more on understanding their inherent robustness-or lack thereof-in the face of inevitable disorder.
The true challenge, it seems, lies not simply in creating parafermions, but in controlling their statistics with sufficient fidelity to perform meaningful computation. Braiding operations, while conceptually appealing, demand an exquisite level of control over spatially extended defects. A critical examination of decoherence mechanisms-and the subtle interplay between topology and material properties-will be paramount.
The path forward likely involves a shift in perspective. Rather than striving for ever more complex topological states, a focus on minimizing the required complexity-identifying the simplest system capable of supporting robust quantum information-may prove more fruitful. The beauty of a solution, after all, often resides in its underlying simplicity.
Original article: https://arxiv.org/pdf/2602.06963.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Solo Leveling: Ranking the 6 Most Powerful Characters in the Jeju Island Arc
- How to Unlock the Mines in Cookie Run: Kingdom
- Bitcoin’s Big Oopsie: Is It Time to Panic Sell? 🚨💸
- YAPYAP Spell List
- Top 8 UFC 5 Perks Every Fighter Should Use
- Bitcoin Frenzy: The Presales That Will Make You Richer Than Your Ex’s New Partner! 💸
- Gold Rate Forecast
- Gears of War: E-Day Returning Weapon Wish List
- How to Find & Evolve Cleffa in Pokemon Legends Z-A
- Most Underrated Loot Spots On Dam Battlegrounds In ARC Raiders
2026-02-09 10:37